1. Introduction
To date, no mathematical correlation exists in the laws of mechanics that relates orbital and rotational motions, despite this effect being ubiquitous in nature. I, therefore, investigated whether a physical correlation exists between these motions, and if it does, then the derivation of its mathematical expression.
In this study, I investigated noninertial systems to better understand the response of rigid bodies subjected to simultaneous noncoaxial rotations. As a result, I proposed hypotheses that require extending my studies to field theory in order to explain the dynamics of such bodies.
The superposition of simultaneous motions was discussed by Galileo [1] to explain the path of a canyon ball. Understanding the superposition of fields caused by torques is important, and I shall refer to the superposition of the velocity fields generated in these cases as “coupling.”
I analyzed the motion of objects subjected to multiple rotations, such as a spinning top, a boomerang, a hoop, and several other objects whose peculiar behavior is intriguing. I believe that my conclusions modify the foundations of rational dynamics and incorporate new criteria of great impact and significance.
2. Experiments and Mathematical Simulation
I investigated how objects respond when subjected to different simultaneous accelerations by applying noncoaxial rotations. In other words, I investigated the motion of a gyroscope, spinning top, or boomerang to determine whether it can be described by the classical mechanics or it corresponds to laws of nature not yet formulated.
To clarify these questions, I performed several experiments that eventually indicate that mathematical formulation should use field theory and consider the concept of dynamics interactions. This implies that the generated dynamics fields interact to cause paths that correspond to some laws of physics that are not yet formulated.
My initial experiments motivated me to establish a dynamics hypothesis stating that under conditions of simultaneous noncoaxial rotations, an object follows a closed path (i.e., orbital motion) without requiring a centripetal force [2,3] and maintains its rotation about its initial axis. By numerical simulation, I confirmed that an object traces a closed path similar to the orbit of a body in space subjected to a centripetal force. However, no such centripetal force existed in my simulation.
Therefore, I was confronted with the challenge of reproducing such a path experimentally.
Watch the video by clicking on the Figure 1 or in this direction: http://dl.dropbox.com/u/48524938/VTS_Ingles.mov
3. Final Tests: Prototype I
Because performing tests in space is difficult and expensive, my tests were conducted in water. I designed a

Figure 1. Theory of dynamic interactions: video illustrating experimental tests.
cylinder or “submarine” driven by a stern-mounted propeller that translated and simultaneously forced the prototype to rotate about its longitudinal axis. The prototype also experienced torque because of its weight and upward buoyancy, both of which acted perpendicular to its longitudinal axis (i.e., its axis of rotation). I experimented using two different prototypes: one with fixed torque (prototype I) and another with variable torque (prototype II; see next section).
For a flat disk rotating about its axis of symmetry (Figure 2), velocity fields due to the rotation of the disk can be identified. For each portion of the disk, the tangential velocity is given by the following equation:
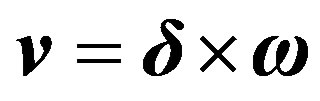 (1)
(1)
with
 : Vector with distance from the particle to the rotation axis.
: Vector with distance from the particle to the rotation axis.
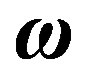 : Rotation speed of the disc.
: Rotation speed of the disc.
Note that d is also the circumference ratio (Figure 2) or the geometric position of the particles whose dynamic state is being analyzed and that are equidistant from the rotation axis.
Therefore, all particles situated at the given radial position have the same tangential velocity but move in different directions, as already demonstrated E. Jouffret [4- 6]. Thus, turning the disk about its axis of symmetry creates a homogeneous and balanced field of velocities (Figure 2).
Prototype I experienced constant-torsion torque because the forces of weight and buoyancy act on different points to generate an imbalance. This torque identified by , which I call the interaction torque, forced the submerged cylinder to turn about a new axis, i.e., the torque axis. However, in line with my hypothesis, I calculated that the cylinder cannot undergo this new turn but can trace a closed circular path.
, which I call the interaction torque, forced the submerged cylinder to turn about a new axis, i.e., the torque axis. However, in line with my hypothesis, I calculated that the cylinder cannot undergo this new turn but can trace a closed circular path.
The velocity of prototype I was remote controlled, and it did not have a rudder or any other steering device. When prototype I was at rest, the torque produced by

Figure 2. Body with angular velocity  about its principal axis. When the body is subjected to a noncoaxial angular velocity
about its principal axis. When the body is subjected to a noncoaxial angular velocity , a nonhomogeneous field of velocities is generated.
, a nonhomogeneous field of velocities is generated.
gravity made the stern sink because prototype I was not balanced. It reached a vertical position with the bow slightly above the water surface. However, once the motor was started and prototype I began rotating on its longitudinal axis, it turned right and initiated a closed path on the water surface with a radius that varied with the translational velocity.
These tests clearly confirmed that prototype I behaved as predicted by the simulation. With no rudder but equipped with its own source of torque about its longitudinal axis, prototype I transformed this torque into an orbital motion, dynamically adding or coupling the linear translational velocity with the centripetal velocity produced by the interaction torque. The resulting path of prototype I was circular despite the absence of external central force that generates such a path. The circular orbit transformed into an elliptical orbit upon modifying the velocity of prototype I. As predicted by my theory, there was clear cause and effect.
The observed behavior can be understood with the help of the field theory mentioned above. Let us analyze the velocity fields that are generated in a section of the prototype. The torque generated by weight and buoyancy generates a second rotation noncoaxial with the existing one on the prototype’s longitudinal axis. This second rotation determines anisotropic fields of velocity and acceleration (see Figure 1 video). However, something exceptional occurs: this new initial velocity distribution is modified when the prototype turns about its longitudinal axis.
When the prototype is turning about its longitudinal symmetry axis, a new velocity distribution is obtained, as seen in the Figure 1 video. The result is that, in line with the analysis of the velocity field, the torque produced by weight and buoyancy generates a new nonhomogeneous velocity field, which rotates the body about an axis different from that about which the external gravitational torque acts. The result is the observed circular path.
Thus, the rotation generated by the gravitational interaction torque does not correspond to the classical laws of mechanics or to vector algebra. In my opinion, after a half turn, the second rotation began about the axis perpendicular to the torque it generated, and not about the axis torque created by the weight and the buoyancy thrust. Once I determined this particular behavior of bodies subjected to simultaneous noncoaxial rotations, which it is defined in classical mechanics as the gyroscopic effect [7,8], I continued to analyze the real behavior of the proto-type.
The new velocity field created by the second rotation is not homogeneous, as is the case for the first rotation, but is an anisotropic velocity field. In line with my hypothesis, this new nonhomogeneous velocity field couples dynamically to the translational velocity field, which implies that both fields add algebraically, while the rotation about the longitudinal axis remains independent, as can be seen in the Figure 1 video.
My main hypothesis is as follows: my experiments confirmed what I detected in the simulation, namely, the translational velocity field of the cylinder couples to the velocity field generated by the torque produced by weight and buoyancy. As a result, prototype I executed a circular path, as can also be observed in the flight of a boomerang or in the path of a spinning top.
4. Prototype II
After concluding the tests with prototype I, I modified it so that it could be steered to the port or starboard by exerting a variable external torque on it. This prototype, named prototype II, was equipped with a mechanism to exert a variable torque by using a pump and two water reservoirs (Figure 3). By transferring the water between the reservoirs, I modified the center of mass of prototype II, which enabled me to sink the bow or stern and thus to change the gravitational interaction torque.
The tests conducted with prototype II completely confirmed my theory. I steered the submarine to the port or starboard, in line with the variation of the gravitational torque. Prototype II could be steered with no rudder according to the dynamic hypothesis of my theory of dynamic interactions.
With the assumption of simultaneous noncoaxial rotations, the rigid body experiences nonhomogeneous velocity fields. These fields generate anisotropic acceleration fields, which can be interpreted as fields of inertial forces created in space through the effect of simultaneous noncoaxial rotations. The result of my experiments confirmed my initial assumption that a correlation can exist

Figure 3. (Color online) Prototype II: design of remote-controlled torpedo submarine.
between rotational and orbital motions such that a body with intrinsic angular momentum [9,10] and translational velocity subjected to a real noncoinciding torque, transforms its dynamic action into a precession, which will generate a flat path with a closed orbit for a constant torque.
5. Equation of Motion
On the basis of the principle of conservation of motion [11], I obtain the equation of motion [12]. Consider an infinitely thin and flat disk with ratio d that experiences a torque M directed along the disk’s symmetry axis (Zaxis). If this torque is instantaneous, it generates a constant angular velocity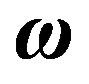 . A second torque
. A second torque , noncoaxial with the former, will generate a new dynamic state, defined in classical mechanics as the gyroscopic effect and attributed to a supposed gyroscopic momentum
, noncoaxial with the former, will generate a new dynamic state, defined in classical mechanics as the gyroscopic effect and attributed to a supposed gyroscopic momentum . Based on the principle of conservation of motion, we can interpret the gyroscopic momentum
. Based on the principle of conservation of motion, we can interpret the gyroscopic momentum  as equivalent to the effect of the external torque
as equivalent to the effect of the external torque  and as being the torque that generates the second rotation, which is noncoaxial with the first. Therefore,
and as being the torque that generates the second rotation, which is noncoaxial with the first. Therefore,
 (2)
(2)
If the torque  is constant in time, it will maintain its action on the body. Nevertheless, the gyroscopic momentum is quantified through multiple methods of classical mechanics by
is constant in time, it will maintain its action on the body. Nevertheless, the gyroscopic momentum is quantified through multiple methods of classical mechanics by
 (3)
(3)
If we consider the disk with its own angular velocity  and subject it to a new noncoaxial torque
and subject it to a new noncoaxial torque , we find that it initiates a new angular velocity
, we find that it initiates a new angular velocity  about an axis perpendicular to the new torque
about an axis perpendicular to the new torque  and not about its own axis. Therefore, we infer that the field of inertial forces generated in the rotating frame by the new noncoaxial torque
and not about its own axis. Therefore, we infer that the field of inertial forces generated in the rotating frame by the new noncoaxial torque  and acting upon a moving body with angular velocity
and acting upon a moving body with angular velocity  and inertial momentum I about that axis of rotation (and thus with angular momentum
and inertial momentum I about that axis of rotation (and thus with angular momentum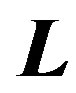 ) will force the moving body to attain orbital motion at the angular velocity
) will force the moving body to attain orbital motion at the angular velocity  defined by the scalar quotient
defined by the scalar quotient
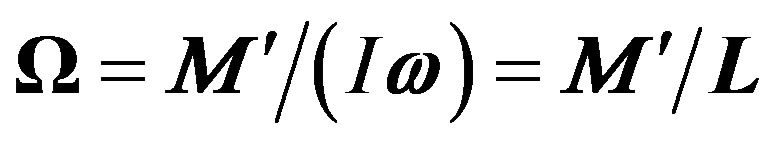 (4)
(4)
The angular velocity  can be observed at the same time as the initial angular velocity,
can be observed at the same time as the initial angular velocity,  which remains constant within the body. Therefore, instead of the discriminating Poinsot hypothesis [13-15], which supposes that angular momentums are coupled to each other and distinct from linear nonstatic momentums, I propose, for translational motion, the hypothesis that the translational velocity field couples to the anisotropic velocity field that is generated by the second noncoaxial torque, forcing the center of mass of the disk to modify its path with no external force applied. Therefore, we obtain an orbital motion
which remains constant within the body. Therefore, instead of the discriminating Poinsot hypothesis [13-15], which supposes that angular momentums are coupled to each other and distinct from linear nonstatic momentums, I propose, for translational motion, the hypothesis that the translational velocity field couples to the anisotropic velocity field that is generated by the second noncoaxial torque, forcing the center of mass of the disk to modify its path with no external force applied. Therefore, we obtain an orbital motion  simultaneously with the constant intrinsic angular velocity
simultaneously with the constant intrinsic angular velocity  of the body. This new orbital motion is generated by a noncoaxial torque and is defined by the rotation of the velocity vector, constant in module.
of the body. This new orbital motion is generated by a noncoaxial torque and is defined by the rotation of the velocity vector, constant in module.
The new external torque , which is supposed to act along the X-axis (Figure 4), will generate a rotation about the Z-axis so that if the initial translational vector
, which is supposed to act along the X-axis (Figure 4), will generate a rotation about the Z-axis so that if the initial translational vector 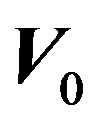 were located on the XY plane, the resulting velocity
were located on the XY plane, the resulting velocity 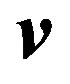 will remain on that plane after the rotation. This rotation may be described by the spatial rotation matrix
will remain on that plane after the rotation. This rotation may be described by the spatial rotation matrix :
:
 (5)
(5)
and will, under my assumption, generate a rotation of the translational vector  in the XY plane.
in the XY plane.
Given that no external force acts on the solid to modify its translational motion, its kinetic linear momentum must remain constant and therefore its translational velocity must remain constant. However, if we accept that the homogeneous translational velocity field couples with the tangential velocity field through the torque ,
,
we can determine the body’s new dynamic state. Under this hypothesis, the motion equation would be determined by the translational velocity of the body’s center of mass, which has not varied in magnitude and therefore will be equal to the initial translational velocity of the body subjected to the spatial rotation mentioned above:
 (6)
(6)
The nondiscriminating coupling proposed in my hypothesis is hence identified as a spatial rotation of velocity:
 (7)
(7)
Thus, the equation of motion can be written as
 (8)
(8)
In a single rotation, the rotational operator  transforms the initial velocity
transforms the initial velocity  into the velocity
into the velocity , both situated in the same plane. We find that the rotational operator
, both situated in the same plane. We find that the rotational operator  is a function of sine or cosine of
is a function of sine or cosine of , which clearly indicates the relation between the angular velocity
, which clearly indicates the relation between the angular velocity  of the orbit and the torque
of the orbit and the torque  and the initial angular velocity
and the initial angular velocity . Thus, I have derived a simple mathematical relation between the angular velocity
. Thus, I have derived a simple mathematical relation between the angular velocity  of the body and its translational velocity
of the body and its translational velocity .
.
Equation (6) is a general equation of motion for bodies with angular momentum that are subjected to successive noncoaxial torques. For this equation, the rotational operator 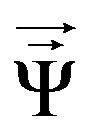 serves as a matrix that transforms the initial velocity, by means of rotation, into the velocity that corresponds to each successive dynamic state.
serves as a matrix that transforms the initial velocity, by means of rotation, into the velocity that corresponds to each successive dynamic state.
In short, this simplified mathematical model implies that it would be possible that moving bodies subjected to successive noncoaxial torques would initiate orbital motion as a result of inertial dynamic interactions such that, while maintaining constant initial angular momentum and the second torque, its center of mass would follow a closed orbit without requiring any centripetal force (Figure 5).
Thus, we can associate dynamic effects to velocity and we find a clear mathematical correlation between rotation and translation. This mathematical connection allows us to identify a physical relation between transfers of rotational kinetic energy to translational kinetic energy and vice versa.
A different approach is thus necessary to analyze the dynamics of bodies undergoing acceleration by rotation. In these cases, we cannot apply the same axioms and

Figure 5. (Color online) Computer-simulated path of the center of mass of a moving object, which has intrinsic rotation and is simultaneously subjected to an external torque noncoaxial with its intrinsic angular momentum when both, the applied moment and translational velocity of the moving object are constant. For this simulation, the tangential velocity was 5 m/s.
premises as used for inertial systems. In accordance with the proposed dynamic hypotheses, I simulated the threedimensional motion of an object in such a situation (i.e., with intrinsic angular momentum and simultaneously subjecting to an external noncoaxial torque) and obtained open or closed trajectories. The deduced equation of motion (Equation (6)) correctly predicts the path observed in my experimental model system (Figure 5).
6. Conclusions
The present text and the accompanying video Theory of Dynamic Interactions provide only a brief summary of the studies carried out over the last twenty years to propose a Rotational Dynamics of Interactions applicable to bodies subjected to multiple successive noncoaxial torques. The initial hypotheses are based on new criteria involving velocity coupling and have been confirmed by experiments and mathematical modeling that allows accurate physical simulations. In this study, I found a clear correlation between the initial speculations, original hypotheses, mathematical simulation, deduced physical laws, experiments, and mathematical models corresponding to the equations of motion that result from the proposed dynamics laws.
As a result of this dynamic investigation work we can propose the following conclusions:
1) There is a wide subject area not yet developed in rotational dynamics inasmuch as rigid bodies are subjected to accelerations caused by simultaneous non coaxial rotations.
2) This area of knowledge can be analyzed under relativistic and non relativistic mechanics. Hypotheses are based on new criteria about speed coupling and rotational inertia.
3) In the exposed experimental non relativistic tests carried out, we have concluded that new general laws of behavior can be obtained, based in the analysis of the dynamics fields created.
4) We have obtained an equation of motion for rigid bodies in translational motion with intrinsic angular momentum, when subjected to non-coaxial pairs, which defines the dynamic behavior of rigid bodies in these cases.
5) We find a clear mathematical correlation between rotation and translation. This mathematical connection allows us to identify a physical relation between transfers of rotational kinetic energy to translational kinetic energy and vice versa.
6) The mathematical model implies that it would be possible that moving bodies subjected to successive noncoaxial torques would initiate orbital motion as a result of inertial dynamic interactions.
7) While maintaining constant initial angular momentum and the second torque constant, the center of mass of the moving bodies would follow a closed orbit without requiring any centripetal force.
8) The theory also allows to give an answer to an initial aporia: to be aware and to understand the physical and mathematical correlation between orbitation and intrinsic rotation.
An example of the theory is the feared roll coupling of the aeroplanes. It happens when a plane, which is flying a screw or any other kind of air acrobatics which implies, for example, a turn around its main inertia axe, starts a new steering manoeuvre with curved trajectory. According to the supported dynamic hypotheses, the non-homogeneous distribution of speeds, generated by the new non-coaxial rotation of the plane mass, couples to the field of translation speed, causing an unintentional deviation of the trajectory, as well as a possible loss of the plane control.
I developed this dynamic model and its background in two books about non-Newtonian mechanics: The Flight of the Boomerang [3], an essay in honor of the physicist Miguel Catalán, and A Rotating World [6].
The result of this project is the demonstration of a rational field theory that gives a new understanding of the behavior of matter. In my opinion, the application of these dynamic hypotheses to astrophysics, astronautics, and other fields of physics and technology will allow new, surprising, and stimulating advances.
The result of this project is the conception of an innovative dynamic theory, which specifically applies to rigid rotating physical systems and which has numerous and significant scientific and technological applications, especially in orbital dynamics, orbit determination, and orbit control. For instance:
• Variation of the affecting torque, arises when subjecting intrinsic angular momentum bodies to new non-coaxial momentums.
• To conceive an intrinsic rotating mobile solid, which could be exclusively controlled due to Dynamic Interactions.
• To calculate the trajectory of any intrinsic angular momentum solid in space.
• To propose a new steering system independent from a rudder or any other external element.
We can suggest advances in the studies and application related to orbital mechanics, guidance, navigation, and control of single or multi-spacecraft systems as well as space robotics and rockets [16].
For those who are interested in cooperating with this independent research project may request for additional information by writing me at gestor@advanceddynamics.net or visiting www.advanceddynamics.net.