Stability Criteria of Solutions for Stochastic Set Differential Equations ()
1. Introduction
Recently, the field of stochastic differential equations (SDEs) has been studying in a very abstract method. Instead of considering the behaviours of one solution of (SDEs), one studies its set-valued solution. Instead of studying a (SDEs), some study stochastic differential inclusion (SDIs) (see e.g. [2-4] and references therein), stochastic fuzzy differential equations (SFDEs), (see e.g. [5-6] and references therein) stochastic set differential equations (SSDEs) (see e.g. [7-10] and references therein), stochastic set differential equations with selector (see [11-13]). Latest, the existence and uniqueness of solutions to the stochastic set differential equations were studied in [1]. We remark that the problems of properties of stochastic set solution are still open.
We organize this paper as follows: In Section 2, we recall some basic concepts and notations which are useful in next sections. In Section 3, we study some kinds of stability properties such as stable, asymptotically stable, exponentially stable by Lyapunov and some other stability criterion. In Section 4, we give the examples and further research of this paper.
2. Preliminaries
We recall some notations and concepts presented in detail in recent series works of V. Lakshmikantham et al (see [14]). Let 
denote the collection of all nonempty compact convex subsets of
. Given
, the Hausdorff distance between A and B is defined by
(2.1)
and
—the zero points set in
. It is known that 
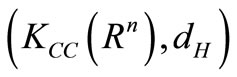is a complete metric space and
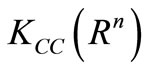is a complete and separable with respect to
. We define the magnitude of a nonempty subset 
as,
The Hausdorff metric (2.1) satisfes the properties below:
1) 
2) 
3) 
4) 
for all 
and
.
If 
and
, then
Given a complete probability space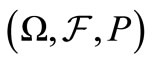 
with a filtration
satisfying the usual conditions. Let
be an
—adapted one dimensional Wiener process defined on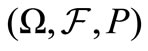 
and
, with 
is one-dimensional “white noise”, i.e., the time derivative of the Wiener process. In [1], authors considered the initial valued problem (IVP) for a set stochastic differential equation (SSDE) as follows
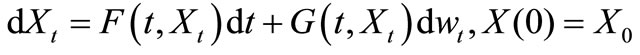(2.2)
where
,
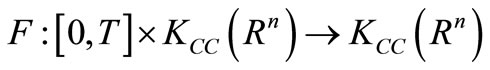
is measurable multifunction and Aumann integrably bounded.
is measurable multifunction and 
integrably bounded, 
is an 
-measurable multifunction.
Definition 2.1. (see [1]) Let a set-valued stochastic process 
satisfy:
1) 
for every 
;
2) 
is continuous mapping with respect to the metric
;
3) for every
:
where 
is an
—measurable multifunction. Then 
is solution of (2.2).
Definition 2.2. Let set-valued stochastic processes
, we have the following definitions:
1) For every
,
2) For every
,
Using the properties of the Hausdorff distance one can formulate the following results
Lemma 2.1.
1) if
then 
2) if
then 
3) If 
and 
reconstants, then 
Corollary 2.1. (see [7]) Let set-valued stochastic processes 
we have the following confirms:
1)
;
2)
;
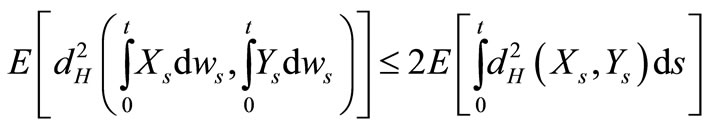3)
;
4)
.
Definition 2.3. A solution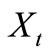 
to Equation (2.2) is unique if for every
:
where 
is any solution to Equation (2.2).
Assume that 
satisfy the following hypotheses:
(H1) For every set 
the mappings
: 
are nonanticipating multifunctions.
(H2) There exists a constant
, such that
(H3) There exists a constant
, such that
(H4) There exists a function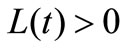
, such that
where
.
(H5) There exists a function
, such that
where
.
Corollary 2.2. (see [1], Theorem 7) Assume 
be an
—measurable multifunction and F, G satisfy (H1)-(H3), then SSDE (2.2) has a unique solution and satisfies estimate
Corollary 2.3. Assume 
be an
—measurable multifunction and F, G satisfy (H1), (H4)-(H5), then SSDE (2.2) has a unique solution and satisfies estimate
3. Main Results
In this section, we study some kinds of stability properties such as stable, asymptotically stable, exponentially stable by Lyapunov and some other stability criteria such as equi, uniform and equi-asymptotical stabilities for SSDE.
Definition 3.1. The trivial stochastic set solution of SSDE Equation (2.2) is said to be
(LS) Lyapunov stable, if for each 
and 
there exist a
, such that 
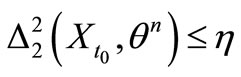
implies
.
(ALS) Asymptotical Lyapunov stable, if it is (LS) and
.
(ELS) Exponent Lyapunov stable, if there exist 
, such that:
Definition 3.2. The trivial stochastic set solution of SSDE Equation (2.2) is said to be:
(S1) Equi-stable, if for each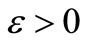
, and 
there exists 
such that 
implies that
,
;
(S2) Uniformly stable, if 
in (S1) is independent of
;
(S3) Quasi-equi-asymptotically stable, if for each
, there exists 
and 
such that 
implies
, for all
;
(S4) Quasi-uniformly-asymptotically stable, if 
and 
in (S3) are independent of
;
(S5) Equi-asymptotically stable, if (S1) and (S3) hold simultaneously;
(S6) Uniformly asymptotically stable, if (S2) and (S4) hold simultaneously;
(S7) Exponent-asymptotically stable, if exist 
such that 
for all 
Lemma 3.1. According to the Definitions 3.1 and Definition 3.2, we can say that 1) The stochastic set solution of SSDE E (2.2) is (S1) if and only if it is (LS) that means (S1) 
(LS).
2) (S6) 
(ALS).
3) (S7) 
(ELS).
4) (S6) or (ALS) 
(S6).
5) (S6) 
(S4).
Thus we have to prove (S1), (S6) and (S7).
Next, we present some results about (S1)-(S6) of solution with using the Lyapunov-like functions.
Theorem 3.1. Suppose that the positive Lyapunov-like function
satisfies the following conditions:
1)
where 
is Lipschitz constant, for all
,
,
;
2) The Dini derivative
where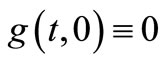
,
;
If 
is any solution of SSDE Equation
(2.2) Such that
, then we have
where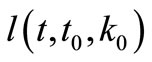 
is a maximal solution of ordinary differential equation (ODE)
(3.1)
Proof. Let 
be any solution of SSDE Equation (2.2) existing on
. We define the function 
so that
.
Now for small
, by our assumption it follows that
by using the Lipschitz condition give (1). Thus
Since
and 
is any solution of SSDE Equation (2.1), we find that
We therefore have the scalar differential inequality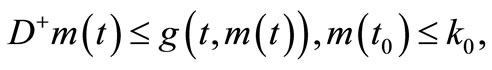 
which yields, as before, the estimate 
where 
is a maximal solution of ODE (3.1). This proof is complete.
Corollary 3.1. If the Lyapunov-like function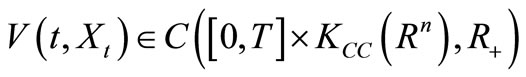 
satisfies conditions in Theorem 3.1 then we have the estimate:
Next, putting
Theorem 3.2. Assume that for SSDE Equation (2.2) exists the Lyapunov like function 
which satisfies the conditions of Theorem 3.1.
a) If there exist the positive functions 
are strictly increasing such that:
1) 
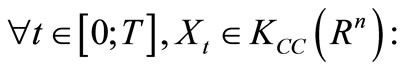
and
, then (S1) holds.
Futhermore, there exists 
such that
2) If
, then (S3) holds.
3) If
, then (S5) holds.
b) If there exist the positive functions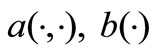 
are strictly increasing and 
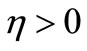such that:
1) 
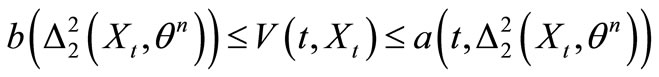
and
, then (S2) holds.
Futhermore, there exists 
such that.
2) If
, then (S4) holds.
3) If 
then (S6) holds.
Proof. Let 
and 
be given, choosing 
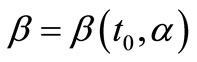such that 
with this we have (S1).
If this is not true, there would exists a stochastic set solution 
of SSDE Equation (2.2) and 
such that
with
. By using Corollary 3.1 and a/1, we have
and condition
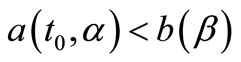as result, yield:
This contradiction proves that (S1) holds.
Next, we have to prove that: 
there exists a 
and number 
such that:
implies
for
. Let 
and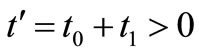
.
Choosing 
such that 
with this we have (S3). If this is not true, there would exists a stochastic set solution 
of SSDE Equation
(2.2) such that, 
and
where
, for 
By using assumption (a/2) of this theorem shows that
, 
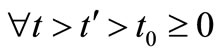and yields:
This contradiction proves that (S3) holds.
The affirmation for (S5) is proved analogous to the proof of the affirmations for (S1), (S3).
Next, we have to prove that (S2) holds:
By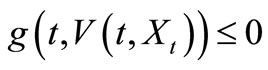 
implies 
and
,
.
Thus for all 
and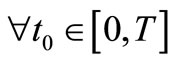 
the affirmation for (S1) holds, that means the affirmation for (S2) holds.
Next, we have to prove that (S4) holds. According to assumption b) of Theorem 3.2
1) 
2) 
For all
, we have
As a result,
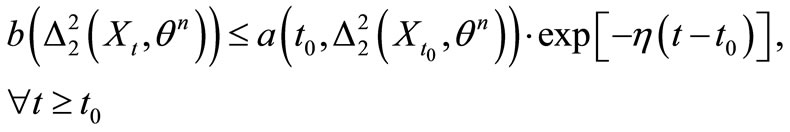
and (S4) holds.
The affirmation for (S6) is proved analogous to the proof of the affirmations for (S2), (S4).
Corollary 3.2. Assume that for SSDE Equation (2.2) exists the Lyapunov like function 
which satisfies the conditions of Theorem 3.1, and exist the positive numbers 
such that 
.
If
, then (S7) holds.
Proof. The proof for (S7) is proved analogous to the proof of the affirmations for (S4).
4. Some Applications of Stochastic Set Differential Equations
For example, in a finance market we consider some stock price at time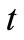 
denoted by 
which is a random variable defined on the probability space
. Owing to the quick fluctuation of the stock price from time to time or to the existence of missing data, we may not precisely know the price
. A possible model for this situation would be to give the upper and the lower prices (i.e. a margin for the error in the observation). Then we obtain an nterval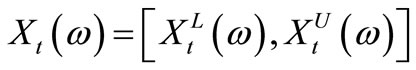
, which is a special kind of a set-valued random variable, ontains not only randomness but also impreciseness, and we assume 
is certainly in this interval.
For example different, in environmental of the insurance premium, the risks is considered a main material of this industry. Beside that, the risks are random factors and associating with premiums, so insurance premiums should be built on the basis of risks to price insurance which could compensate and balance the damage occurs to their business costs. Otherwise, the risks are some kinds different and levels of influence are different, so they could influence to levels of price of the insurance premium.
Hence, we may not precisely know the price of the insurance premium such that be beneficial to company of the insurance and customers. Then, in special the case we assume 
is certainly in this interval which admissible prices.
Example 4.1. (Stock prices) Let 
denote the price of a stock at time
, where 
(i.e. interval-valued). We can model the evolution of 
and the relative change of price, evolves according to the SSDE under the form
(4.1)
for all
, for certain constants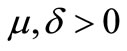
, called the drift and the volatility of the stock.
Since coefficients in Equation (4.1) satisfy the conditions in Corollary 2.2, there is a unique solution of Equation (4.1). This means that for 
SSDE (4.1) satisfies the following interval-valued stochastic differential equation
(4.2)
for all
. That is,
Since
, 
and 
are the solutions of the following stochastic differential system
(4.3)
(4.4)
We can slove Equation (4.3) and Equation (4.4) by classic methods. Thus, the solutions of Equation (4.3) and Equation (4.4) respecttively are
and
.
Its graphical representation can be seen in Figure 1.
From here it is easily verifiable stability criteria of solution to Equation (4.1).
5. Further Research
In the future, we will concentrate all our efforts on other properties of this kind of equation discussed in our paper, such as on the existence of extremal solutions for SSDEs (2.2). Beside that, set-valued stochastic differential equations and their solutions seem to be a starting point for
Figure 1. Solution of Example 4.1 in case μ = 2, δ = 1.
further development in the theory of control for SSDEs. Below we present the main idea, we consider the setvalued stochastic control differential equations (SSCDEs) under the form
(4.5)
where 
are continuous multifunctions, state set 
and 
is different controls, inclusion: admissible control, feedback control and contraction control. The problems of the existence and properties of solutions to SSCDEs Equation (4.5) is still open.
6. Acknowledgements
The authors gratefully acknowledge the referees for their careful reading and many valuable remarks which improved the presentation of the paper. The authors thank the partial financial support of AM editorial office.