The Study and Investigation of Electron Trajectories in Free Electron Laser with Realizable Helical Wiggler and Ion Channel Guiding: A Computational Study ()
1. Introduction
In this paper, a detailed analysis of electron trajectories in a realizable helical wiggler in the free electron laser with ion-channel guiding is presented. We investigate the conditions for the stability of electron trajectories; and the calculations are illustrated. We indicate that there are differences between stable and unstable conditions for electron trajectories, and between the ideal 2D helical wiggler and 3D realizable helical wiggler. The ion channel with positive ions is analyzed as a guiding tool in order to improve the performance of free electron lasers with ideal helical wiggler [1-5] and ideal planar wiggler [6,7], the electron trajectories in ideal planar wiggler are computed [6,7]. When the electron beam transits this channel, the existence of positive ions create electrostatic field in the latitudinal direction, and cause the electron beam to focus in the direction of laser cylinder’s axis (active medium).
In this paper, the electron trajectories in the free electron laser with realizable helical wiggler and ion channel are investigated. The latitudinal electrostatic field due to positive ions with uniform density and static magnetic wiggler are considered. The relativistic electron-motion equation is solved. Finally, through employing the multinomial equations in the steady state, the stable and unstable electron trajectories including two orbital groups are obtained [8].
2. Results and Discussion
2.1. The Electron Trajectories
In this paper, for the first time, we proposed a novel analytical and numerical approach toward studying electron trajectories in free electron laser with realizable helical wiggler and ion channel guiding. In the free electron laser with the ideal helical magnetic wiggler, the magnetic wiggler has only two components in the directions of x and y, and the component z is neglected [8]. However, in the realizable wiggler, all the components are input to approach the laser’s real form.
The realizable helical magnetic wiggler in the cylindrical coordinates is defined as follows [8-23]:
 (1)
(1)
where BW is the wiggler amplitude,  is the Bessel function,
is the Bessel function, 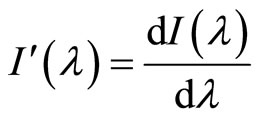 ,
,  ,
,  is the wiggler wave number, and
is the wiggler wave number, and .
.
The electrostatic field resulting from the ion channel can be written as [6,7]:
 (2)
(2)
where 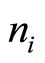 is the positive ions’ density, and e is the absolute value of electrons’ charge. In the presence of these fields, the motion equation is as follows [8]:
is the positive ions’ density, and e is the absolute value of electrons’ charge. In the presence of these fields, the motion equation is as follows [8]:
 (3)
(3)
where  is the electron vector velocity, and c is the light velocity. Solving the motion equations in order to investigate electron trajectories in the Cartesian coordinates is difficult; accordingly, we employ the wiggler coordinates [9-23]. The realizable helical magnetic wiggler in this coordinate system is as the following form [8]:
is the electron vector velocity, and c is the light velocity. Solving the motion equations in order to investigate electron trajectories in the Cartesian coordinates is difficult; accordingly, we employ the wiggler coordinates [9-23]. The realizable helical magnetic wiggler in this coordinate system is as the following form [8]:
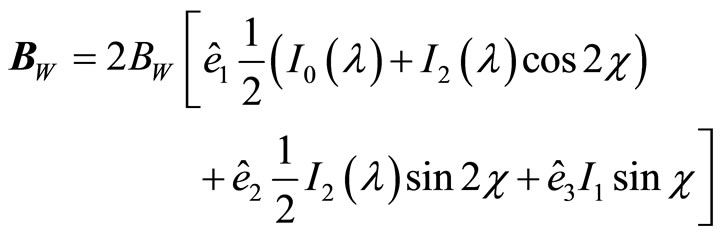 (4)
(4)
Through inserting Equations (2) and (4) into Equation (3), the motion equation’s components are as follows:
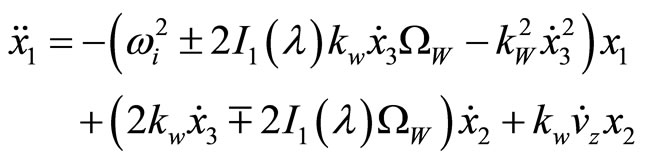 (5)
(5)
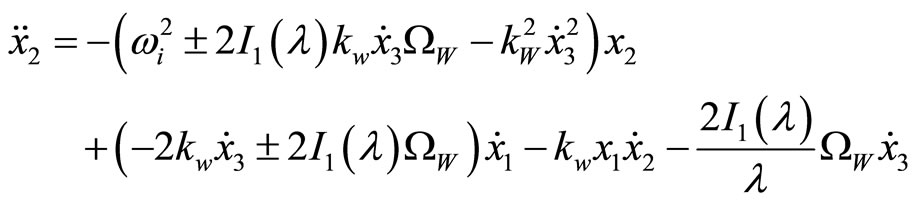 (6)
(6)
 (7)
(7)
 (8)
(8)
 (9)
(9)
where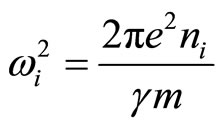 ,
,  ,
,  is the relativistic factor, m is the static electron’s mass. The solutions to Equations (5)-(9) in the steady state are as the forms below:
is the relativistic factor, m is the static electron’s mass. The solutions to Equations (5)-(9) in the steady state are as the forms below:
 (10)
(10)
 (11)
(11)
 (12)
(12)
 (13)
(13)
 (14)
(14)
If 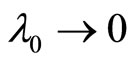 or
or  (latitudinal velocity) inclines toward zero, the steady-state results are fulfilled [1-5].
(latitudinal velocity) inclines toward zero, the steady-state results are fulfilled [1-5].
In regard to Equation (10), when the below condition exists:
 (15)
(15)
The latitudinal velocity ( ) dramatically increases. In other words, there is a resonance creating two orbital groups as the following forms:
) dramatically increases. In other words, there is a resonance creating two orbital groups as the following forms:
The orbital group I: 
The orbital group II: 
2.2. The Stability of Trajectories
The stability of steady trajectories is achieved through inputting perturbations of ,
, 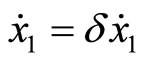 ,
,  ,
,  ,
,  ,
,  and
and  around the steady state (
around the steady state ( and
and  are constant) to Equations (5)-(8):
are constant) to Equations (5)-(8):
 (16)
(16)
 (17)
(17)
 (18)
(18)
Through the derivation of Equations (16) and (17) with respect to time, and the replacement of Equation (18), the two equations are coupled together:
 (19)
(19)
 (20)
(20)
 (21)
(21)
 (22)
(22)
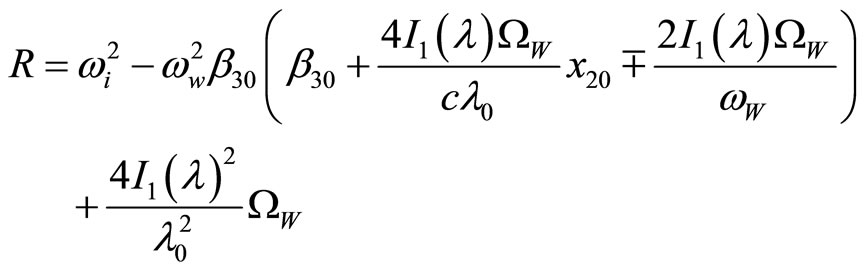 (23)
(23)
 (24)
(24)
 (25)
(25)
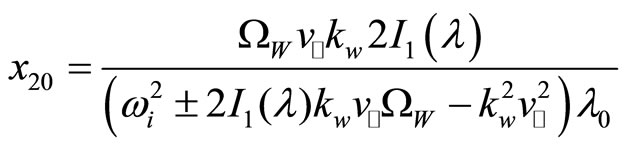 (26)
(26)
where  and
and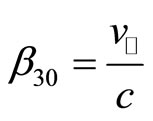 . Considering the oscillating commutation:
. Considering the oscillating commutation:
 (27)
(27)
where  is the commutation amplitude, and
is the commutation amplitude, and  is its frequency. Finally, Equations (19) and (20) are transformed into the forms below:
is its frequency. Finally, Equations (19) and (20) are transformed into the forms below:
 (28)
(28)
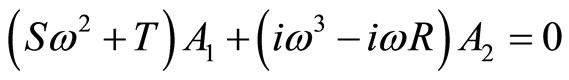 (29)
(29)
The above equation is a second-order equation according to , and the stability condition is as the following form:
, and the stability condition is as the following form:
 (30)
(30)
With reference to this condition (Equation (30)), Equation (27) is oscillating.
The graph of electron’s axial velocity (βII) by  for ideal wiggler is illustrated in Figure 1 [6,7]; Figure 2 indicates
for ideal wiggler is illustrated in Figure 1 [6,7]; Figure 2 indicates  by
by 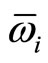 for realizable wiggler (in both figures, we consider
for realizable wiggler (in both figures, we consider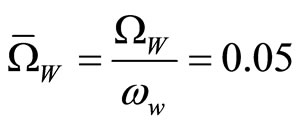 ). In contrast with the ideal wiggler, there is instability in the orbital group II. Furthermore, the declined resonance state decreases the performance. It is anticipated that as the performance slumps on account of unstable trajectories in the realizable wiggler, the difference between theoretical and empirical results of ideal wiggler reduces [8].
). In contrast with the ideal wiggler, there is instability in the orbital group II. Furthermore, the declined resonance state decreases the performance. It is anticipated that as the performance slumps on account of unstable trajectories in the realizable wiggler, the difference between theoretical and empirical results of ideal wiggler reduces [8].
3. Conclusion
In this paper, the steady electron trajectories in the free electron laser with the realizable helical magnetic wiggler and ion channel guiding are investigated using the
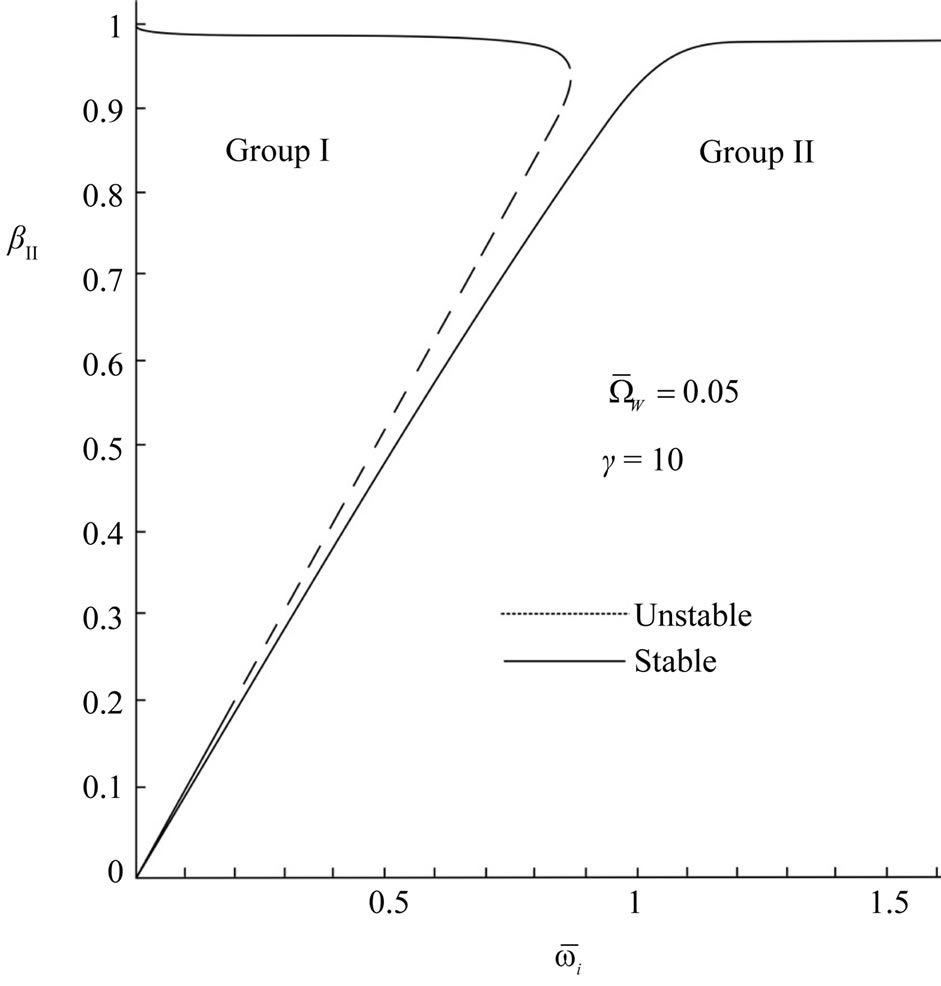
Figure 1. The diagram of βII by  for the ideal wiggler.
for the ideal wiggler.

Figure 2. The diagram of βII by  for the realizable wiggler.
for the realizable wiggler.
relativistic motion equation, and compared with the ideal state. In contrast with the ideal wiggler, in the realizable helical wiggler, the orbital group II has unstable trajectories. The unstable trajectories increase in proportion to the ideal wiggler, and the resonance region reduces. Therefore, it is expected that the difference between theoretical and empirical results of laser performance, observed in the ideal state, also decreases.
4. Acknowledgements
The work described in this paper was fully supported by grants from the Institute for Advanced Studies of Iran. The authors would like to express genuinely and sincerely thanks and appreciated and their gratitude to Institute for Advanced Studies of Iran.
NOTES