1. Introduction
We begin with simple, finite, connected and undirected graph  with
with vertices and
vertices and  edges. For standard terminology and notations we follow Gross and Yellen [1]. We will provide brief summary of definitions and other information which are necessary for the present investigations.
edges. For standard terminology and notations we follow Gross and Yellen [1]. We will provide brief summary of definitions and other information which are necessary for the present investigations.
Definition 1.1 If the vertices are assigned values subject to certain condition(s) then it is known as graph labeling.
Any graph labeling will have the following three common characteristics:
1) A set of numbers from which vertex labels are chosen;
2) A rule that assigns a value to each edge;
3) A condition that this value has to satisfy.
According to Beineke and Hegde [2] graph labeling serves as a frontier between number theory and structure of graphs. For a dynamic survey of various graph labeling problems along with extensive bibliography we refer to Gallian [3].
Definition 1.2 A mapping  is called binary vertex labeling of
is called binary vertex labeling of  and
and  is called the label of the vertex
is called the label of the vertex  of
of  under
under .
.
Notation 1.3 If for an edge , the induced edge labeling
, the induced edge labeling  is given by
is given by
 . Then
. Then

Definition 1.4 A binary vertex labeling  of a graph
of a graph 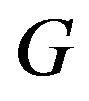 is called a cordial labeling if
is called a cordial labeling if  and
and . A graph
. A graph 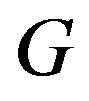 is cordial if it admits cordial labeling.
is cordial if it admits cordial labeling.
The concept of cordial labeling was introduced by Cahit [4]. Some labeling schemes are also introduced with minor variations in cordial theme. Some of them are product cordial labeling, total product cordial labeling and prime cordial labeling. The present work is focused on prime cordial labeling.
Definition 1.5 A prime cordial labeling of a graph  with vertex set
with vertex set  is a bijection
is a bijection  and the induced function
and the induced function  is defined by
is defined by
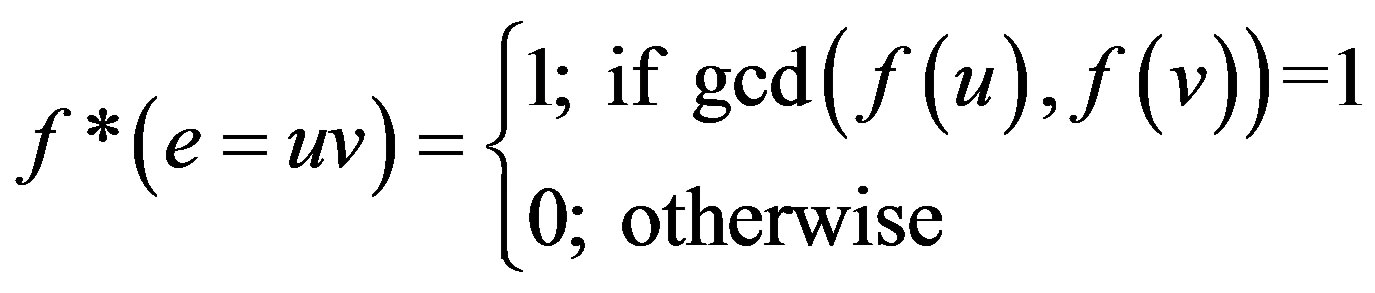
satisfies the condition 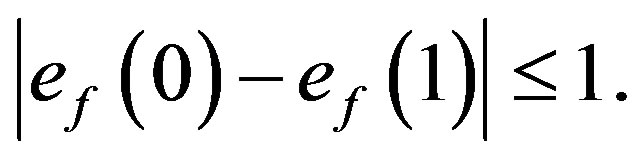 A graph which admits prime cordial labeling is called a prime cordial graph.
A graph which admits prime cordial labeling is called a prime cordial graph.
The concept of prime cordial labeling was introduced by Sundaram [5] et al. and in the same paper they have investigated several results on prime cordial labeling. Vaidya and Vihol [6] have also discussed prime cordial labeling in the context of graph operations while in [7] the same authors have discussed prime cordial labeling for some cycle related graphs. Vaidya and Shah [8] have investigated many results on this concept. In the present paper we obtain some new prime cordial graphs.
Definition 1.6 Bistar is the graph obtained by joining the apex vertices of two copies of star .
.
Definition 1.7 For a graph G the split graph is obtained by adding to each vertex v a new vertex  such that
such that 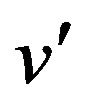 is adjacent to every vertex that is adjacent to v in G. The resultant graph is denoted as
is adjacent to every vertex that is adjacent to v in G. The resultant graph is denoted as .
.
Definition 1.8 For a simple connected graph G the square of graph G is denoted by 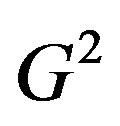 and defined as the graph with the same vertex set as of G and two vertices are adjacent in
and defined as the graph with the same vertex set as of G and two vertices are adjacent in  if they are at a distance 1 or 2 apart in G.
if they are at a distance 1 or 2 apart in G.
Definition 1.9 The middle graph M(G) of a graph G is the graph whose vertex set is  and in which two vertices are adjacent if and only if either they are adjacent edges of G or one is a vertex of G and the other is an edge incident with it.
and in which two vertices are adjacent if and only if either they are adjacent edges of G or one is a vertex of G and the other is an edge incident with it.
2. Main Results
Theorem 2.1  is a prime cordial graph.
is a prime cordial graph.
Proof: Let  be the pendant vertices,
be the pendant vertices,  be the apex vertex of
be the apex vertex of  and
and 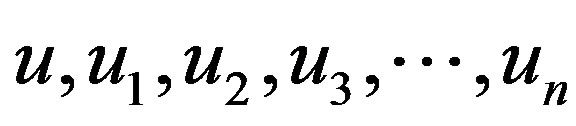 are the vertices corresponding to
are the vertices corresponding to 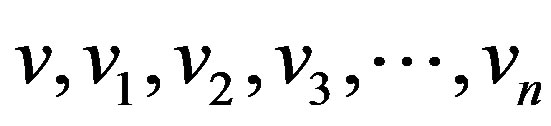 in
in . Denoting
. Denoting  then
then  and
and  .
.
To define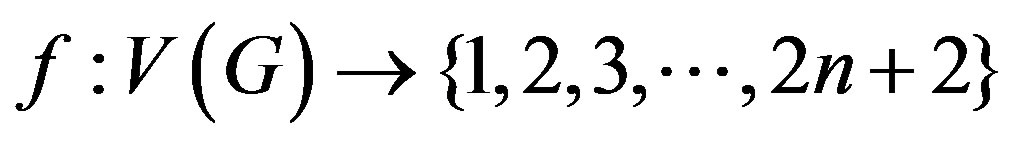 , we consider following two cases.
, we consider following two cases.
Case 1: n = 2, 3 The graphs 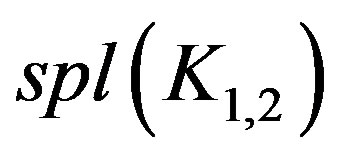 and
and  are to be dealt separately and their prime cordial labeling is shown in Figure 1.
are to be dealt separately and their prime cordial labeling is shown in Figure 1.
Case 2: 

In view of the labeling pattern defined above we have  (for n even) and
(for n even) and
 (for n odd). Thus we have
(for n odd). Thus we have
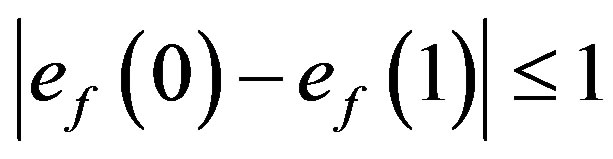 .
.
Hence  is a prime cordial graph.
is a prime cordial graph.
Illustration 2.2 Prime cordial labeling for 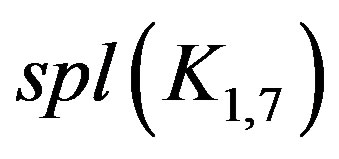 is shown in Figure 2.
is shown in Figure 2.
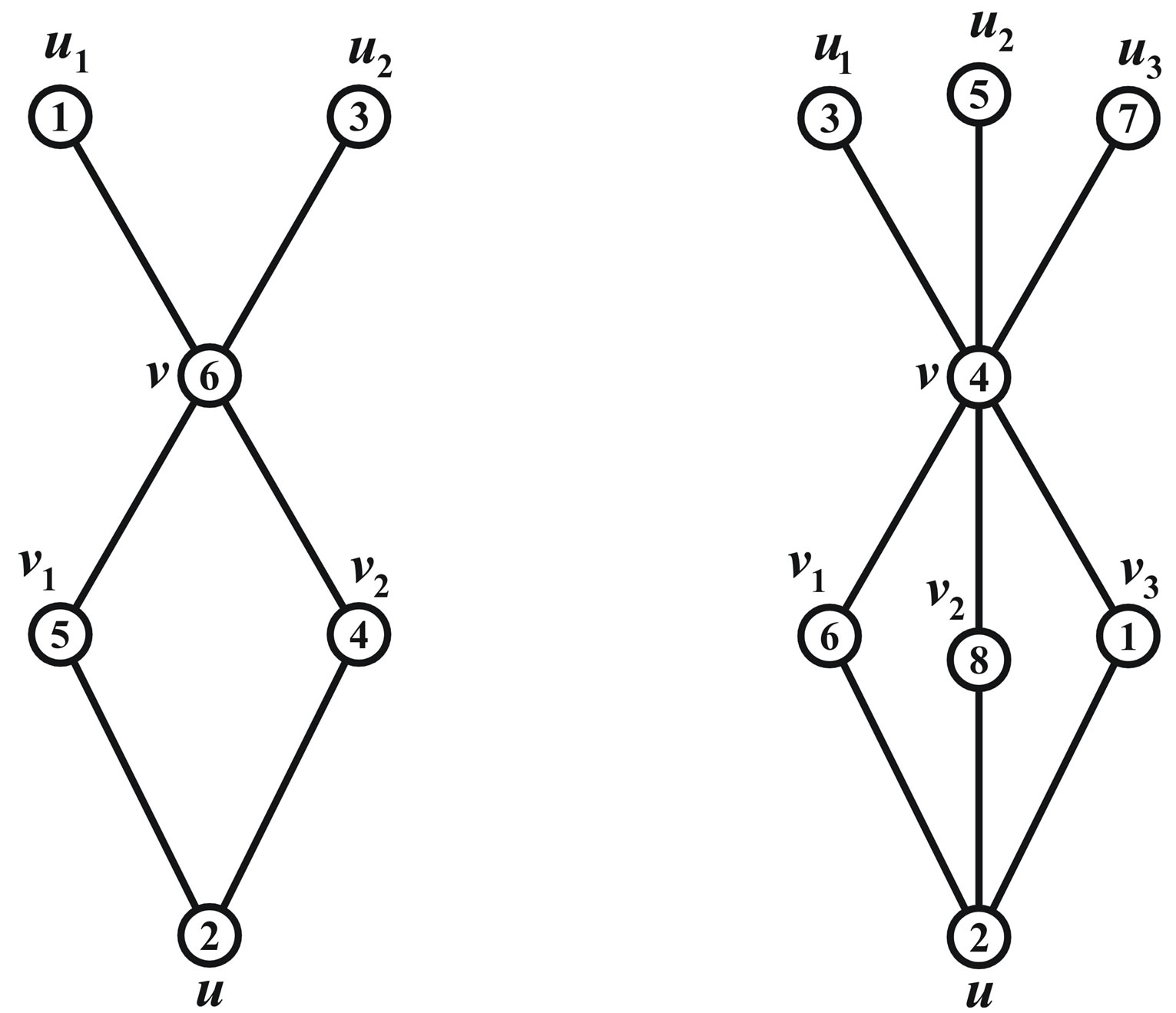
Figure 1. ,
, and their prime cordial labelling.
and their prime cordial labelling.

Figure 2. 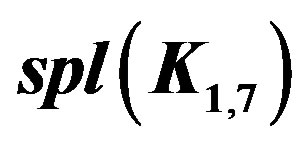 and its prime cordial labelling.
and its prime cordial labelling.
Theorem 2.3  is a prime cordial graph.
is a prime cordial graph.
Proof: Consider  with vertex set
with vertex set
 where
where 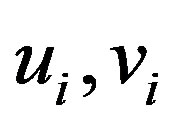 are pendant vertices. In order to obtain
are pendant vertices. In order to obtain  add
add  vertices corresponding to
vertices corresponding to 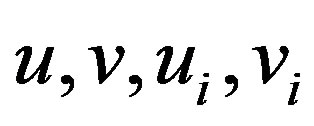 where
where . If
. If  then
then  and
and 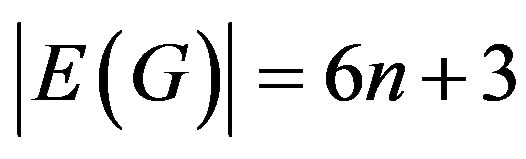 . We define vertex labeling
. We define vertex labeling  as follows.
as follows.

In view of pattern defined above we have  .
.
That is,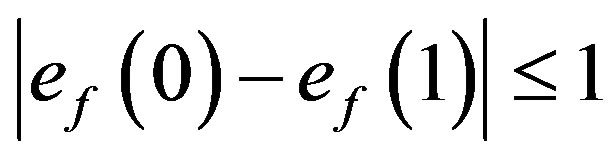 .
.
Hence  is a prime cordial graph.
is a prime cordial graph.
Illustration 2.4 Prime cordial labeling of the graph  is shown in Figure 3.
is shown in Figure 3.
Theorem 2.5  is a prime cordial graph.
is a prime cordial graph.
Proof: Consider  with vertex set
with vertex set  where
where  are pendant vertices. Let G be the graph
are pendant vertices. Let G be the graph  then
then  and
and  .
.
To define , we consider following two cases.
, we consider following two cases.
Case 1: 
The graphs  and
and  are to be dealt separately and their prime cordial labeling is shown in Figure 4.
are to be dealt separately and their prime cordial labeling is shown in Figure 4.
Case 2: 
Choose a prime number p such that ,
,

 , where
, where  is distinct even numbers between 4 and 2n + 2 except 2p with
is distinct even numbers between 4 and 2n + 2 except 2p with .
.
 ,
,
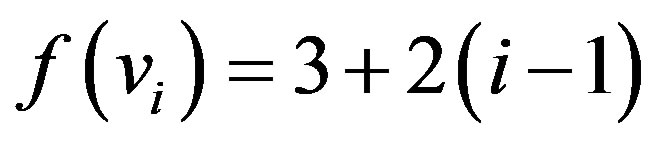 for
for .
.
In view of the above defined labeling pattern we have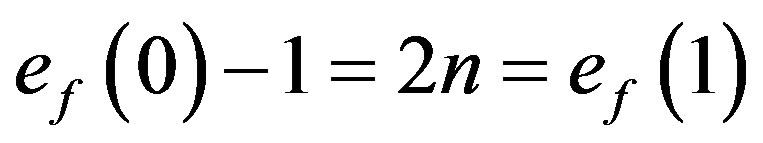 .
.
Thus in both the cases we have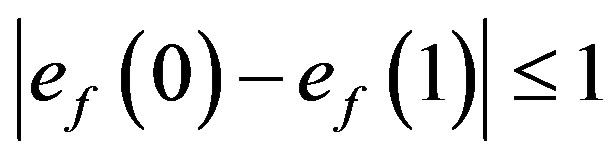 .
.
Hence  is a prime cordial graph.
is a prime cordial graph.
Illustration 2.6 Prime cordial labeling of the graph  is shown in Figure 5.
is shown in Figure 5.

Figure 3.  and its prime cordial labelling.
and its prime cordial labelling.
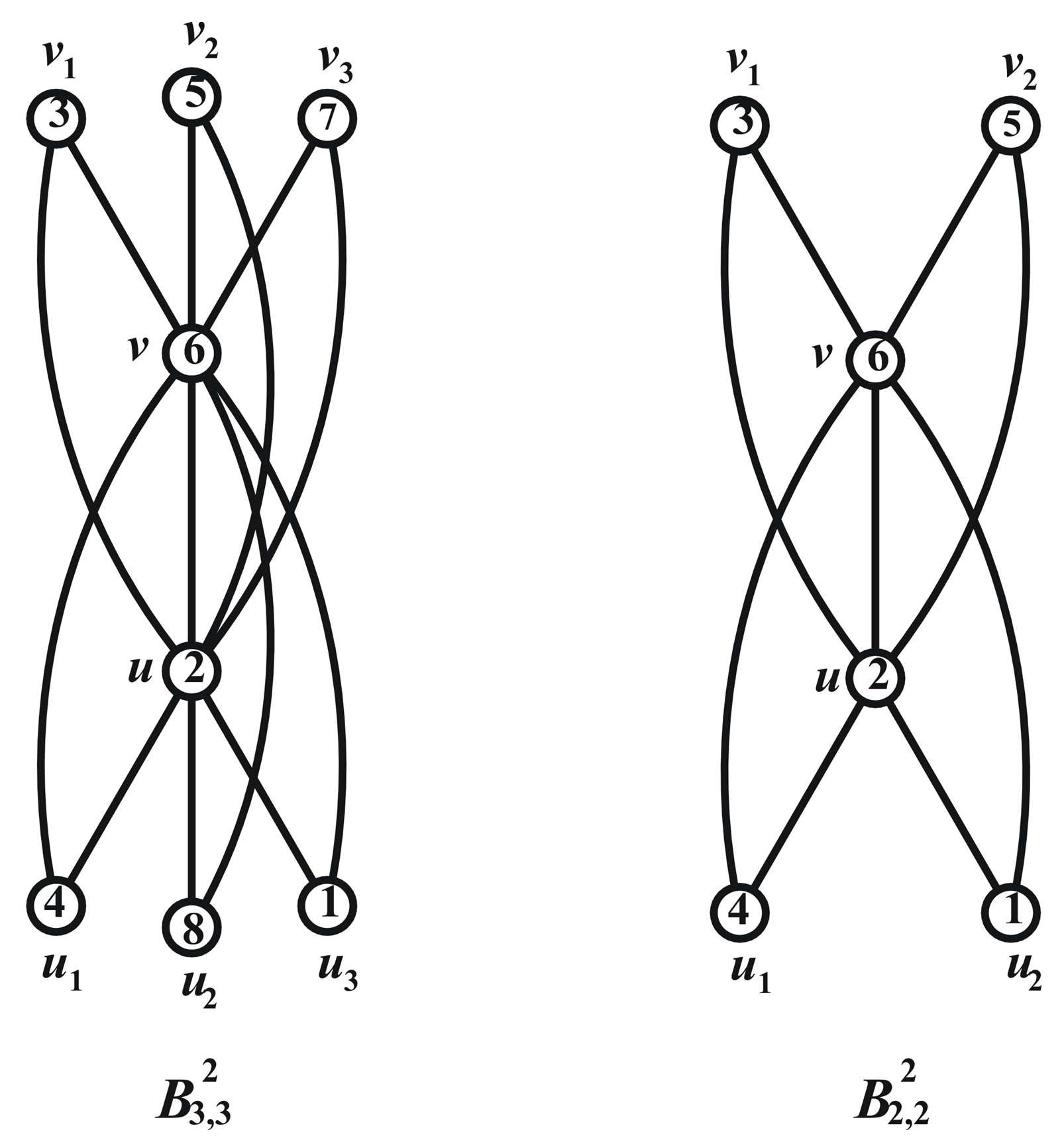
Figure 4. ,
, 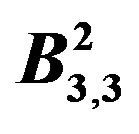 and their prime cordial labelling.
and their prime cordial labelling.
Theorem 2.7 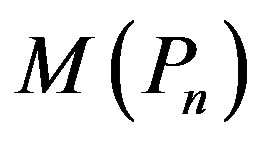 is not a prime cordial graph for
is not a prime cordial graph for 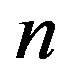 = 2, 3.
= 2, 3.
Proof: Let  and
and  are respectively be the vertices and edges of
are respectively be the vertices and edges of . Add vertices
. Add vertices  corresponding to the edges
corresponding to the edges  in order to obtain middle graph of
in order to obtain middle graph of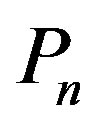 . Let
. Let  be the graph
be the graph . Then
. Then  and
and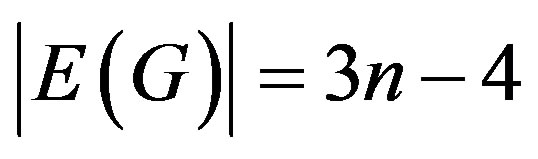 .
.
For the graph  the possible assignment of labels to adjacent vertices are (1,2), (1,3), (2,3). Such assignment will generate no edge with label 0 and two edges with label 1. That is,
the possible assignment of labels to adjacent vertices are (1,2), (1,3), (2,3). Such assignment will generate no edge with label 0 and two edges with label 1. That is, . Therefore
. Therefore  is not a prime cordial graph.
is not a prime cordial graph.
For the graph 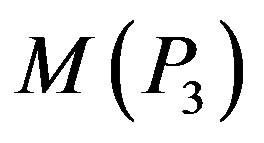 the possible assignment of labels to adjacent vertices are (1,2),(1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4), (3,5). Such assignment will generate maximum one edge with label 0 and minimum four edges with label 1. That is,
the possible assignment of labels to adjacent vertices are (1,2),(1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4), (3,5). Such assignment will generate maximum one edge with label 0 and minimum four edges with label 1. That is, . Therefore
. Therefore  is not a prime cordial graph.
is not a prime cordial graph.
Hence  is not a prime cordial graph for
is not a prime cordial graph for 
Theorem 2.8 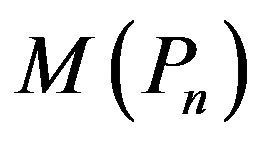 is a prime cordial graph for
is a prime cordial graph for 
Proof: Let 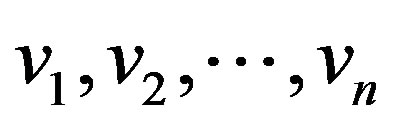 and
and  are respectively be the vertices and edges of
are respectively be the vertices and edges of . Add vertices
. Add vertices  corresponding to the edges
corresponding to the edges  in order to obtain middle graph of
in order to obtain middle graph of . Let
. Let  be the graph
be the graph . Then
. Then  and
and 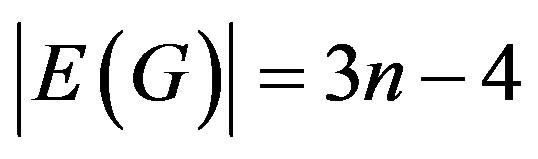 . To define
. To define  , we consider following two cases.
, we consider following two cases.
Case 1:  is even,
is even, 

In view of the above defined labeling pattern we have
 .
.
Case 2:  is odd,
is odd, 

Figure 5. 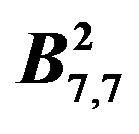 and its prime cordial labelling.
and its prime cordial labelling.
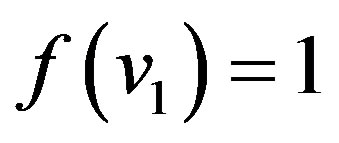 ,
,
 ,
,


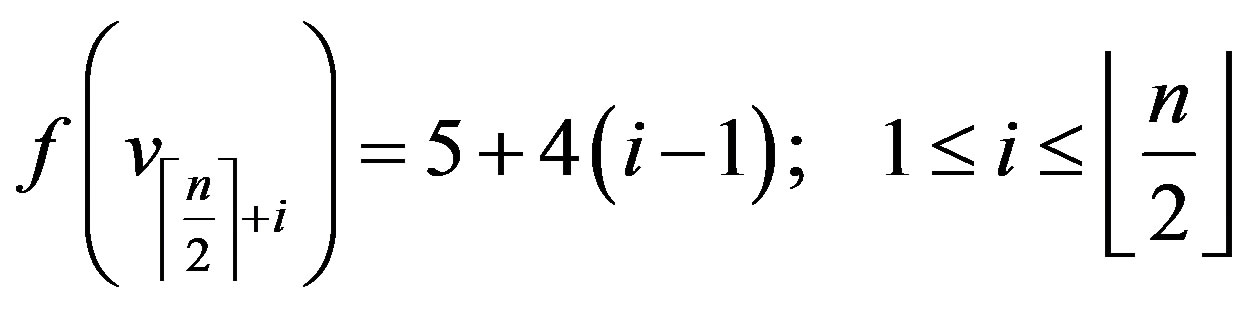


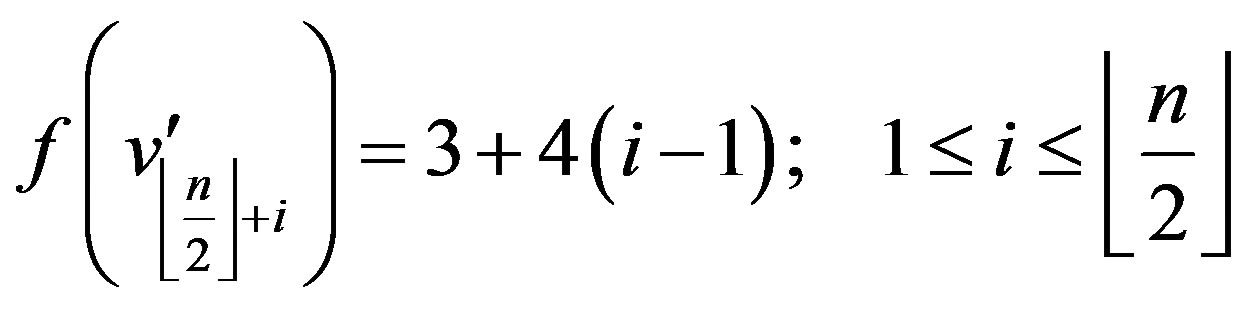
In view of the above defined labeling pattern we have

Thus in both the cases we have .
.
Hence  is a prime cordial graph for
is a prime cordial graph for 
Illustration 2.9 Prime cordial labeling of the graph  is shown in Figure 6.
is shown in Figure 6.
Theorem 2.10  is not a prime cordial graph for n = 3 to n = 7.
is not a prime cordial graph for n = 3 to n = 7.
Proof: Let  be the apex vertex of wheel
be the apex vertex of wheel  and
and  be the rim vertices. Then
be the rim vertices. Then  and
and 
For the graph  the possible pairs of labels of adja-
the possible pairs of labels of adja-

Figure 6.  and its prime cordial labelling.
and its prime cordial labelling.
cent vertices will be (1,2), (1,3), (1,4), (2,3), (2,4), (3,4). Such assignment will generate maximum one edge with label 0 and minimum five edges with label 1. That is, . Hence
. Hence  is not a prime cordial graph.
is not a prime cordial graph.
For the graph  the possible assignment of labels to adjacent vertices will be (1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4), (3,5), (4,5). Such assignment will generate maximum one edge with label 0 and minimum seven edges with label 1. That is,
the possible assignment of labels to adjacent vertices will be (1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5), (3,4), (3,5), (4,5). Such assignment will generate maximum one edge with label 0 and minimum seven edges with label 1. That is, . Hence
. Hence  is not a prime cordial graph.
is not a prime cordial graph.
For the graph  the possible assignment of labels to adjacent vertices will be (1,2), (1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6), (4,5), (4,6), (5,6). Such assignment will generate maximum four edges with label 0 and minimum six edges with label 1. That is,
the possible assignment of labels to adjacent vertices will be (1,2), (1,3), (1,4), (1,5), (1,6), (2,3), (2,4), (2,5), (2,6), (3,4), (3,5), (3,6), (4,5), (4,6), (5,6). Such assignment will generate maximum four edges with label 0 and minimum six edges with label 1. That is, . Hence
. Hence 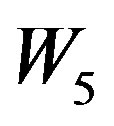 is not a prime cordial graph.
is not a prime cordial graph.
For the graph  the possible assignment of labels to adjacent vertices will be (1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (2,3), (2,4), (2,5), (2,6), (2,7), (3,4), (3,5), (3,6), (3,7), (4,5), (4,6), (4,7), (5,6), (5,7), (6,7). Such assignment will generate maximum four edges with label 0 and minimum eight edges with label 1. That is,
the possible assignment of labels to adjacent vertices will be (1,2), (1,3), (1,4), (1,5), (1,6), (1,7), (2,3), (2,4), (2,5), (2,6), (2,7), (3,4), (3,5), (3,6), (3,7), (4,5), (4,6), (4,7), (5,6), (5,7), (6,7). Such assignment will generate maximum four edges with label 0 and minimum eight edges with label 1. That is,  . Hence
. Hence  is not a prime cordial graph.
is not a prime cordial graph.
Now in  to satisfy the edge condition for prime cordial labeling it is essential to label seven edges with label 0 and seven edges with label 1 out of fourteen edges. But all the possible assignments of vertex labels will give rise to 0 labels for at most six edges and 1 labels for at least eight edges. That is,
to satisfy the edge condition for prime cordial labeling it is essential to label seven edges with label 0 and seven edges with label 1 out of fourteen edges. But all the possible assignments of vertex labels will give rise to 0 labels for at most six edges and 1 labels for at least eight edges. That is,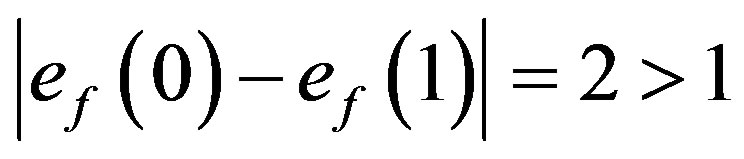 . Hence
. Hence  is not a prime cordial graph.
is not a prime cordial graph.
Hence Wn is not a prime cordial graph for n = 3 to n = 7.
Theorem 2.11  is a prime cordial graph for
is a prime cordial graph for .
.
Proof: Let  be the apex vertex of wheel
be the apex vertex of wheel  and
and  be the rim vertices. To define
be the rim vertices. To define 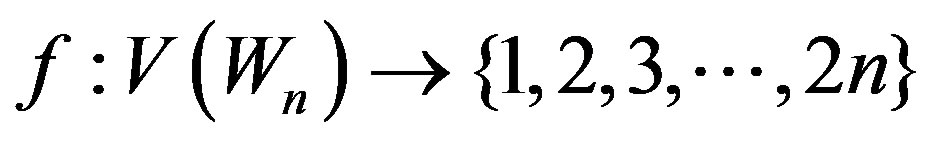 , we consider the following three cases.
, we consider the following three cases.
Case 1: n = 8,9,10 The graphs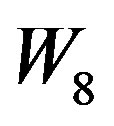 ,
,  and
and  are to be dealt separately and their prime cordial labeling is shown Figure 7.
are to be dealt separately and their prime cordial labeling is shown Figure 7.
Case 2:  is even,
is even, 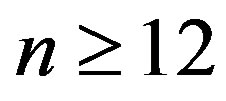
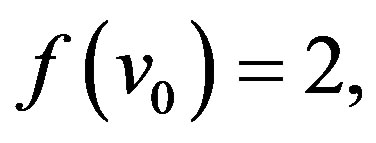



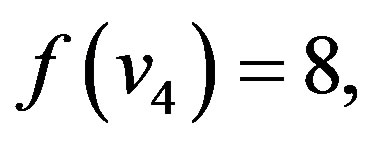
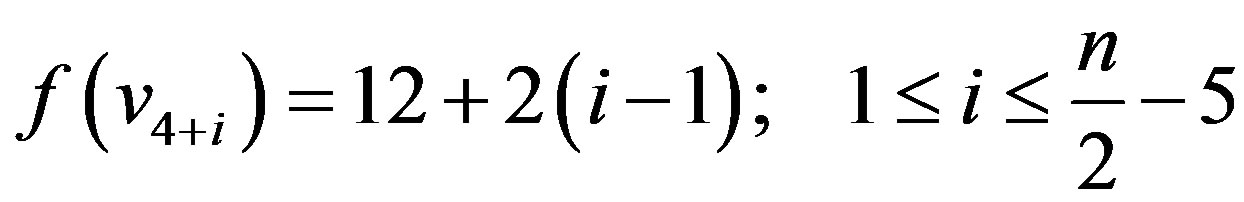
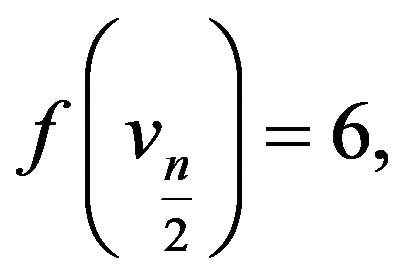



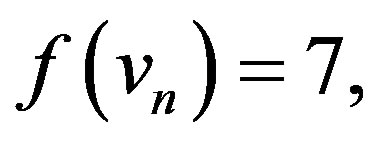

In view of the above defined labeling pattern we have 
Case 3: 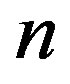 is odd,
is odd, 
In view of the above defined labeling pattern we have 
Thus in all the cases we have .
.
Hence  is a prime cordial graph for
is a prime cordial graph for .
.
Illustration 2.12 Prime cordial labeling of the graph  is shown in Figure 8.
is shown in Figure 8.
3. Concluding Remarks
As not every graph admit prime cordial labeling it is very interesting to investigate graph or graph families which admit prime cordial labeling. In this paper we have investigated some new prime cordial graphs. To investigate similar results for other graph families as well as in the context of different labeling problems is an open area of research.

Figure 8.  and its prime cordial labelling.
and its prime cordial labelling.