How Classical, Quantum-Mechanical, and Relativistic Wave and Field Equations Are Uniformly Generated by Velocity-Field Divergence Equations

Frank Blume

Department of Mathematics, John Brown University, Siloam Springs, USA.

DOI: 10.4236/jamp.2023.119178                

Abstract

We expand previously established results concerning the uniform representability of classical and relativistic gravitational field equations by means of velocity-field divergence equations by demonstrating that conservation equations for (probability) density functions give rise to velocity-field divergence equations the solutions of which generate—by way of superposition—the totality of solutions of various well-known classical and quantum-mechanical wave equations.

Keywords

Uniform Representability, Gravitational Field Equations, Velocity-Field Divergence Equations, Conservation Equations, Wave Equations

1. Introduction

The purpose of this paper is to broaden the scope of the results established in [1] and [2] by demonstrating that the notion of the divergence of a classical-motion velocity field generates a unifying mathematical description of various prominent wave and field equations of theoretical physics. To this end, we will show, in Sections 2, 3, 4, 5, and 6, how solutions of the Klein-Gordon equation, the Schrödinger equation, and the classical wave equation can be obtained by superimposing wave functions $\psi$ that in turn produce solutions $\rho$ of the (probability) preservation equation

$\begin{array}{c}\text{div}\left(\rho v\right)=0\end{array}$ (1)

by way of the defining equation

$\begin{array}{c}\rho \mathrm{<mo>\; :\; </mo>}=\sqrt{{\psi }^{\mathrm{<mo>\; *\; </mo>}}\psi }\mathrm{.}\end{array}$ (2)

That said, we must hasten to add that in our above-designation of Equation (1) as a “(probability) preservation equation”, we placed the word “probability” in parentheses because the interpretation of $\rho$ as a probability density function is not at all essential to our overall purpose. In particular, this suggested interpretation is not meant to contradict the well-known fact that there is no general probability preservation equation associated with the Klein-Gordon equation—nor is it meant to introduce a competing notion of probability preservation to non-relativistic quantum mechanics where the probability density function is commonly defined to be the product ${\psi }^{\mathrm{<mo>\; *\; </mo>}}\psi$ rather than the square root of that product (as suggested in (2)). What we are after, first and foremost, is not physical interpretive novelty but the bringing to light of an underlying mathematical unity.

In order to make more precise the role played by Equation (1) in generating solutions of the various wave equations, referred to above, it is helpful to observe that $\rho$ , as defined in (2), is a solution of (1) whenever there exists a real-valued function L (which we will choose to be the Lagrangian of a particle that moves with velocity $v$ ) such that the wave function $\psi$ in (2) is a solution of the first-order wave equation

$\begin{array}{c}\text{div}\left(\psi v\right)=\pm iL\psi \mathrm{.}\end{array}$ (3)

This is so because (3) implies that

$\begin{array}{c}\text{div}\left(\rho v\right)=v\left[\rho \right]+\rho \text{div}v=\frac{{\psi }^{\mathrm{<mo>\; *\; </mo>}}v\left[\psi \right]+\psi v\left[{\psi }^{\mathrm{<mo>\; *\; </mo>}}\right]}{2\rho }+\rho \text{div}v\\ =\frac{{\psi }^{\mathrm{<mo>\; *\; </mo>}}\left(-\psi \text{div}v\pm iL\psi \right)+\psi \left(-{\psi }^{\mathrm{<mo>\; *\; </mo>}}\text{div}v\mp iL{\psi }^{\mathrm{<mo>\; *\; </mo>}}\right)}{2\rho }+\rho \text{div}v\\ =-\frac{{\psi }^{\mathrm{<mo>\; *\; </mo>}}\psi \text{div}v}{\rho }+\rho \text{div}v=\mathrm{0,}\end{array}$

where the brackets indicate, as usual, the taking of the directional derivative, that is, $v\left[\psi \right]={\partial }_v\psi$ . So it is the establishment of this link between Equations (1) and (3) that happens to necessitate—for purely technical reasons—the introduction of the square root in (2), and it is this link as well that validates our pertinent claim according to which Equation (1) uniformly facilitates the construction of the sets of solutions of the various wave equations that we will subsequently discuss. As we will see, it is in superimposing solutions of Equation (3) that we will be able to generate these sets of solutions.

Moreover, in reference to the results established in [2] , it is worth mentioning that in a certain prominent special case the preservation Equation (1) is equivalent to the familiar relativistic preservation equation which asserts the divergence of the stress-energy tensor $T$ to be zero. To see why this is so, we assume that the curvature of a spacetime manifold is induced by the gravitational interactions of a swarm of free particles whose rest-frame mass density is $\rho$ and whose unit-length geodesic velocity field is $u$ (i.e., ${\nabla }_{u}u=0$ and $g\left(u\mathrm{,}u\right)=1$ ). In other words, we assume that the stress-energy tensor is

$\rho u\otimes u\mathrm{,}$

or equivalently, that

$T\left(v\right)=\rho g\left(v\mathrm{,}u\right)u\mathrm{.}$

Given this assumption, the vanishing of the divergence of $T$ is equivalent to the validity of the conservation equation

$\text{div}\left(\rho u\right)=0$

because in using the geodesic equation ${\nabla }_{u}u=0$ , we find that

$\begin{array}{c}\text{div}T\left(v\right)=g\left(\left({\nabla }_{e_{\mu }}T\right)\left(v\right)\mathrm{,}{e}^{\mu }\right)\\ =g\left({\nabla }_{e_{\mu }}T\left(v\right)\mathrm{,}{e}^{\mu }\right)-g\left(T\left({\nabla }_{e_{\mu }}v\right)\mathrm{,}{e}^{\mu }\right)\\ =u\left[\rho g\left(u\mathrm{,}v\right)\right]+\rho g\left(u\mathrm{,}v\right)g\left({\nabla }_{e_{\mu }}u\mathrm{,}{e}^{\mu }\right)-\rho g\left(u\mathrm{,}{\nabla }_{u}v\right)\\ =\left(u\left[\rho \right]+\rho \text{div}\left(u\right)\right)g\left(u\mathrm{,}v\right)\\ =\text{div}\left(\rho u\right)g\left(u\mathrm{,}v\right)\end{array}$

for all tangent vector fields $v$ . Hence

$\text{div}T=0\iff \text{div}\left(\rho u\right)=\mathrm{0,}$ (4)

as desired.

The summative table below shows, in its last five rows, the results established in [2] along with the equivalence (4), and it also shows, in its first five rows, the results that we are going to derive in Sections 2, 3, 4, 5 and 6. Given this tabular summary, it does seem fair to assert that the notion of a (geodesic) velocity field yields surprisingly coherent mathematical descriptions of seemingly disparate fields of theoretical physics.

where

$s=\frac{1}{2mi}\left({\psi }^{\mathrm{<mo>\; *\; </mo>}}\frac{\partial \psi }{\partial x}-\psi \frac{\partial {\psi }^{\mathrm{<mo>\; *\; </mo>}}}{\partial x}\right)$ .

To better understand the motivating rationale for the mathematical methods outlined in this paper, it is helpful to appeal—at a purely intuitive level—to the quantum-mechanical wave-particle duality and to imagine each point of a classical or quantum-mechanical wave front to be the point of origin of a bundle of velocity-field trajectories that a particle might trace. Since the preservation of probability or mass along any such a bundle is guaranteed by Equation (1), it may occur to us to ask whether the corresponding density functions $\rho$ —one for each bundle—can perhaps be used to construct the solutions of the partial differential equation that describes the time-evolution of the wave front. So as we set $\rho$ equal to $\sqrt{{\psi }^{\mathrm{<mo>\; *\; </mo>}}\psi }$ and as we further observe that $\rho$ is a solution of (1) whenever $\psi$ is a solution of (3), we are naturally led to inquire whether the solution of the governing partial differential equation can be constructed by superimposing solutions of Equation (3). As it turns out, in all the examples discussed in this paper such a construction is indeed feasible, but the more general question concerning the classification of partial differential equations that allow for such a construction of solutions has yet to be answered.

In regard to this open question, however, we need to be aware that the unifying role played by velocity-field divergence equations is to some extent merely formal in nature. For the larger conceptual framework of which Equation (3) is descriptive, in the various examples discussed in this paper, is not at all uniform. In the case of the relativistic Klein-Gordon equation, all speeds along velocity-field trajectories are less than 1 (the speed of light), and the attendant pattern of superposition is therefore notably distinct from the one employed in solving the non-relativistic Schrödinger equation. Moreover, in the case of the classical wave equation, the speed along trajectories is prescribed to be uniformly equal to the constant wave propagation speed, and in order for the concept of a velocity-field divergence to be viable in this case, it must pertain to fields along velocity cones whose dimension is strictly smaller than that of the embedding Newtonian spacetime. So the generating Equation (3), while formally constant, does vary significantly, from one example to the next, in terms of its conceptual and physical interpretation.

So in the light of this interpretive variability, it is not at all obvious what a generalized theory concerning the constructability of solutions of partial differential equations from solutions of velocity-field divergence equations can be expected to look like. The constructions outlined in this paper are very much dependent for their technical specifics upon the larger physical context of which a given partial differential equation is descriptive. And by implication, a truly general theory that equally applies to all these different contexts may not be easy to create.

To conclude this introductory section, we wish to add, as a note of caution, that all the results derived in the present paper (as well as those derived in [1] and [2] ) appear to be quite elementary in character. Thus it is conceivable, and maybe even likely, that other authors have recorded them in prior publications. But since the present author is not aware of any pertinent reference, the results in question are here being offered—with considerable hesitation—as provisional novelties. Moreover, the claim to novelty here in question strictly pertains to the unifying role played by velocity-field divergence equations. So we are not asserting that the methods outlined in this paper are better than the standard methods described in, for example [3] - [10] , but merely that they are more uniform.

2. The Klein-Gordon Equation

In this section we will show how the full set of solutions of the Klein-Gordon equation in one spatial dimension,

$\begin{array}{c}\frac{{\partial }^2\psi }{\partial t^2}-\frac{{\partial }^2\psi }{\partial x^2}+m^2\psi =\mathrm{0,}\end{array}$

can be constructed by superimposing solutions of Equation (3). The restriction to one spatial dimension is a choice of convenience and is justified by the fact that the extension to two and then three spatial dimensions would employ methods similar to those used in Section 5 in solving the classical wave equation in two spatial dimensions.

To get started, we introduce, for all $y\in ℝ$ , all $t>0$ , and all $x\in \left(y-t\mathrm{,}y+t\right)$ the unit Lorentz vector

$u_y\left(t\mathrm{,}x\right)\mathrm{<mo>\; :\; </mo>}=\frac{1}{\sqrt{t^2-{\left(x-y\right)}^2}}\left(\begin{array}{c}t\\ x-y\end{array}\right)$ . (5)

and consider—in direct analogy to (3)—the first-order wave equation

$\text{div}\left({\psi }_y{u}_y\right)=u_y\left[{\psi }_y\right]+{\psi }_y\text{div}{u}_y=\pm i{L}_y{\psi }_y\mathrm{.}$ (6)

The plus-or-minus sign on the right may be considered to be directly expressive of the well-known fact that the Klein-Gordon equation has positive- and negative-energy solutions, but it may also be viewed to be a purely mathematical characteristic that naturally leads us to break up (6) into two distinct equations the solutions of which we will denote by ${\psi }_y^{+}$ and ${\psi }_y^{-}$ , respectively. As we will see, this flexibility will be needed in order to generate the full set of solutions of the Klein-Gordon equation.

To proceed, we observe that the Lagrangian $L_y$ of a free particle that moves along the unit-velocity flow line

$c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\mathrm{<mo>\; :\; </mo>}=\left(\begin{array}{c}0\\ y\end{array}\right)+s{u}_y\left(t\mathrm{,}x\right)$

is equal to the particle’s rest mass m (in the particle’s rest frame and in Planck units) and that

$\text{div}{u}_y\left(t\mathrm{,}x\right)=\frac{\partial }{\partial t}\frac{t}{\sqrt{t^2-{\left(x-y\right)}^2}}+\frac{\partial }{\partial x}\frac{x-y}{\sqrt{t^2-{\left(x-y\right)}^2}}=\frac{1}{\sqrt{t^2-{\left(x-y\right)}^2}}\mathrm{.}$

According to Equation (6), this yields

${u_y\left[{\psi }_y^{+}\right]|}_{\left(t\mathrm{,}x\right)}=-\frac{{\psi }_y^{+}}{\sqrt{t^2-{\left(x-y\right)}^2}}+im{\psi }_y^{+}=-\frac{{\psi }_y^{+}}{\Vert \left(\begin{array}{c}t\\ x-y\end{array}\right)\Vert }+im{\psi }_y^{+}\mathrm{,}$

and, by implication,

$\begin{array}{c}\frac{\text{d}}{\text{d}s}{\psi }_y^{+}\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)={c^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\left[{\psi }_y^{+}\right]={-\frac{{\psi }_y^{+}}{\Vert \left(\begin{array}{c}t\\ x-y\end{array}\right)\Vert }|}_{c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)}+im{\psi }_y^{+}\\ =-\frac{{\psi }_y^{+}}{\Vert s{u}_y\left(t\mathrm{,}x\right)\Vert }+im{\psi }_y^{+}=\left(-\frac{1}{s}+im\right){\psi }_y^{+}.\end{array}$

One possible solution of this equation is easily seen to be

${\psi }_y^{+}\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)=\frac{{\text{e}}^{ims}}{\pi s}$ ,

and in setting $s=\sqrt{t^2-{\left(x-y\right)}^2}$ , we find the following Lorentz-invariant form of the wave function ${\psi }_y^{+}$ :

${\psi }_y^{+}\left(t,x\right)=\frac{{\text{e}}^{im\sqrt{t^2-{\left(x-y\right)}^2}}}{\pi \sqrt{t^2-{\left(x-y\right)}^2}}=\frac{{\text{e}}^{imt\sqrt{1-{\left(x-y\right)}^2/t^2}}}{\pi t\sqrt{1-{\left(x-y\right)}^2/t^2}}.$ (7)

By analogy, we also find that

${\psi }_y^{-}\left(t\mathrm{,}x\right)=\frac{{\text{e}}^{-imt\sqrt{1-{\left(x-y\right)}^2/t^2}}}{\pi t\sqrt{1-{\left(x-y\right)}^2/t^2}}\mathrm{.}$ (8)

Remark. The factor $1/\pi$ is a normalizing constant that guarantees that the integral of the density ${\rho }_y=\sqrt{{\psi }^{+}{}^{\ast }{\psi }^{+}}=\sqrt{{\psi }^{-}{}^{\ast }{\psi }^{-}}$ over any plane spatial cross-section of the light cone $\left\{\left(t,x\right)|t>0\wedge y-t<x<y+t\right\}$ is always equal to one:

${\displaystyle {\int }_{y-t}^{y+t}}{\rho }_y\left(t\mathrm{,}x\right)\text{d}x={\displaystyle {\int }_{y-t}^{y+t}}\frac{1}{\pi t\sqrt{1-{\left(x-y\right)}^2/t^2}}\text{d}x={\displaystyle {\int }_{-1}^1}\frac{1}{\pi \sqrt{1-v^2}}\text{d}v=1.$

In order to generate the full set of solutions of the Klein-Gordon equation, we will now superimpose the solutions ${\psi }_y^{+}$ and ${\psi }_y^{-}$ as given in (7) and (8). To do so, we notice that

$u_y\left(t\mathrm{,}x\right)\left[\frac{x-y}{t}\right]=0$

and that therefore

$h^{+}\left(y\mathrm{,}\frac{x-y}{t}\right){\psi }_y^{+}\left(t,x\right)$

and

$h^{-}\left(y\mathrm{,}\frac{x-y}{t}\right){\psi }_y^{-}\left(t,x\right)$

are solutions of (6) for any complex-valued differentiable functions $h^{+}\left(y\mathrm{,}v\right)$ and $h^{-}\left(y\mathrm{,}v\right)$ . Hence we may attempt to find a solution $\psi$ of the Klein-Gordon equation of the following form:

$\begin{array}{c}\psi \left(t,x\right)={\displaystyle {\int }_{x-t}^{x+t}}\left(h^{+}\left(y,\frac{x-y}{t}\right){\psi }_y^{+}\left(t,x\right)+h^{-}\left(y,\frac{x-y}{t}\right){\psi }_y^{-}\left(t,x\right)\right)\text{d}y\\ ={\displaystyle {\int }_{-1}^1}\left(\frac{h^{+}\left(x-vt,v\right){\text{e}}^{imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}+\frac{h^{-}\left(x-vt,v\right){\text{e}}^{-imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}\right)\text{d}v.\end{array}$ (9)

(Note: the substitution $v=\left(x-y\right)/t$ causes the factor 1/t in (7) and (8) to disappear.) Using elementary rules of differentiation, it follows that

$\begin{array}{c}\frac{{\partial }^2\psi }{\partial t^2}={\displaystyle {\int }_{-1}^1}\left(v^2\frac{{\partial }^2{h}^{+}}{\partial y^2}\left(x-vt,v\right)-2imv\sqrt{1-v^2}\frac{\partial h^{+}}{\partial y}\left(x-vt,v\right)\right)\frac{{\text{e}}^{imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}\text{d}v\\ -m^2{\displaystyle {\int }_{-1}^1}\left(1-v^2\right)h^{+}\left(x-vt,v\right)\frac{{\text{e}}^{imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}\text{d}v\\ +{\displaystyle {\int }_{-1}^1}\left(v^2\frac{{\partial }^2{h}^{-}}{\partial y^2}\left(x-vt,v\right)+2imv\sqrt{1-v^2}\frac{\partial h^{-}}{\partial y}\left(x-vt,v\right)\right)\frac{{\text{e}}^{-imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}\text{d}v\\ -m^2{\displaystyle {\int }_{-1}^1}\left(1-v^2\right)h^{-}\left(x-vt,v\right)\frac{{\text{e}}^{-imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}\text{d}v\end{array}$

and

$\frac{{\partial }^2\psi }{\partial x^2}={\displaystyle {\int }_{-1}^1}\left(\frac{{\partial }^2{h}^{+}}{\partial y^2}\left(x-vt,v\right)\frac{{\text{e}}^{imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}+\frac{{\partial }^2{h}^{-}}{\partial y^2}\left(x-vt,v\right)\frac{{\text{e}}^{-imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}\right)\text{d}v.$

Hence

$\begin{array}{l}\frac{{\partial }^2\psi }{\partial t^2}-\frac{{\partial }^2\psi }{\partial x^2}+m^2\psi \\ ={\displaystyle {\int }_{-1}^1}\left(-\left(1-v^2\right)\frac{{\partial }^2{h}^{+}}{\partial y^2}-2imv\sqrt{1-v^2}\frac{\partial h^{+}}{\partial y}+m^2{v}^2{h}^{+}\right)\frac{{\text{e}}^{imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}\text{d}v\\ +{\displaystyle {\int }_{-1}^1}\left(-\left(1-v^2\right)\frac{{\partial }^2{h}^{-}}{\partial y^2}+2imv\sqrt{1-v^2}\frac{\partial h^{-}}{\partial y}+m^2{v}^2{h}^{-}\right)\frac{{\text{e}}^{-imt\sqrt{1-v^2}}}{\pi \sqrt{1-v^2}}\text{d}v,\end{array}$

and, in setting $z_v^{\pm }\left(y\right)\mathrm{<mo>\; :\; </mo>}=h^{\pm }\left(y\mathrm{,}v\right)$ , we may thus infer that $\psi$ is a solution of the Klein-Gordon equation if $z_v^{\pm }$ is a solution of the following second-order linear homogeneous differential equation:

${z^{\prime }}^{\prime }\left(y\right)\pm \frac{2imv{z}^{\prime }\left(y\right)}{\sqrt{1-v^2}}-\frac{m^2{v}^{2}z\left(y\right)}{1-v^2}=0.$

Since the characteristic polynomial of this equation is

$x^2\pm \frac{2imvx}{\sqrt{1-v^2}}-\frac{m^2{v}^2}{1-v^2}={\left(x\pm \frac{imv}{\sqrt{1-v^2}}\right)}^2,$

it follows that there are coefficient functions $C_1^{\pm }\left(v\right)$ and $C_2^{\pm }\left(v\right)$ such that

$h^{\pm }\left(y,v\right)=z_v^{\pm }\left(y\right)=C_1^{\pm }\left(v\right){\text{e}}^{\mp imvy/\sqrt{1-v^2}}+C_2^{\pm }\left(v\right)y{\text{e}}^{\mp imvy/\sqrt{1-v^2}}.$

Upon closer examination, we find that the added flexibility which the second term on the right-hand side of this equation seemingly provides is actually inconsequential. That is to say, the inclusion of this term does not increase the size of the set of solutions $\psi$ (as a few simple calculations would readily show). Thus we will set $C_2^{\pm }:=0$ and write $C^{\pm }$ instead of $C_1^{\pm }$ . This yields the following form of the general solution of the Klein-Gordon equation:

$\boxed{\psi \left(t,x\right)=\frac{1}{\pi }{\displaystyle {\int }_{-1}^1}\left(C^{+}\left(v\right)\frac{{\text{e}}^{im\left(t-vx\right)/\sqrt{1-v^2}}}{\sqrt{1-v^2}}+C^{-}\left(v\right)\frac{{\text{e}}^{-im\left(t-vx\right)/\sqrt{1-v^2}}}{\sqrt{1-v^2}}\right)\text{d}v.}$

The fact that any function of this form is indeed a solution of the Klein-Gordon equation follows from the preceding discussion and can of course also be verified directly by means of straightforward differentiation. Consequently, in order to prove that the functions $\psi$ , given above, exhaust the full set of solutions of the Klein-Gordon equation, it only remains to be shown that the coefficient functions $C^{+}$ and $C^{-}$ can be determined from the initial conditions

$\psi \left(0,x\right)=\frac{1}{\pi }{\displaystyle {\int }_{-1}^1}\left(C^{+}\left(v\right)\frac{{\text{e}}^{-imvx/\sqrt{1-v^2}}}{\sqrt{1-v^2}}+C^{-}\left(v\right)\frac{{\text{e}}^{imvx/\sqrt{1-v^2}}}{\sqrt{1-v^2}}\right)\text{d}v.$ (10)

and

$\frac{\partial \psi }{\partial t}\left(0,x\right)=\frac{im}{\pi }{\displaystyle {\int }_{-1}^1}\left(C^{+}\left(v\right)\frac{{\text{e}}^{-imvx/\sqrt{1-v^2}}}{1-v^2}-C^{-}\left(v\right)\frac{{\text{e}}^{imvx/\sqrt{1-v^2}}}{1-v^2}\right)\text{d}v.$ (11)

To this end we introduce the additional substitution $k=mv/\sqrt{1-v^2}$ . This yields $v=k/\sqrt{m^2+k^2}=:k/f\left(k\right)$ , $1-v^2=m^2/f{\left(k\right)}^2$ , $\text{d}v=m^2\text{d}k/f{\left(k\right)}^3$ ,

$\begin{array}{c}\psi \left(0,x\right)=\frac{m}{\pi }{\displaystyle {\int }_{-\infty }^{\infty }}\left(C^{+}\left(\frac{k}{f\left(k\right)}\right)\frac{{\text{e}}^{-ikx}}{f{\left(k\right)}^2}+C^{-}\left(\frac{k}{f\left(k\right)}\right)\frac{{\text{e}}^{ikx}}{f{\left(k\right)}^2}\right)\text{d}k\\ =\frac{m}{\pi }{\displaystyle {\int }_{-\infty }^{\infty }}\left(C^{+}\left(\frac{-k}{f\left(k\right)}\right)+C^{-}\left(\frac{k}{f\left(k\right)}\right)\right)\frac{{\text{e}}^{ikx}}{f{\left(k\right)}^2}\text{d}k,\end{array}$

and

$\begin{array}{c}\frac{\partial \psi }{\partial t}\left(0,x\right)=\frac{im}{\pi }{\displaystyle {\int }_{-\infty }^{\infty }}\left(C^{+}\left(\frac{k}{f\left(k\right)}\right)\frac{{\text{e}}^{-ikx}}{f\left(k\right)}-C^{-}\left(\frac{k}{f\left(k\right)}\right)\frac{{\text{e}}^{ikx}}{f\left(k\right)}\right)\text{d}k\\ =\frac{im}{\pi }{\displaystyle {\int }_{-\infty }^{\infty }}\left(C^{+}\left(\frac{-k}{f\left(k\right)}\right)-C^{-}\left(\frac{k}{f\left(k\right)}\right)\right)\frac{{\text{e}}^{ikx}}{f\left(k\right)}\text{d}k.\end{array}$

Setting $B^{+}\left(k\right)\mathrm{<mo>\; :\; </mo>}=2m{C}^{+}\left(-k/f\left(k\right)\right)/f{\left(k\right)}^2$ and $B^{-}\left(k\right)\mathrm{<mo>\; :\; </mo>}=2m{C}^{-}\left(k/f\left(k\right)\right)/f{\left(k\right)}^2$ , we obtain

$\psi \left(0,x\right)=\frac{1}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }\left(B^{+}\left(k\right)+B^{-}\left(k\right)\right){\text{e}}^{ikx}\text{d}k}$

and

$\frac{\partial \psi }{\partial t}\left(0,x\right)=\frac{i}{2\pi }{\displaystyle {\int }_{-\infty }^{\infty }f}\left(k\right)\left(B^{+}\left(k\right)-B^{-}\left(k\right)\right){\text{e}}^{ikx}\text{d}k.$

Thus, by Fourier inversion,

$B^{+}\left(k\right)+B^{-}\left(k\right)={\displaystyle {\int }_{-\infty }^{\infty }\psi }\left(0,x\right){\text{e}}^{-ikx}\text{d}x$

and

$if\left(k\right)\left(B^{+}\left(k\right)-B^{-}\left(k\right)\right)={\displaystyle {\int }_{-\infty }^{\infty }\frac{\partial \psi }{\partial t}}\left(0,x\right){\text{e}}^{-ikx}\text{d}x.$

In solving these two equations for $B^{+}\left(k\right)$ and $B^{-}\left(k\right)$ —and determining $C^{+}$ and $C^{-}$ thereby—we may conclude that the initial conditions (10) and (11) can indeed always be satisfied by properly choosing the coefficient functions $C^{+}$ and $C^{-}$ .

3. The Free-Particle Schrödinger Equation

Since the free-particle Schrödinger equation,

$\boxed{i\frac{\partial \psi }{\partial t}=-\frac{1}{2m}\frac{{\partial }^2\psi }{\partial x^2},}$

turns out to be considerably easier to deal with than the general Schrödinger Equation (with a non-zero potential), it may be instructive and helpful to first examine only this simpler equation and then to move on, in the next section, to the more involved calculations that the general Schrödinger equation gives rise to. Since the Schrödinger equation is non-relativistic in nature, we replace the relativistic unit field $u_y$ , as defined in (5), by the non-relativistic field

$v_y\left(t,x\right):=\left(\begin{array}{c}1\\ v_y\left(t,x\right)\end{array}\right):=\left(\begin{array}{c}1\\ \left(x-y\right)/t\end{array}\right)$

and consider the corresponding wave equation

$\text{div}\left({\psi }_y{v}_y\right)=v_y\left[{\psi }_y\right]+{\psi }_y\text{div}{v}_y=i{L}_y{\psi }_y$ (12)

with

$L_y\left(t,x\right)=\frac{m{v}_y^2\left(t,x\right)}{2}=\frac{m}{2}{\left(\frac{x-y}{t}\right)}^2.$

(Note: the reason why, in (12), we wrote $i{L}_y$ instead of $\pm i{L}_y$ is that the Schrödinger equation is first-order in t and therefore requires less flexibility in adjusting its solutions to given initial conditions.) Setting

$c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\mathrm{<mo>\; :\; </mo>}=\left(\begin{array}{c}0\\ y\end{array}\right)+s{v}_y\left(t\mathrm{,}x\right)$

and noting that

$\text{div}{v}_y\left(t\mathrm{,}x\right)=\frac{\partial }{\partial x}\frac{x-y}{t}=\frac{1}{t}\mathrm{,}$

we may apply (12) to infer that

${v_y\left[{\psi }_y\right]|}_{\left(t\mathrm{,}x\right)}=-\frac{{\psi }_y}{t}+\frac{im}{2}{\left(\frac{x-y}{t}\right)}^2{\psi }_y\mathrm{.}$

Thus

$\begin{array}{c}\frac{\text{d}}{\text{d}s}{\psi }_y\left(c_{y,t,x}\left(s\right)\right)={c^{\prime }}_{y,t,x}\left(s\right)\left[{\psi }_y\right]=-\frac{{\psi }_y}{s}+\frac{im{v}_y\left(c_{y,t,x}\left(s\right)\right)}{2}{\psi }_y\\ =-\frac{{\psi }_y}{s}+\frac{im}{2}{\left(\frac{s\left(x-y\right)/t}{s}\right)}^2{\psi }_y\\ =-\frac{1}{s}+\frac{im}{2}{\left(\frac{x-y}{t}\right)}^2{\psi }_y,\end{array}$

and one possible solution of this equation is

${\psi }_y\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)=\frac{{\text{e}}^{im{\left(x-y\right)}^{2}s/\left(2t^2\right)}}{s}\mathrm{.}$

Setting $s=t$ , yields

${\psi }_y\left(t\mathrm{,}x\right)=\frac{{\text{e}}^{im{\left(x-y\right)}^{2}t/\left(2t^2\right)}}{t}\mathrm{,}$ (13)

and, in direct analogy to (9), we may therefore conjecture the general solution of the free-particle Schrödinger equation to be of the following form:

$\psi \left(t,x\right)={\displaystyle {\int }_{-\infty }^{\infty }h}\left(y,\frac{x-y}{t}\right){\psi }_y\left(t,x\right)\text{d}y={\displaystyle {\int }_{-\infty }^{\infty }h}\left(x-vt,v\right){\text{e}}^{im{v}^{2}t/2}\text{d}v.$ (14)

(Note: here again the factor 1/t in (13) disappears due to the substitution $v=\left(x-y\right)/t$ .) Given this representation of $\psi \left(t\mathrm{,}x\right)$ , we readily find that

$\frac{\partial \psi }{\partial t}={\displaystyle {\int }_{-\infty }^{\infty }\left(-v\frac{\partial h}{\partial y}\left(x-vt,v\right)+\frac{im{v}^2}{2}h\left(x-vt,v\right)\right){\text{e}}^{im{v}^{2}t/2}\text{d}v}$

and

$\frac{{\partial }^2\psi }{\partial x^2}={\displaystyle {\int }_{-\infty }^{\infty }\frac{{\partial }^{2}h}{\partial y^2}}\left(x-vt,v\right){\text{e}}^{im{v}^{2}t/2}\text{d}v.$

Hence

$i\frac{\partial \psi }{\partial t}+\frac{1}{2m}\frac{{\partial }^2\psi }{\partial x^2}={\displaystyle {\int }_{-\infty }^{\infty }\left(\frac{1}{2m}\frac{{\partial }^{2}h}{\partial y^2}-iv\frac{\partial h}{\partial y}-\frac{m{v}^{2}h}{2}\right){\text{e}}^{im{v}^{2}t/2}\text{d}v},$

and therefore, $\psi$ is a solution of the free-particle Schrödinger equation if $z_v\left(y\right):=h\left(y,v\right)$ is a solution of the differential equation

$z^{″}\left(y\right)-2imv{z}^{\prime }\left(y\right)-m^2{v}^{2}z\left(y\right)=0.$

Since the characteristic polynomial of this equation is

$x^2-2imvx-m^2{v}^2={\left(x-imv\right)}^2,$

it follows that there are coefficient functions $C_1\left(v\right)$ and $C_2\left(v\right)$ such that

$h\left(y,v\right)=z_v\left(y\right)=C_1\left(v\right){\text{e}}^{imvy}+C_2\left(v\right)y{\text{e}}^{imvy}.$

As in the previous section, the second term on the right turns out to be redundant, and therefore, we may write

$h\left(y,v\right)=C\left(v\right){\text{e}}^{imvy}.$

Using (14), it readily follows that

$\boxed{\psi \left(t,x\right)={\displaystyle {\int }_{-\infty }^{\infty }C}\left(v\right){\text{e}}^{-im\left(v^{2}t/2-vx\right)}\text{d}v,}$

and the single initial condition

$\psi \left(0,x\right)={\displaystyle {\int }_{-\infty }^{\infty }C}\left(v\right){\text{e}}^{imvx}\text{d}v$

can easily be met, as in the previous section, by determining $C\left(v\right)$ via Fourier inversion.

4. The General Schrödinger Equation

Before we move on to apply the methods used in the preceding two sections to the general Schrödinger equation,

$\boxed{i\frac{\partial \psi }{\partial t}=-\frac{1}{2m}\frac{{\partial }^2\psi }{\partial x^2}+V\left(x\right)\psi ,}$

we need to briefly review the results established in [1] . To do so, we denote by $z_{y,t,x}$ the spatial coordinate of a classical particle of mass m that moves in one spatial dimension in the force field $F=-\nabla V$ and satisfies the boundary conditions

$z_{y,t,x}\left(0\right)=y$ (15)

and

$z_{y,t,x}\left(t\right)=x.$ (16)

Given this definition of $z_{y\mathrm{,}t\mathrm{,}x}$ , the corresponding 2-velocity field $v_y$ is

$v_y\left(t\mathrm{,}x\right)=\left(\begin{array}{c}1\\ {z^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(t\right)\end{array}\right)=\mathrm{<mo>\; :\; </mo>}\left(\begin{array}{c}1\\ v_y\left(t\mathrm{,}x\right)\end{array}\right)$

and the flow lines of $v_y$ are described, in dependence on t and x, by the parameterizations

$c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\mathrm{<mo>\; :\; </mo>}=\left(\begin{array}{c}s\\ z_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\end{array}\right)\mathrm{.}$

As explained in [1] (and as we will further explain below), it is plausible and necessary to assume that there is a value $T>0$ such that the boundary conditions (15) and (16) uniquely determine $z_{y\mathrm{,}t\mathrm{,}x}$ for all $t\in \left(\mathrm{0,}T\right)$ . For only under this assumption does it follow that $v_y$ is a well defined vector field on $\left(\mathrm{0,}T\right)\times ℝ$ for all $y\in ℝ$ and that $c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)$ satisfies the flow line equation

${c^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(s\right)=v_y\left(c_{y\mathrm{,}t\mathrm{,}x}(\; s\; )\right)$

for all $s\in \left[\mathrm{0,}T\right)$ . After all, the unique determination of $z_{y\mathrm{,}t\mathrm{,}x}$ by the boundary conditions (15) and (16) implies that

$c_{y,t,x}\left(s\right)=c_{y,s,z_{y,t,x}\left(s\right)}\left(s\right)=c_{y,c_{y,t,x}\left(s\right)}\left(s\right),$ (17)

for all $s\in \left[\mathrm{0,}T\right)$ , and this equation in turn implies that

${c^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(s\right)=\left(\begin{array}{c}1\\ {z^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\end{array}\right)=\left(\begin{array}{c}1\\ {z^{\prime }}_{y\mathrm{,}{c}_{y\mathrm{,}t\mathrm{,}x}\left(s\right)}\left(s\right)\end{array}\right)=\left(\begin{array}{c}1\\ v_y\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)\end{array}\right)=v_y\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)\mathrm{.}$

Given this setup, we showed in [1] that the density function ${\rho }_y={\psi }_y^{*}{\psi }_y$ —without the square root—satisfies the preservation equation $\text{div}\left({\rho }_y{v}_y\right)=0$ whenever there exists a real-valued function $L_y$ such that ${\psi }_y$ is a solution of the first-order wave equation

$\text{div}\left({\psi }_y{v}_y\right)=\frac{{\psi }_y}{2}\text{div}{v}_y+i{L}_y{\psi }_y\mathrm{.}$ (18)

(Note: in this latter equation, the first term on the right had to be inserted in order to account for the omission of the square root in the definition of ${\rho }_y$ .) As demonstrated in [1] , any solution of the free-particle Schrödinger equation as well as the general Schrödinger equation with an harmonic-oscillator type potential

$V\left(x\right)=\alpha x^2+\beta x+\gamma$ (19)

can be obtained by superimposing solutions of Equation (18). Moreover, we also showed in [1] that for arbitrary potentials V the full set of solutions of the Schrödinger equation can be constructed by superimposing solutions of (18) along path-integrals (as in Feynman’s path-integral formalism).

Given these results, our goal in the present paper will be to show that the general Schrödinger equation—with V as defined in (19)—can also be solved by superimposing solutions of Equation (12) instead of Equation (18). So we will not discuss the most general case, using path-integrals, but limit ourselves to the discussion of the general Schrödinger equation with harmonic-oscillator type potentials. To be sure, the path-integral construction used in [1] can also be applied to solutions of Equation (12), but since the purpose of the present paper is not to discuss the Schrödinger equation in particular and in full detail but rather to bring to light a certain unifying principle, the simplifying restriction to harmonic-oscillator type potentials seems natural and permissible.

In order to begin the process of solving the Schrödinger equation, with V as defined in (19), we introduce the following lemma:

Lemma 4.1. There exist functions $a\left(t\mathrm{,}s\right)$ , $b\left(t\mathrm{,}s\right)$ , and $c\left(t\mathrm{,}s\right)$ such that

$z_{y\mathrm{,}t\mathrm{,}x}\left(s\right)=a\left(t\mathrm{,}s\right)x+b\left(t\mathrm{,}s\right)y+c\left(t\mathrm{,}s\right)$

for all $\left(y\mathrm{,}t\mathrm{,}x\mathrm{,}s\right)\in ℝ\times \left(\mathrm{0,}T\right)\times ℝ\times \left[\mathrm{0,}T\right)$ if and only if V is an harmonic-oscillator type potential, as given in (19).

Proof. “ $\Rightarrow$ ” If $z_{y\mathrm{,}t\mathrm{,}x}\left(s\right)=a\left(t\mathrm{,}s\right)x+b\left(t\mathrm{,}s\right)y+e\left(t\right)f\left(s\right)$ , then

$v_y\left(c_{y,t,x}\left(s\right)\right)={z^{\prime }}_{y,t,x}\left(s\right)=\frac{\partial a}{\partial s}\left(t,s\right)x+\frac{\partial b}{\partial s}\left(t,s\right)y+\frac{\partial c}{\partial s}\left(t,s\right),$

and

$v_y\left(t\mathrm{,}x\right)=\frac{\partial a}{\partial s}\left(t\mathrm{,}t\right)x+\frac{\partial b}{\partial s}\left(t\mathrm{,}t\right)y+\frac{\partial c}{\partial s}\left(t\mathrm{,}t\right)\mathrm{.}$

Consequently, in setting $p\left(t\right):=\partial a\left(t,t\right)/\partial s$ , $q\left(t\right):=\partial b\left(t,t\right)/\partial s$ , and $r\left(t\right):=\partial c\left(t,t\right)/\partial s$ , we may apply Newton’s law of motion to conclude that

$\begin{array}{c}-\frac{1}{m}{V}^{\prime }\left(x\right)=-\frac{1}{m}{V}^{\prime }\left(z_{y,t,x}\left(t\right)\right)={z^{″}}_{y,t,x}\left(t\right)={\frac{\text{d}}{\text{d}s}{v}_y\left(c_{y,t,x}\left(s\right)\right)|}_{s=t}={c^{\prime }}_{y,t,x}\left(t\right)\left[v_y\right]\\ =v_y\left(t\mathrm{,}x\right)\left[v_y\right]=\frac{\partial v_y}{\partial t}+v_y\left(t\mathrm{,}x\right)\frac{\partial v_y}{\partial x}\\ =p^{\prime }\left(t\right)x+q^{\prime }\left(t\right)y+r^{\prime }\left(t\right)+\left(p\left(t\right)x+q\left(t\right)y+r\left(t\right)\right)p\left(t\right)\\ =\left(p^{\prime }\left(t\right)+p{\left(t\right)}^2\right)x+\left(q^{\prime }\left(t\right)+q\left(t\right)p\left(t\right)\right)y+r^{\prime }\left(t\right)+r\left(t\right)p\left(t\right)\mathrm{.}\end{array}$

Since the left-hand side of this equation only depends on x, the same must be true for the right-hand side, and therefore, $q^{\prime }\left(t\right)+q\left(t\right)p\left(t\right)$ must equal zero, and the functions $p^{\prime }\left(t\right)+p{\left(t\right)}^2$ and $r^{\prime }\left(t\right)+r\left(t\right)p\left(t\right)$ must both be constant. In other words, there must exist constants $\alpha \mathrm{,}\beta \in ℝ$ such that

$V^{\prime }\left(x\right)=2\alpha x+\beta \mathrm{,}$

and this equation trivially implies that there is a value $\gamma \in ℝ$ such that

$V\left(x\right)=\alpha x^2+\beta x+\gamma \mathrm{,}$

as desired.

“ $\Leftarrow$ ” If $V\left(x\right)=\alpha x^2+\beta x+\gamma$ , then

$m{z^{″}}_{y,t,x}\left(s\right)=-V^{\prime }\left(z_{y,t,x}\left(s\right)\right)=-2\alpha z_{y,t,x}\left(s\right)-\beta ,$

and therefore, $z_{y\mathrm{,}t\mathrm{,}x}$ is a solution of the non-homogeneous second-order linear differential equation

$z^{″}\left(s\right)+\frac{2\alpha }{m}z\left(s\right)=-\frac{\beta }{m}\mathrm{.}$ (20)

According to the elementary theory of this kind of differential equation, there must exist a solution $g\left(s\right)$ of (20) and coefficients $C_1\left(y\mathrm{,}t\mathrm{,}x\right)$ and $C_2\left(y\mathrm{,}t\mathrm{,}x\right)$ such that for $\kappa \mathrm{<mo>\; :\; </mo>}=\sqrt{2\left|\alpha \right|/m}$ it is the case that either

$z_{y\mathrm{,}t\mathrm{,}x}\left(s\right)=C_1\left(y\mathrm{,}t\mathrm{,}x\right){\text{e}}^{\kappa s}+C_2\left(y\mathrm{,}t\mathrm{,}x\right){\text{e}}^{-\kappa s}+g\left(s\right)\left(\text{if}\alpha <0\right)$

or

$z_{y,t,x}\left(s\right)=C_1\left(y,t,x\right)\sin \left(\kappa s\right)+C_2\left(y,t,x\right)\cos \left(\kappa s\right)+g\left(s\right)\left(\text{if}\alpha >0\right)$

or

$z_{y,t,x}\left(s\right)=C_1\left(y,t,x\right)s+C_2\left(y,t,x\right)+g\left(s\right)\left(\text{if}\alpha =0\right).$

In the first two of these cases $g\left(s\right)$ can be chosen to be the constant $-\beta /2\alpha$ and in the third one it equals $-\beta s^2/\left(2m\right)$ . Given this observation, the boundary value conditions (15) and (16), readily imply (by way of some trivial calculations) that either

$z_{y,t,x}\left(s\right)=\frac{\sinh \left(\kappa s\right)}{\sinh \left(\kappa t\right)}\left(x+\frac{\beta }{2\alpha }\right)+\frac{\sinh \left(\kappa \left(t-s\right)\right)}{\sinh \left(\kappa t\right)}\left(y+\frac{\beta }{2\alpha }\right)-\frac{\beta }{2\alpha }\left(\text{if}\alpha <0\right)$

or

$z_{y,t,x}\left(s\right)=\frac{\sin \left(\kappa s\right)}{\sin \left(\kappa t\right)}\left(x+\frac{\beta }{2\alpha }\right)+\frac{\sin \left(\kappa \left(t-s\right)\right)}{\sin \left(\kappa t\right)}\left(y+\frac{\beta }{2\alpha }\right)-\frac{\beta }{2\alpha }\left(\text{if}\alpha >0\right)$

or

$z_{y,t,x}\left(s\right)=\frac{s}{t}\left(x+\frac{\beta t^2}{2m}\right)+\frac{t-s}{t}y-\frac{\beta s^2}{2m}\left(\text{if}\alpha =0\right).$

Consequently, in each of these cases there exist functions $a\left(t,s\right)$ , $b\left(t,s\right)$ , and $c\left(t,s\right)$ such that

$z_{y,t,x}\left(s\right)=a\left(t,s\right)x+b\left(t,s\right)y+c\left(t,s\right),$

as desired. (Note: in the second representation of $z_{y\mathrm{,}t\mathrm{,}x}\left(s\right)$ above we need to restrict t to positive values for which $\sin \left(\kappa t\right)\ne 0$ , but this is not a problem because if $T\mathrm{<mo>\; :\; </mo>}=\pi /\kappa$ , then $\sin \left(\kappa t\right)>0$ for all $t\in \left(\mathrm{0,}T\right)$ .)

So as we now assume that $V\left(x\right)$ satisfies Equation (19), we may apply the preceding lemma to infer that there are functions $a\left(t,s\right)$ , $b\left(t,s\right)$ , and $c\left(t,s\right)$ such that

$z_{y,t,x}\left(s\right)=a\left(t,s\right)x+b\left(t,s\right)y+c\left(t,s\right)$ (21)

and

$v_y\left(t\mathrm{,}x\right)=\frac{\partial a}{\partial s}\left(t\mathrm{,}t\right)x+\frac{\partial b}{\partial s}\left(t\mathrm{,}t\right)y+\frac{\partial c}{\partial s}\left(t\mathrm{,}t\right)\mathrm{.}$

Thus

$\text{div}{v}_y\left(t\mathrm{,}x\right)=\frac{\partial v_y}{\partial x}\left(t\mathrm{,}x\right)=\frac{\partial a}{\partial s}\left(t\mathrm{,}t\right)=\mathrm{<mo>\; :\; </mo>}p\left(t\right)\mathrm{,}$

and therefore, Equation (12) assumes the following form:

$v_y\left[{\psi }_y\right]=-p\left(t\right)+iL\left(x\mathrm{,}{v}_y\left(t\mathrm{,}x\right)\right){\psi }_y,$ (22)

where

$L\left(z\mathrm{,}v\right)=\frac{m{v}^2}{2}-V\left(z\right)\mathrm{.}$ (23)

(Note: it is crucial for what follows that $\text{div}{v}_y\left(t\mathrm{,}x\right)$ depends only on t, and hence the restriction to harmonic-oscillator type potentials is crucial as well). To proceed, we observe that

$\begin{array}{c}\frac{\text{d}}{\text{d}s}{\psi }_y\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)={c^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\left[{\psi }_y\right]=v_y\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)\left[{\psi }_y\right]\\ =\left(-p\left(s\right)+iL\left(z_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\mathrm{,}{z^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)\right){\psi }_y\left(c_{y\mathrm{.}t\mathrm{,}x}\left(s\right)\right)\mathrm{,}\end{array}$

and in denoting by P an arbitrary antiderivative of p, we may hence infer that one possible solution of this equation is

${\psi }_y\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)={\text{e}}^{-P\left(s\right)+i{\displaystyle {\int }_0^s}L\left(z_{y\mathrm{,}t\mathrm{,}x}\left(\tau \right)\mathrm{,}{z^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(\tau \right)\right)\text{d}\tau }\mathrm{.}$

Setting $s=t$ yields

${\psi }_y\left(t\mathrm{,}x\right)={\text{e}}^{-P\left(t\right)+i{\displaystyle {\int }_0^t}L\left(z_{y\mathrm{,}t\mathrm{,}x}\left(\tau \right)\mathrm{,}{z^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(\tau \right)\right)\text{d}\tau }\mathrm{,}$

for all $\left(y\mathrm{,}t\mathrm{,}x\right)\in ℝ\times \left(\mathrm{0,}T\right)\times ℝ$ . In order to define a superposition of the functions ${\psi }_y$ analogous to (14), we use (21) and set

$w_y\left(t,x\right):={z^{\prime }}_{y,t,x}\left(0\right)=\frac{\partial a}{\partial s}\left(t,0\right)x+\frac{\partial b}{\partial s}\left(t,0\right)y+\frac{\partial c}{\partial s}\left(t,0\right).$ (24)

Given this definition, it follows that $w_y$ is constant along the flow line described by $c_{y\mathrm{,}t\mathrm{,}x}$ because

$w_y\left(c_{y,t,x}\left(s\right)\right)={z^{\prime }}_{y,c_{y,t,x}\left(s\right)}\left(0\right)={z^{\prime }}_{y,t,x}\left(0\right)=w_y\left(t,x\right).$

(Note: the constancy of $w_y$ along each flow line is obvious also because $w_y\left(x\mathrm{,}t\right)$ is simply the initial velocity of the flow line that starts at $\left(\mathrm{0,}y\right)$ and passes through $\left(t\mathrm{,}x\right)$ ) Consequently, for all $\left(y\mathrm{,}t\mathrm{,}x\right)\in ℝ\times \left(\mathrm{0,}T\right)\times ℝ$ it is the case that

$v_y\left(t\mathrm{,}x\right)\left[w_y\right]={c^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(t\right)\left[w_y\right]={\frac{\text{d}}{\text{d}s}{w}_y\left(c_{y\mathrm{,}t\mathrm{,}x}\left(s\right)\right)|}_{s=t}=\mathrm{0,}$ (25)

and therefore, if $h\left(y\mathrm{,}w\right)$ is differentiable, then

$h\left(y\mathrm{,}{w}_y\left(t\mathrm{,}x\right)\right){\psi }_y\left(t\mathrm{,}x\right)$

is a solution of (22). Hence we may conjecture the general solution of the general Schrödinger Equation (with V given in (19)) to be

$\begin{array}{c}\psi \left(x\mathrm{,}t\right)={\displaystyle {\int }_{-\infty }^{\infty }}h\left(y\mathrm{,}{w}_y\left(t\mathrm{,}x\right)\right){\psi }_y\left(t\mathrm{,}x\right)\text{d}y\\ ={\text{e}}^{-P\left(t\right)}{\displaystyle {\int }_{-\infty }^{\infty }}h\left(y\mathrm{,}{w}_y\left(t\mathrm{,}x\right)\right){\text{e}}^{i{\displaystyle {\int }_0^t}L\left(z_{y\mathrm{,}t\mathrm{,}x}\left(\tau \right)\mathrm{,}{z^{\prime }}_{y\mathrm{,}t\mathrm{,}x}\left(\tau \right)\right)\text{d}\tau }\text{d}y\mathrm{.}\end{array}$

In order to determine h from this suggested equation, we use (24) to introduce the substitution

$\begin{array}{c}y\left(w,t,x\right)=y=\frac{w}{\partial b/\partial s\left(t,0\right)}-\frac{\partial a/\partial s\left(t,0\right)x}{\partial b/\partial s\left(t,0\right)}-\frac{\partial c/\partial s\left(t,0\right)}{\partial b/\partial s\left(t,0\right)}\\ =:\lambda \left(t\right)w+\mu \left(t\right)x+\nu \left(t\right).\end{array}$

(Note: the possibility of expressing y in this way as an affine function of w and x—in direct analogy to the substitution equation $y=x-vt$ or $y=x-wt$ that we used in the free-particle case—is another important reason for assuming that V is an harmonic-oscillator-type potential.) This yields

$\text{d}y=\lambda \left(t\right)\text{d}w\mathrm{,}$

and therefore,

$\psi \left(t\mathrm{,}x\right)=\lambda \left(t\right){\text{e}}^{-P\left(t\right)}{\displaystyle {\int }_{\mp \infty }^{\pm \infty }}h\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}w\right){\text{e}}^{i{\displaystyle {\int }_0^t}{L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}\tau }\text{d}w\mathrm{.}$

Setting

$f\left(t\right)\mathrm{<mo>\; :\; </mo>}=\lambda \left(t\right){\text{e}}^{-P(\; t\; )}$

and taking the derivative with respect to t, we find (in leaving out the argument of h) that

$\begin{array}{c}\frac{\partial \psi }{\partial t}=f^{\prime }\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}h{\text{e}}^{i{\displaystyle {\int }_0^t}{L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}\tau }\text{d}w\\ +f\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}\left({\lambda }^{\prime }\left(t\right)w+{\mu }^{\prime }\left(t\right)x+{\nu }^{\prime }\left(t\right)\right)\frac{\partial h}{\partial y}{\text{e}}^{i{\displaystyle {\int }_0^t}{L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}\tau }\text{d}w\\ +if\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}hL\left(x\mathrm{,}{v}_{y\left(w\mathrm{,}t\mathrm{,}x\right)}\left(t\mathrm{,}x\right)\right){\text{e}}^{i{\displaystyle {\int }_0^t}{L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}\tau }\text{d}w\\ +if\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}h{\displaystyle {\int }_0^t}{\frac{\partial }{\partial t}L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)\text{d}\tau {\text{e}}^{i{\displaystyle {\int }_0^t}L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)\text{d}\tau }|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}w\mathrm{.}\end{array}$

(Note: the plus-or-minus signs in the boundaries indicate that the substitution of w for y changes the boundaries’ signs whenever $\lambda \left(t\right)$ is negative. Intuitively, it is quite easy to see that $\lambda \left(t\right)$ must indeed be negative but a formal confirmation of this fact will only be given in the special case— $\alpha >0$ —that we will discuss at the end of this section) Using the Lagrangian equation of motion

$\frac{\text{d}}{\text{d}\tau }\frac{\partial L}{\partial v}=\frac{\partial L}{\partial z}$

in conjunction with (23), we further observe that

$\begin{array}{l}{\displaystyle {\int }_0^t}{\frac{\partial }{\partial t}L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}\tau \\ ={\displaystyle {\int }_0^t}\left({\frac{\partial L}{\partial z}\frac{\partial z}{\partial t}\left(\tau \right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}+{\frac{\partial L}{\partial v}\frac{\partial z^{\prime }}{\partial t}\left(\tau \right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\right)\text{d}\tau \\ ={\displaystyle {\int }_0^t}\left({\left(\frac{\text{d}}{\text{d}\tau }\frac{\partial L}{\partial v}\right)\frac{\partial z}{\partial t}\left(\tau \right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}+{\frac{\partial L}{\partial v}\left(\frac{\text{d}}{\text{d}\tau }\frac{\partial z}{\partial t}\right)\left(\tau \right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\right)\text{d}\tau \\ ={\displaystyle {\int }_0^t}\left({\frac{\text{d}}{\text{d}\tau }\left(\frac{\partial L}{\partial v}\frac{\partial z}{\partial t}\right)\left(\tau \right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\right)\text{d}\tau \\ =m{z^{\prime }}_{y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x}\left(\tau \right){\frac{\partial z_{y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x}\left(\tau \right)}{\partial t}|}_0^t\end{array}$

$\begin{array}{l}=m{z^{\prime }}_{y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x}\left(\tau \right){\left(\frac{\partial z}{\partial y}\left(\tau \right)\frac{\partial y\left(w,t,x\right)}{\partial t}+\frac{\partial z}{\partial t}\left(\tau \right)\right)|}_0^t\\ =m{v}_{y\left(w,t,x\right)}\left(t,x\right)\left(\frac{\partial x}{\partial y}\frac{\partial y\left(w,t,x\right)}{\partial t}+\left({\frac{\partial z_{y,t,x}\left(\tau \right)}{\partial t}|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\right)\right)\\ -mw\left({\frac{\partial y}{\partial y}|}_{y=y\left(w,t,x\right)}\frac{\partial y\left(w,t,x\right)}{\partial t}+{\frac{\partial y}{\partial t}|}_{y=y\left(w,t,x\right)}\right)\\ =m{v}_{y\left(w,t,x\right)}\left(t,x\right)\left({\frac{\partial z_{y,t,x}\left(\tau \right)}{\partial t}|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\right)-mw\left({\lambda }^{\prime }\left(t\right)w+{\mu }^{\prime }\left(t\right)x+{\nu }^{\prime }\left(t\right)\right).\end{array}$

In order to simplify this resulting expression, we notice, as in (17), that

$z_{y\mathrm{,}t\mathrm{,}x}\left(\tau \right)=z_{y\mathrm{,}{c}_{y\mathrm{,}t\mathrm{,}x}\left(s\right)}(\; \tau \; )$

and that, by implication,

$\begin{array}{c}0={\frac{\text{d}}{\text{d}s}|}_{\left(s,\tau \right)=\left(t,t\right)}{z}_{y,c_{y,t,x}\left(s\right)}\left(\tau \right)={v_y\left(t,x\right)\left[z_{y,t,x}\left(\tau \right)\right]|}_{\tau =t}\\ ={\frac{\partial z_{y,t,x}\left(\tau \right)}{\partial t}|}_{\tau =t}+v_y\left(t,x\right)\frac{\partial z_{y,t,x}\left(t\right)}{\partial x}={\frac{\partial z_{y,t,x}\left(\tau \right)}{\partial t}|}_{\tau =t}+v_y\left(t,x\right)\frac{\partial x}{\partial x}\\ ={\frac{\partial z_{y\mathrm{,}t\mathrm{,}x}\left(\tau \right)}{\partial t}|}_{\tau =t}+v_y\left(t\mathrm{,}x\right)\mathrm{.}\end{array}$

This yields

$\begin{array}{l}{\displaystyle {\int }_0^t}{\frac{\partial }{\partial t}L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}\tau \\ =-m{v}_{y\left(w\mathrm{,}t\mathrm{,}x\right)}{\left(t\mathrm{,}x\right)}^2-mw\left({\lambda }^{\prime }\left(t\right)w+{\mu }^{\prime }\left(t\right)x+{\nu }^{\prime }\left(t\right)\right)\mathrm{,}\end{array}$

and therefore,

$\begin{array}{c}i\frac{\partial \psi }{\partial t}=i{f}^{\prime }\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }h{\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w}\\ +f\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }\left({\lambda }^{\prime }\left(t\right)w+{\mu }^{\prime }\left(t\right)x+{\nu }^{\prime }\left(t\right)\right)\left(i\frac{\partial h}{\partial y}+mwh\right){\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w}\\ +f\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }h}\left(\frac{m{v}_{y\left(w,t,x\right)}{\left(t,x\right)}^2}{2}+V\left(x\right)\right){\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w.\end{array}$ (26)

Similarly, we find that

$\begin{array}{c}\frac{\partial \psi }{\partial x}=f\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}\mu \left(t\right)\frac{\partial h}{\partial y}{\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w\\ +if\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}h{\displaystyle {\int }_0^t}{\frac{\partial }{\partial x}L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}\tau {\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w\end{array}$

and

$\begin{array}{l}{\displaystyle {\int }_0^t{\frac{\partial }{\partial x}L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}}\text{d}\tau \\ ={\displaystyle {\int }_0^t\left({\frac{\text{d}}{\text{d}\tau }\left(\frac{\partial L}{\partial v}\frac{\partial z}{\partial x}\right)\left(\tau \right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\right)\text{d}\tau }\\ =m{z^{\prime }}_{y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x}\left(\tau \right){\left(\frac{\partial z}{\partial y}\left(\tau \right)\frac{\partial y\left(w,t,x\right)}{\partial x}+\frac{\partial z}{\partial x}\left(\tau \right)\right)|}_0^t\\ =m{v}_{y\left(w,t,x\right)}\left(t,x\right)\left(\frac{\partial x}{\partial y}\frac{\partial y\left(w,t,x\right)}{\partial x}+\frac{\partial x}{\partial x}\right)\\ -mw\left({\frac{\partial y}{\partial y}|}_{y=y\left(w,t,x\right)}\frac{\partial y\left(w,t,x\right)}{\partial x}+{\frac{\partial y}{\partial x}|}_{y=y\left(w,t,x\right)}\right)\\ =m{v}_{y\left(w,t,x\right)}\left(t,x\right)-mw\mu \left(t\right).\end{array}$

Thus

$\begin{array}{c}\frac{\partial \psi }{\partial x}=f\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}\mu \left(t\right)\frac{\partial h}{\partial y}{\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w\\ +if\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}mh\left(v_{y\left(w\mathrm{,}t\mathrm{,}x\right)}\left(t\mathrm{,}x\right)-w\mu \left(t\right)\right){\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w\end{array}$

and

$\begin{array}{c}\frac{1}{2m}\frac{{\partial }^2\psi }{\partial x^2}=\frac{f\left(t\right)}{2m}{\displaystyle {\int }_{\mp \infty }^{\pm \infty }}\mu {\left(t\right)}^2\frac{{\partial }^{2}h}{\partial y^2}{\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w\\ +if\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}\mu \left(t\right)\frac{\partial h}{\partial y}\left(v_{y\left(w\mathrm{,}t\mathrm{,}x\right)}\left(t\mathrm{,}x\right)-w\mu \left(t\right)\right){\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w\\ -f\left(t\right){\displaystyle {\int }_{\mp \infty }^{\pm \infty }}\frac{m}{2}h{\left(v_{y\left(w\mathrm{,}t\mathrm{,}x\right)}\left(t\mathrm{,}x\right)-w\mu \left(t\right)\right)}^2{\text{e}}^{i{\displaystyle {\int }_0^{t}L\text{d}\tau }}\text{d}w\mathrm{.}\end{array}$

Finally, in combining this equation with (26), we may infer that

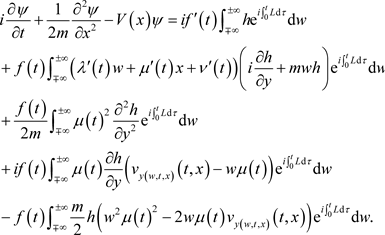
Consequently, $\psi \left(t\mathrm{,}x\right)$ is a solution of the general Schrödinger Equation (with a harmonic-oscillator type potential) if $q_w\left(y\right)\mathrm{<mo>\; :\; </mo>}=h\left(y\mathrm{,}w\right)$ is a solution of the following differential equation:

$\begin{array}{c}0=\frac{f\left(t\right)\mu \left(t\right)}{2m}{q}^{″}\left(y\right)+if\left(t\right)\left({\lambda }^{\prime }\left(t\right)w+{\mu }^{\prime }\left(t\right)x+{\nu }^{\prime }\left(t\right)\right)q^{\prime }\left(t\right)\\ +if\left(t\right)\mu \left(t\right)\left(v_{y\left(w,t,x\right)}\left(t,x\right)-w\mu \left(t\right)\right)q^{\prime }\left(t\right)\\ +i{f}^{\prime }\left(t\right)q\left(t\right)+f\left(t\right)mw\left({\lambda }^{\prime }\left(t\right)w+{\mu }^{\prime }\left(t\right)x+{\nu }^{\prime }\left(t\right)\right)q\left(t\right)\\ -\frac{m}{2}f\left(t\right)\left(w^2\mu {\left(t\right)}^2-2w\mu \left(t\right)v_{y\left(w,t,x\right)}\left(t,x\right)\right)q\left(t\right)\end{array}$ (27)

This equation can easily be solved in general by finding the roots of the corresponding characteristic polynomial, but more natural and instructive is here to consider a concrete example: if $V\left(x\right)=\alpha x^2$ is a genuine harmonic oscillator potential (with $\alpha >0$ and $\beta =\gamma =0$ ), then, according to the proof of Lemma 4.1, it is the case that

$z_{y,t,x}\left(s\right)=\frac{\sin \left(\kappa s\right)x}{\sin \left(\kappa t\right)}+\frac{\sin \left(\kappa \left(t-s\right)\right)y}{\sin (\; \kappa \; t\; )}$

and, by implication,

${z^{\prime }}_{y,t,x}\left(s\right)=\frac{\kappa \cos \left(\kappa s\right)x}{\sin \left(\kappa t\right)}-\frac{\kappa \cos \left(\kappa \left(t-s\right)\right)y}{\sin \left(\kappa t\right)},$

$v_y\left(t,x\right)={z^{\prime }}_{y,t,x}\left(t\right)=\kappa \cot \left(\kappa t\right)x-\frac{\kappa y}{\sin \left(\kappa t\right)},$

$p\left(t\right)=\kappa \cot \left(\kappa t\right)=\text{div}{v}_y\left(t,x\right),$

${\text{e}}^{-P\left(t\right)}=\frac{1}{\sin \left(\kappa t\right)},$

$w_y\left(t,x\right)={z^{\prime }}_{y,t,x}\left(0\right)=\frac{\kappa x}{\sin \left(\kappa t\right)}-\kappa \cot \left(\kappa t\right)y,$

$y\left(w,t,x\right)=-\frac{1}{\kappa }\tan \left(\kappa t\right)w+\frac{x}{\cos \left(\kappa t\right)},$

$\lambda \left(t\right)=-\frac{1}{\kappa }\tan \left(\kappa t\right),$

$\mu \left(t\right)=\frac{1}{\cos \left(\kappa t\right)},$

$\nu \left(t\right)=0,$

$f\left(t\right)=\lambda \left(t\right){\text{e}}^{-P\left(t\right)}=-\frac{1}{\kappa \cos \left(\kappa t\right)},$

$v_{y\left(w,t,x\right)}\left(t,x\right)=\frac{w}{\cos \left(\kappa t\right)}-\kappa \tan \left(\kappa t\right)x$

for all $\left(w\mathrm{,}y\mathrm{,}t\mathrm{,}x\right)\in ℝ\times ℝ\times \left(\mathrm{0,}T\right)\times ℝ$ with $T\mathrm{<mo>\; :\; </mo>}=\pi /\left(2\kappa \right)$ . (Note: T is here reduced from $\pi /\kappa$ in the proof of Lemma 4.1 to $\pi /\left(2\kappa \right)$ because we need to make sure that not only $sin\left(\kappa t\right)$ but also $cos\left(\kappa t\right)$ is different from zero for all $t\in \left(\mathrm{0,}T\right)$ .) Substituting in (27) yields

$q^{″}-\frac{2mwi}{cos\left(\kappa t\right)}{q}^{\prime }+\left(2m\kappa isin\left(\kappa t\right)-\frac{m^2{w}^2}{cos\left(\kappa t\right)}\right)q=0$

and the roots of the corresponding characteristic polynomial are

$\frac{i\left(mw\pm \sqrt{m^2{w}^2\left(1-\cos \left(\kappa t\right)\right)+2m\kappa i\sin \left(\kappa t\right){\cos }^2\left(\kappa t\right)}\right)}{\cos \left(\kappa t\right)}\mathrm{.}$

Consequently, in setting

$h\left(y\mathrm{,}w\right)\mathrm{<mo>\; :\; </mo>}=C\left(w\right){\text{e}}^{iy\left(mw+\sqrt{m^2{w}^2\left(1-\cos \left(\kappa t\right)\right)+2m\kappa i\sin \left(\kappa t\right){\cos }^2\left(\kappa t\right)}\right)/\cos \left(\kappa t\right)}\mathrm{,}$

it follows that

$\boxed{\psi \left(t\mathrm{,}x\right)=\frac{1}{\kappa \cos \left(\kappa t\right)}{\displaystyle {\int }_{-\infty }^{\infty }}h\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}w\right){\text{e}}^{i{\displaystyle {\int }_0^t}{L\left(z\left(\tau \right)\mathrm{,}{z}^{\prime }\left(\tau \right)\right)|}_{\left(y\left(w\mathrm{,}t\mathrm{,}x\right)\mathrm{,}t\mathrm{,}x\right)}\text{d}\tau }\text{d}w}$

with

$y\left(w\mathrm{,}t\mathrm{,}x\right)=-\frac{1}{\kappa }\tan \left(\kappa t\right)w+\frac{x}{\cos (\; \kappa \; t\; )}$

is a solution of the Schrödinger equation in the case where $V\left(x\right)=\alpha x^2$ and $\alpha >0$ . Moreover, the initial condition

$\psi \left(\mathrm{0,}x\right)=\frac{1}{\kappa }{\displaystyle {\int }_{-\infty }^{\infty }}C\left(w\right){\text{e}}^{imwx}\text{d}w$

can once again be easily satisfied by Fourier inversion.

5. The Classical Wave Equation

In order to solve the classical wave equation

$\boxed{\frac{{\partial }^2\psi }{\partial t^2}-v^2\Delta \psi =0}$ (28)

in two spatial dimensions for some given velocity value $v\in \left(\mathrm{0,}\infty \right)$ , we consider, for a given point $\left(x\mathrm{,}y\right)\in {ℝ}^2$ , the positive-time velocity cone

$C_{x\mathrm{,}y}=\left\{\left(t\mathrm{,}x+vtcos\left(\theta \right)\mathrm{,}y+vtsin\left(\theta \right)\right)\in {ℝ}^3|t\ge 0\wedge \theta \in \left[\mathrm{0,2}\pi \right)\right\}\mathrm{.}$

Using the parameterization

$p_{x\mathrm{,}y}\left(t\mathrm{,}\theta \right)=\left(\begin{array}{c}t\\ x+vtcos\left(\theta \right)\\ y+vtsin\left(\theta \right)\end{array}\right)\mathrm{,}$

we find the metric tensor on $C_{x\mathrm{,}y}$ to be

$G=\left(\begin{array}{cc}\frac{\partial p}{\partial t}\cdot \frac{\partial p}{\partial t}& \frac{\partial p}{\partial t}\cdot \frac{\partial p}{\partial \theta }\\ \frac{\partial p}{\partial \theta }\cdot \frac{\partial p}{\partial t}& \frac{\partial p}{\partial \theta }\cdot \frac{\partial p}{\partial \theta }\end{array}\right)=\left(\begin{array}{cc}1+v^2& 0\\ 0& v^2{t}^2\end{array}\right)$

(where the dots represent the ordinary Euclidean inner product in ${ℝ}^3$ ), and the determinant of $G$ is

$g=\left(1+v^2\right)v^2{t}^2\mathrm{.}$

Furthermore, in defining the tangential velocity field

$v_{x\mathrm{,}y}\left(t\mathrm{,}\theta \right)\mathrm{<mo>\; :\; </mo>}=\left(\begin{array}{c}1\\ vcos\left(\theta \right)\\ vsin\left(\theta \right)\end{array}\right)=v^t\frac{\partial p}{\partial t}+v^{\theta }\frac{\partial p}{\partial \theta }=1\frac{\partial p}{\partial t}+0\frac{\partial p}{\partial \theta }=\frac{\partial p}{\partial t}$

on $C_{x\mathrm{,}y}$ , we may use the familiar formula for the divergence of a vector field on a Riemannian manifold to infer that

$\text{div}{v}_{x,y}\left(t,\theta \right)=\frac{1}{\sqrt{g}}\left(\frac{\partial }{\partial t}\left(\sqrt{g}{v}^t\right)+\frac{\partial }{\partial \theta }\left(\sqrt{g}{v}^{\theta }\right)\right)=\frac{\partial \left(\sqrt{1+v^2}vt\right)/\partial t}{\sqrt{1+v^2}vt}=\frac{1}{t}.$ (29)

Consequently, as we now consider a free particle of mass m that moves along the trajectory on $C_{x\mathrm{,}y}$ that is described by the equation

$c_{x\mathrm{,}y\mathrm{,}\theta }\left(t\right)\mathrm{<mo>\; :\; </mo>}=p_{x\mathrm{,}y}\left(t\mathrm{,}\theta \right)$

for any fixed value $\theta \in \left[\mathrm{0,2}\pi \right)$ , we may infer that the Lagrangian is $m{v}^2/2$ and that therefore Equation (12) assumes the following form:

$v_{x,y}\left[{\psi }_{x,y,m}^{\pm }\right]=\left(-\frac{1}{t}\pm \frac{im{v}^2}{2}\right){\psi }_{x,y,m}^{\pm }.$ (30)

Thus

$\frac{\text{d}}{\text{d}s}{\psi }_{x,y}^{\pm }\left(c_{x,y,\theta }\left(s\right)\right)=\left(-\frac{1}{s}\pm \frac{im{v}^2}{2}\right){\psi }_{x,y,m}^{\pm }\left(c_{x,y,\theta }(\; s\; )\right)$

and one possible solution of this equation is

${\psi }_{x,y,m}^{\pm }\left(c_{x,y,\theta }\left(s\right)\right)=\frac{{\text{e}}^{\pm im{v}^{2}s/2}}{2\pi vs}.$

Setting $s=t$ , we find that

${\psi }_{x,y,m}^{\pm }\left(t,\theta \right):={\psi }_{x,y,m}^{\pm }\left(c_{x,y,\theta }\left(t\right)\right)=\frac{{\text{e}}^{\pm im{v}^{2}t/2}}{2\pi vt},$ (31)

where the factor $2\pi v$ in the denominator is inserted in order to guarantee that the integral of ${\psi }_{x\mathrm{,}y\mathrm{,}m}^{\pm }$ along each cross-sectional circle

$\left\{c_{x\mathrm{,}y\mathrm{,}\theta }\left(t\right)\in C_{x\mathrm{,}y}|\theta \in \left[\mathrm{0,2}\pi \right)\right\}$

is equal to one. That said, we move on to construct the general solution $\psi$ of the classical wave equation by superimposing functions of the form

$h^{\pm }\left(x\mathrm{,}y\mathrm{,}m\mathrm{,}\theta \right){\psi }_{x\mathrm{,}y\mathrm{,}m}^{\pm }\left(t\mathrm{,}\theta \right)=h^{\pm }\left(x\mathrm{,}y\mathrm{,}m\mathrm{,}\theta \right)\frac{{\text{e}}^{\pm im{v}^{2}t/2}}{2\pi vt}$

as m ranges from 0 to $\infty$ and as $\left(x\mathrm{,}y\right)$ traces out circles of radius vt in the xy-plane. This yields

$\begin{array}{c}\psi \left(t\mathrm{,}x\mathrm{,}y\right)={\displaystyle {\int }_0^{\infty }}{\displaystyle {\int }_0^{2\pi }}{h}^{+}\left(x-vt\cos \left(\theta \right),y-vt\sin \left(\theta \right),m,\theta \right)\frac{{\text{e}}^{im{v}^{2}t/2}}{2\pi vt}vt\text{d}\theta \text{d}m\\ +{\displaystyle {\int }_0^{\infty }}{\displaystyle {\int }_0^{2\pi }}{h}^{-}\left(x-vt\cos \left(\theta \right),y-vt\sin \left(\theta \right),m,\theta \right)\frac{{\text{e}}^{-im{v}^{2}t/2}}{2\pi vt}vt\text{d}\theta \text{d}m,\end{array}$ (32)

where the factor vt at the end of each integrand is accounted for by the fact that

$vt=\Vert \frac{\text{d}}{\text{d}\theta }\left(\begin{array}{c}0\\ x-vtcos\left(\theta \right)\\ y-vtsin\left(\theta \right)\end{array}\right)\Vert \mathrm{.}$

To proceed, we take the second partial derivatives of $\psi$ with respect to t, x and y:

and

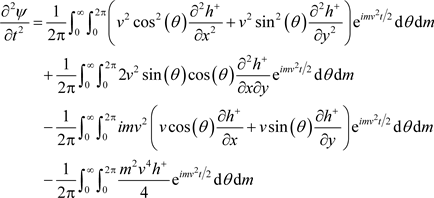
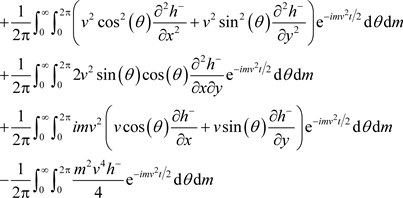
and

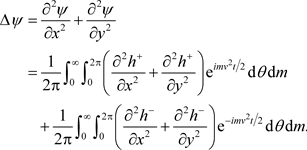
Thus

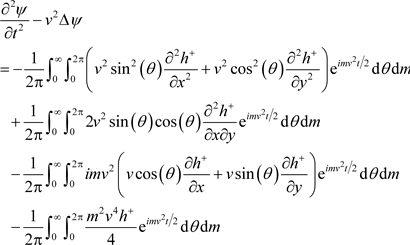
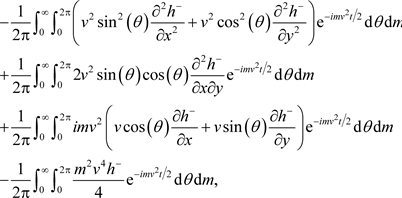
and in setting $z_{m\mathrm{,}\theta }^{\pm }\left(x\mathrm{,}y\right)\mathrm{<mo>\; :\; </mo>}=h^{\pm }\left(x\mathrm{,}y\mathrm{,}m\mathrm{,}\theta \right)$ we may infer that $\psi$ , as defined in (32), is a solution of the classical wave equation if $z_{m\mathrm{,}\theta }^{\pm }$ satisfies the partial differential equation

$\begin{array}{l}0=-v^2{\sin }^2\left(\theta \right)\frac{{\partial }^{2}z}{\partial x^2}-v^2{\cos }^2\left(\theta \right)\frac{{\partial }^{2}z}{\partial y^2}+2v^2\sin \left(\theta \right)\cos \left(\theta \right)\frac{{\partial }^{2}z}{\partial x\partial y}\\ \mp im{v}^2\left(v\cos \left(\theta \right)\frac{\partial z}{\partial x}+v\sin \left(\theta \right)\frac{\partial z}{\partial y}\right)-\frac{m^2{v}^{4}z}{4}.\end{array}$ (33)

In substituting for $z_{m\mathrm{,}\theta }^{\pm }\left(x\mathrm{,}y\right)$ a function of the form $C^{\pm }\left(m\mathrm{,}\theta \right){\text{e}}^{ax+by}$ , it follows that the characteristic polynomial of the differential equation above is

$\begin{array}{c}{P}^{\pm }\left(a\mathrm{,}b\right)=-v^{2}si{n}^2\left(\theta \right)a^2-v^{2}co{s}^2\left(\theta \right)b^2+2v^{2}sin\left(\theta \right)cos\left(\theta \right)ab\\ \mp im{v}^2\left(vcos\left(\theta \right)a+vsin\left(\theta \right)b\right)-\frac{m^2{v}^{4}z}{4}.\end{array}$

In order to eliminate the mixed term $2v^{2}sin\left(\theta \right)cos\left(\theta \right)ab$ , we introduce the substitutions

$a=cos\left(\theta \right)\alpha -sin\left(\theta \right)\beta \mathrm{,}$

$b=sin\left(\theta \right)\alpha +cos\left(\theta \right)\beta \mathrm{.}$

In doing so, the equation $0=P^{\pm }\left(a\mathrm{,}b\right)$ is easily seen to be turned into the equation

$0={\beta }^2\pm imv\alpha +\frac{m^2{v}^2}{4}.$

Choosing $\alpha =0$ and $\beta =imv/2$ , we may infer that the function

$\begin{array}{c}{z}_{m,\theta }^{\pm }\left(x,y\right)=C^{\pm }\left(m,\theta \right){\text{e}}^{ax+by}=C^{\pm }\left(m,\theta \right){\text{e}}^{\left(\cos \left(\theta \right)\alpha -\sin \left(\theta \right)\beta \right)x+\left(\sin \left(\theta \right)\alpha +\cos \left(\theta \right)\beta \right)y}\\ =C^{\pm }\left(m,\theta \right){\text{e}}^{imv\left(-\sin \left(\theta \right)x+\cos \left(\theta \right)y\right)/2}\end{array}$

is a solution of (33). Consequently, as we substitute $x-vtcos\left(\theta \right)$ for x and $y-vtsin\left(\theta \right)$ for y (see (32)), we find that

$\begin{array}{c}\psi \left(t\mathrm{,}x\mathrm{,}y\right)=\frac{1}{2\pi }{\displaystyle {\int }_0^{\infty }}{\displaystyle {\int }_0^{2\pi }}{C}^{+}\left(m\mathrm{,}\theta \right){\text{e}}^{imv\left(-sin\left(\theta \right)x+cos\left(\theta \right)y+vt\right)/2}\text{d}\theta \text{d}m\\ +\frac{1}{2\pi }{\displaystyle {\int }_0^{\infty }}{\displaystyle {\int }_0^{2\pi }}{C}^{-}\left(m\mathrm{,}\theta \right){\text{e}}^{imv\left(-sin\left(\theta \right)x+cos\left(\theta \right)y-vt\right)/2}\text{d}\theta \text{d}m\end{array}$

is a solution of the classical wave equation. In order to represent this solution in a form that allows us to use Fourier inversion to match given initial conditions, we introduce the polar substitution

$\left(\begin{array}{c}p\\ q\end{array}\right)=\left(\begin{array}{c}-mv\sin \left(\theta \right)/2\\ mv\cos \left(\theta \right)/2\end{array}\right).$

Given this substitution, it follows that $mv/2=\sqrt{p^2+q^2}$ , and therefore, there exist coefficient functions $B^{\pm }\left(p\mathrm{,}q\right)$ such that

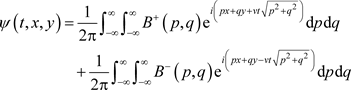
Hence

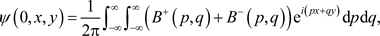
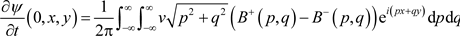(34)

and therefore,

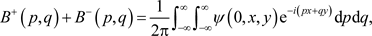
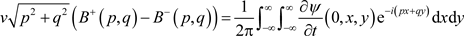
by Fourier inversion. Finally, in solving these two equations for $B^{+}$ and $B^{-}$ , the desired solution of the initial value problem (34) is obtained.

6. The Electromagnetic Wave Equation

The problem of solving the electromagnetic wave equation

$\begin{array}{c}\frac{{\partial }^2\psi }{\partial t^2}-\Delta \psi =0\end{array}$ (35)

may seem to be a mere special case of the classical wave equation and therefore redundant, but insofar as the choice $v=1$ that turns (28) into (35) is understood to be a relativistic one, it may be helpful to explain how certain technical difficulties that this choice entails can properly be handled.

In a special relativistic setting the Euclidean inner product that we used to calculate the metric tensor G on the velocity cone $C_{x\mathrm{,}y}$ is naturally replaced by the Lorentz inner product, and thus we find that

$G=\left(\begin{array}{cc}\frac{\partial p}{\partial t}\cdot \frac{\partial p}{\partial t}& \frac{\partial p}{\partial t}\cdot \frac{\partial p}{\partial \theta }\\ \frac{\partial p}{\partial \theta }\cdot \frac{\partial p}{\partial t}& \frac{\partial p}{\partial \theta }\cdot \frac{\partial p}{\partial \theta }\end{array}\right)=\left(\begin{array}{cc}1-v^2& 0\\ 0& -v^2{t}^2\end{array}\right)$

(where the dots represent the Lorentz inner product in ${ℝ}^3$ ), and the determinant of $G$ is

$g=-\left(1-v^2\right)v^2{t}^2\mathrm{.}$

So if $v=1$ (the speed of light) then $g=0$ and the metric induced by $G$ on $C_{x,y}=\left\{\left(t,x+vt\cos \left(\theta \right),y+vt\sin \left(\theta \right)\right)\in {ℝ}^3|t\ge 0\wedge \theta \in \left[0,2\pi \right)\right\}$ becomes degenerate and the divergence of

$v_{x\mathrm{,}y}\left(t\mathrm{,}\theta \right)=\left(\begin{array}{c}1\\ vcos\left(\theta \right)\\ vsin(\; \theta \; )\end{array}\right)$

becomes undefined (according to the formula we used in (29)). However, for values $v\in \left(\mathrm{0,1}\right)$ , the divergence of $v_{x\mathrm{,}y}$ can easily be calculated using essentially the same formula as in (29):

$\text{div}{v}_{x,y}\left(t,\theta \right)=\frac{1}{\sqrt{-g}}\left(\frac{\partial }{\partial t}\left(\sqrt{-g}{v}^t\right)+\frac{\partial }{\partial \theta }\left(\sqrt{-g}{v}^{\theta }\right)\right)=\frac{\partial \left(\sqrt{1-v^2}vt\right)/\partial t}{\sqrt{1-v^2}vt}=\frac{1}{t}.$

Using this result, we may now replace the classical kinetic energy $m{v}^2/2$ by the relativistic kinetic energy $m/\sqrt{1-v^2}$ (relative to an intertial observer whose worldline is the t-axis) and thereby turn Equation (30) into the equation

$v_{x,y}\left[{\psi }_{x,y,m}^{\pm }\right]=\left(-\frac{1}{t}\pm \frac{im}{\sqrt{1-v^2}}\right){\psi }_{x,y,m}^{\pm }.$

Moreover, in order to determine the limiting form of this equation, as v approaches 1 and as m approaches zero (the restmass of a photon), we may naturally assume that the kinetic energy $m/\sqrt{1-v^2}$ approaches a limiting photon-energy value $E=h\nu$ . This yields

$v_{x,y}\left[{\psi }_{x,y,E}^{\pm }\right]=\left(-\frac{1}{t}\pm iE\right){\psi }_{x,y,E}^{\pm }.$ (36)

and the solution corresponding to (31) is

${\psi }_{x\mathrm{,}y\mathrm{,}E}^{\pm }\left(t\mathrm{,}\theta \right)=\frac{{\text{e}}^{\pm iEt}}{2\pi t}\mathrm{.}$

Consequently, in direct analogy to (32), the general solution of the electromagnetic wave equation is

$\begin{array}{c}\psi \left(t,x,y\right)=\frac{1}{2\pi }{\displaystyle {\int }_0^{\infty }}{\displaystyle {\int }_0^{2\pi }}{h}^{+}\left(x-t\cos \left(\theta \right),y-t\sin \left(\theta \right),E,\theta \right){\text{e}}^{iEt}\text{d}\theta \text{d}E\\ +\frac{1}{2\pi }{\displaystyle {\int }_0^{\infty }}{\displaystyle {\int }_0^{2\pi }}{h}^{-}\left(x-t\cos \left(\theta \right),y-t\sin \left(\theta \right),E,\theta \right){\text{e}}^{-iEt}\text{d}\theta \text{d}E,\end{array}$

and the differential equation corresponding to (33) is

$\begin{array}{c}0=-si{n}^2\left(\theta \right)\frac{{\partial }^{2}z}{\partial x^2}-co{s}^2\left(\theta \right)\frac{{\partial }^{2}z}{\partial y^2}+2sin\left(\theta \right)cos\left(\theta \right)\frac{{\partial }^{2}z}{\partial x\partial y}\\ \mp 2iEcos\left(\theta \right)\frac{\partial z}{\partial x}+sin\left(\theta \right)\frac{\partial z}{\partial y}-E^{2}z.\end{array}$

So from this point onward, the process of solving the electromagnetic wave equation is completely parallel to the way in which we solved the classical wave equation in the previous section. In summary therefore we may say that while we were not able represent $\psi$ as a superposition of solutions of an equation of the form

$\text{div}\left({\psi }_{x\mathrm{,}y}{v}_{x\mathrm{,}y}\right)=\pm i{L}_{x\mathrm{,}y}\mathrm{,}$

due to the degeneracy of the Lorentz metric on a light cone, we did manage to represent it as a superposition of solutions of a limiting Equation (namely Equation (36)) that the equation above generates (as v approaches 1).

7. Conclusion

We demonstrated that the complete set of solutions of the Klein-Gordon equation, the Schrödinger Equation (with harmonic-oscillator potential), and the classical wave equation can be constructed by superimposing solutions of the velocity-field divergence Equation (3). In doing so we brought to light an underlying mathematical unity that, in similar fashion, was previously found in [2] to underlie as well the gravitational field equations of Newton and Einstein.

Acknowledgements

I would like to thank my former colleague, the late Gaston Griggs, for many stimulating discussions concerning the nature of time and the structure of modern physical theories.

Conflicts of Interest

The author declares no conflicts of interest regarding the publication of this paper.

References

[1]	Blume, F. (2013) A Derivation of the Path-Integral Formalism of Quantum Mechanics from Probability Conservation along the Velocity Flows of Classical Particles. Quantum Physics Letters, 2, 17-24. https://doi.org/10.12785/qpl/020201
[2]	Blume, F. (2022) On the Transition from Newtonian Gravity to General Relativity. Journal of Applied Mathematics and Physics, 10, 1461-1476. https://doi.org/10.4236/jamp.2022.105103
[3]	James, C. (2000) The Geometry of Spacetime. Springer-Verlag, New York. https://doi.org/10.1007/978-1-4757-6736-0
[4]	Jürgen, E. (1997) Examples of Newtonian Limits of Relativistic Spacetimes. Classical and Quantum Gravity, 14, A119-A126. https://doi.org/10.1088/0264-9381/14/1A/010
[5]	Epstein, B. (1962) Partial Differential Equations. McGraw Hill, New York.
[6]	Fletcher, S.C. (2019) On the Reduction of General Relativity to Newtonian Gravitation. Studies in the History and Philosophy of Modern Physics, 68, 1-15. https://doi.org/10.1016/j.shpsb.2019.04.005
[7]	Flügge, S. (1999) Practical Quantum Mechanics. Springer, Berlin.
[8]	Greenspan, D. (1961) Introduction to Partial Differential Equations. McGraw Hill, New York.
[9]	Misner, C.W., Thorne, K.S. and Wheeler, J.A. (1973) Gravitation. W. H. Freeman and Company, San Francisco.
[10]	Zauderer, E. (1983) Partial Differential Equations of Applied Mathematics. Wiley, New York.