Applied Mathematics
Vol.06 No.05(2015), Article ID:56316,10 pages
10.4236/am.2015.65076
Blow Up and Global Existence for a Nonlinear Viscoelastic Wave Equation with Strong Damping and Nonlinear Damping and Source terms
Liang Guo, Zhaoqin Yuan, Guoguang Lin
Department of Mathematics, Yunnan University, Kunming, China
Email: guoliang142857@163.com, yuanzq091@163.com, gglin@ynu.edu.cn
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 30 March 2015; accepted 12 May 2015; published 14 May 2015
ABSTRACT
In this paper, we consider an initial-boundary value problem for a nonlinear viscoelastic wave equation with strong damping, nonlinear damping and source terms. We proved a blow up result for the solution with negative initial energy if p > m, and a global result for p ≤ m.
Keywords:
Viscoelastic Equation, Blow Up, Global Existence

1. Introduction
A purely elastic material has a capacity to store mechanical energy with no dissipation (of the energy). A complete opposite to an elastic material is a purely viscous material. The important thing about viscous materials is that when the force is removed it does not return to its original shape. Materials which are outside the scope of these two theories will be those for which some, but not all, of the work done to deform them can be recovered. Such materials possess a capacity of storage and dissipation of mechanical energy. This is the case for viscoelastic material. The dynamic properties of viscoelastic materials are of great importance and interest as they appear in many applications to natural sciences. Many authors have given attention to this problem for quite a long time, especially in the last two decades, and have made a lot of progress.
In [1] , Messaoudi considered the following initial-boundary value problem:
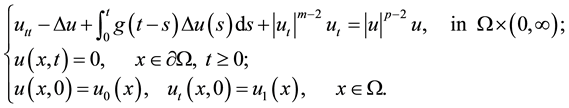 (1.1)
(1.1)
where 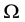 was a bounded domain of
was a bounded domain of 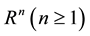 with a smooth boundary
with a smooth boundary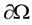 ,
, 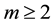 , p > 2, and
, p > 2, and 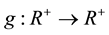 was a positive nonincreasing function. He proved a blow up result for the solution with negative initial energy if
was a positive nonincreasing function. He proved a blow up result for the solution with negative initial energy if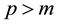 , and a global result for
, and a global result for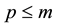 . This result was later improved by Messaoudi [2] , to certain solutions with positive initial energy. A similar result was also obtained by Wu [3] using a different method.
. This result was later improved by Messaoudi [2] , to certain solutions with positive initial energy. A similar result was also obtained by Wu [3] using a different method.
For the problem (1.1) in 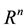 and with
and with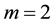 , concerning Cauchy problems, Kafini and Messaoudi [4] established a blow up result for the problem
, concerning Cauchy problems, Kafini and Messaoudi [4] established a blow up result for the problem
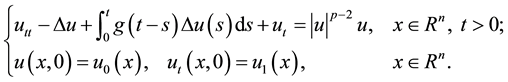 (1.2)
(1.2)
where 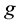 satisfied
satisfied 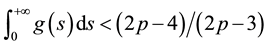 and the initial data were compactly supported with negative
and the initial data were compactly supported with negative
energy such that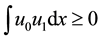 .
.
In the absence of the viscoelastic term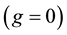 , the problem has been extensively studied and results concerning existence and nonexistence have been established. In bounded domains, for the equation
, the problem has been extensively studied and results concerning existence and nonexistence have been established. In bounded domains, for the equation
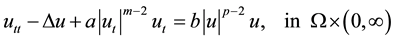 (1.3)
(1.3)







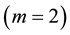

In [11] , Berrimi and Messaoudi considered

in a bounded domain and
In [12] , Song and Xue considered with the following viscoelastic equation with strong damping:

where 






In this work, we intend to study the following initial-boundary value problem:

where 




for the problem (1.6), the memory term 

and we consider the strong damping term 

Now, we shall add a new variable 

A direct computation yields

Thus, the original memory term can be written as

and we get a new system


with the initial conditions

and boundary conditions

The paper is organized as follows. In Section 2, we first prove the blow up result, and then in Section 3, we prove the global existence result.
For convenience, we denote the norm and scalar product in 




2. Blow Up
In this section, we present some materials needed in the proof of our results, state a local existence result, which can be established, combining the argument of [21] , and prove our main result. For this reason, we assume that
(G1) 

(G2)
(G3) There exists a constant 


We start with a local existence theorem which can be established by the Faedo-Galerkin methods. The interested readers are referred to Cavalcanti, Domingos Cavalcanti and Soriano [22] for details:
Theorem 2.1. Assume (G1) holds. Let 

Then for any initial data

with compact support, problem (1.10) has a unique solution
for some
Lemma 2.2. Assume (G1), (G2), (G3) and (2.1) hold. Let 


where

Proof. By multiplying the Equation in (1.10) by 


For the fourth term on the left side (2.4), by using (1.11), (G2) and (G3), we have

where

Then, we obtain

So, we have

where
Our main result reads as follows.
Lemma 2.3. Suppose that (2.1) holds. Then there exists a positive constant 

for any 

Proof. If
So, we obtain
If
Therefore (2.9) follows.
We get

and use, throughout this paper, C to denote a generic positive constant.
As a result of (2.3) and (2.5), we have
Corollary 2.4. Suppose that (2.1) holds. Then, we have

for any 

Lemma 2.5. (

where

Proof. We set
By taking a derivative of
If



Then, we have
If



The proof is completed.
Next, we have the following theorem concerning blow up.
Theorem 2.6. Assume (G1), (G2), (G3) and (2.1) hold. Let


if 

Proof. From (2.2), we have

consequently, we have

Similar to [18] , then we define the weighed functional

where 

By multiplying (1.10) by 

By using Holder inequality and Young’s inequality to estimate the fourth term on the right hand side of (2.19)

for some number 


Then, we have

that is

By using Holder inequality and Young’s inequality to estimate the last two terms on right hand side of (2.24), we obtain

and

and

Substituting (2.24), (2.25) and (2.26) and to (2.23), we have

by taking 



by taking proper



so, we have

From (2.16), we have

Then, hence (2.31) yields

where





Writing



where
From (2.3) and (G1) we have

writing


at this point, we choose 



By using Holder inequality and Young’s inequality, we next estimate

and

which implies

where



By using 

According to (2.36) and (2.41), we get

where

So, we know 

3. Global Existence
In this section, we show that solution of (1.10) is global if
Lemma 3.1. For


Proof.

so, 
Theorem 3.2. Assume (G1), (G2) and (G3) hold. Let 

for any
Proof. Similar to [23] , we set

from (2.3), we have

By differentiating 

By using Holder inequality and Young’s inequality, we next estimate

Setting


Substituting (3.5) to (3.3), we have

so, there exist a small enough constant 

Then, by using Gronwall inequality and continuation principle, we complete the proof of the global existence result.
Acknowledgements
The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper.
This work is supported by the National Natural Sciences Foundation of People’s Republic of China under Grant 11161057
References
- Messaoudi, S.A. (2003) Blow Up and Global Existence in a Nonlinear Viscoelastic Wave Equation. Mathematische Nachrichten, 260, 58-66. http://dx.doi.org/10.1002/mana.200310104
- Messaoudi, S.A. (2006) Blow Up of Positive-Initial-Energy Solutions of a Nonlinear Viscoelastic Hyperbolic Equation. Journal of Mathematical Analysis and Applications, 320, 902-915. http://dx.doi.org/10.1016/j.jmaa.2005.07.022
- Wu, S.T. (2006) Blow-Up of Solutions for an Integro-Differential Equation with a Nonlinear Source. Electronic Journal of Differential Equations, 45, 1-9.
- Kafini, M., Messaoudi, S.A. (2008) A Blow-Up Result in a Cauchy Viscoelastic Problem. Applied Mathematics Letters, 21, 549-553. http://dx.doi.org/10.1016/j.aml.2007.07.004
- Ball, J. (1977) Remarks on Blow-Up and Nonexistence Theorems for Nonlinear Evolutions Equation. Quarterly Journal of Mathematics, 28, 473-486. http://dx.doi.org/10.1093/qmath/28.4.473
- Haraux, A. and Zuazua, E. (1988) Decay Estimates for Some Semilinear Damped Hyperbolic Problems. Archive for Rational Mechanics and Analysis, 100, 191-206. http://dx.doi.org/10.1007/BF00282203
- Levine, H.A. (1974) Instability and Nonexistence of Global Solutions of Nonlinear Wave Equation of the Form Putt = Au + F(u). Transactions of the American Mathematical Society, 192, 1-21.
- Levine, H.A. (1974) Some Additional Remarks on the Nonexistence of Global Solutions to Nonlinear Wave Equation. SIAM Journal on Mathematical Analysis, 5, 138-146. http://dx.doi.org/10.1137/0505015
- Georgiev, V. and Todorova, G. (1994) Existence of Solutions of the Wave Equation with Nonlinear Damping and Source Terms. Journal of Differential Equations, 109, 295-308. http://dx.doi.org/10.1006/jdeq.1994.1051
- Messaoudi, S.A. (2001) Blow Up in a Nonlinearly Damped Wave Equation. Mathematische Nachrichten, 231, 105- 111. http://dx.doi.org/10.1002/1522-2616(200111)231:1<105::AID-MANA105>3.0.CO;2-I
- Berrimi, S. and Messaoudi, S.A. (2006) Existence and Decay of Solutions of a Viscoelastic Equation with a Nonlinear Source. Nonlinear Analysis, 64, 2314-2331. http://dx.doi.org/10.1016/j.na.2005.08.015
- Song, H.T. and Xue, D.S. (2014) Blow up in a Nonlinear Viscoelastic Wave Equation with Strong Damping. Nonlinear Analysis, 109, 245-251. http://dx.doi.org/10.1016/j.na.2014.06.012
- Song, H.T. and Zhong, C.K. (2010) Blow-Up of Solutions of a Nonlinear Viscoelastic Wave Equation. Nonlinear Analysis: Real World Applications, 11, 3877-3883. http://dx.doi.org/10.1016/j.nonrwa.2010.02.015
- Lu, L.Q. and Li, S.J. (2011) Cauchy Problem for a Nonlinear Viscoelastic Equation with Nonlinear Damping and Source Term. Applied Mathematics Letters, 24, 1275-1281. http://dx.doi.org/10.1016/j.aml.2011.01.009
- Kafini, M. and Mustafa, M.I. (2014) Blow-Up Result in a Cauchy Viscoelastic Problem with Strong Damping and Dispersive. Nonlinear Analysis: Real World Applications, 20, 14-20. http://dx.doi.org/10.1016/j.nonrwa.2014.04.005
- Kafini, M. and Messaoudi, S.A. (2008) A Blow-Up Result in a Cauchy Viscoelastic Problem. Applied Mathematics Letters, 21, 549-553. http://dx.doi.org/10.1016/j.aml.2007.07.004
- Cavalcanti, M.M., Domingos Cavalcanti, V.N. and Soriano, J.A. (2002) Exponential Decay for the Solution of Semilinear Viscoelastic Wave Equation with Localized Damping. Electronic Journal of Differential Equations, 2002, 1-14.
- Cavalcanti, M.M., Domingos Cavalcanti, V.N. and Ferreira, J. (2001) Existence and Uniform Decay for Nonlinear Viscoelastic Equation with Strong Damping. Mathematical Methods in the Applied Sciences, 24, 1043-1053. http://dx.doi.org/10.1002/mma.250
- Qin, Y.M., Feng, B.W. and Zhang, M. (2014) Uniform Attractors for a Non-Autonomous Viscoelastic Equation with a Past History. Nonlinear Analysis, 101, 1-15. http://dx.doi.org/10.1016/j.na.2014.01.006
- Conti, M., Marchini, E.M. and Pata, V. (2014) A Well Posedness Result for Nonlinear Viscoelastic Equations with Memory. Nonlinear Analysis, 94, 206-216. http://dx.doi.org/10.1016/j.na.2013.08.015
- Zhou, Y. (2005) A Blow-Up Result for a Nonlinear Wave Equation with Damping and Vanishing Initial Energy in RN. Applied Mathematics Letters, 18, 281-286. http://dx.doi.org/10.1016/j.aml.2003.07.018
- Cavalcanti, M.M., Domingos Cavalcanti, V.N. and Soriano, J.A. (2002) Global Existence and Asymptotic Stability for Viscoelastic Problems. Differential Integral Equations, 15, 731-748.
- Lu, L.Q. and Li, S.J. (2011) Cauchy Problem for a Nonlinear Viscoelastic Equation with Nonlinear Damping and Source Term. Applied Mathematics Letters, 24, 1275-1281. http://dx.doi.org/10.1016/j.aml.2011.01.009













