ABSTRACT

Growth rate of Yarrowia lipolytica NCIM 3589 was observed in a fermentation medium consisting of peptone, yeast extract, sodium chloride. Logistic equation was fitted to the growth data (time vs. biomass concentration) and compared with the prediction given by Artificial Neural Networks (ANN). ANN was found to be superior in describing growth characteristics. A single MATLAB programme is developed to fit the growth data by logistic equation and ANN.

1. INTRODUCTION

Yarrowia lipolytica is one of the most extensively studied ‘‘non-conventional’’ yeasts which is currently used as a model for the study of protein secretion, peroxisome biogenesis, dimorphism, degradation of hydrophobic substrates, and several new fields. Recently, the entire sequence of the six Y. lipolytica chromosomes has been determined [1], allowing its admission into the ‘‘omic’’ disciplines such as genomics, transcriptomics and proteomics. Several reviews have already been published on its physiology and genetics [2-4], secretion [5-7], dimorphism [8], peroxisome biogenesis [9,10] and mitochondrial complex I [11].

Yarrowia lipolytica is ascomycetous yeast which has been assigned to the family Dipodascaceae [12]. This organism is non-pathogenic and oil degrading yeast. It is suitable for the aerobic biodegradation and detoxification of oil mill waste water. It is good for the waste water purification and reduction of pollution due to its ability to reduce chemical oxygen demand and biological oxygen demand. It is also suggested for a deliberate use in cheese ripening due to its extra cellular enzyme activities. It is therefore important to know the growth behavior of this microorganism. The growth capacity of the organism can be evaluated by using growth curves which can be plotted by taking log number of cells versus incubation time. Logistic equation is conveniently used to evaluate the growth capacity of the organism.

Recently, a number of new models have been introduced which involve the application of artificial neural networks to describe the complex growth of yeasts. ANN is highly interconnected network consisting of many simple processing elements capable of performing a massively parallel computation for data processing inspired by the elementary principles of the nervous system. ANN tends to correlate the input data with the output data. In this paper, the growth data were fitted by using both logistic equation and ANN.

2. MATERIALS AND METHODS

2.1. Microorganism

Y. lipolytica NCIM3589 obtained from National Chemical Laboratory, Pune, India, was used throughout the study.

2.2. Growth Conditions

The culture was maintained on MGYP slants having the composition (%): malt extract 0.3, glucose 1.0, yeast extract 0.3, peptone 0.5 and agar agar 2.0. The pH of the medium was adjusted to 6.4–6.8 and culture was incubated at 30^oC for 48 h. Sub-culturing was carried out once in every 2 weeks and the culture was stored at 4^oC.

2.3. Growth of Y. lipolytica

The yeast Yarrowia strain was cultivated in a medium containing peptone 5 g, yeast extract 3 g and sodium chloride 3 g/l of distilled water. The cells were culti

vated in this medium at 30^oC on a shaker at 200 rpm for 24 h [13]. The growth data was taken using double beam spectrophotometer with which optical density was taken at 570 nm. The observations were noted each hour until the organism has reached the stationary stage of growth and the data were reported in Table 1" target="_self"> Table 1.

2.4. Logistic Growth Model

Using the logistic model, the growth curve assumes a sigmoidal shape by plotting biomass vs. time. This shape can be predicted by combining the Monod equation with the growth equation and an equation for the yield of cell mass based on substrate consumption is given by

(1)

The specific growth rate is related to the amount of unused carrying capacity as

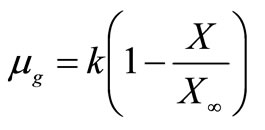(2)

Thus,

(3)

The integration of the equation yields [14]

X =                                                             (4)

where X₀ = initial concentration of biomass, g/l X_∞ = concentration of biomass at infinite time, g/l  

k = rate constant, h-1.

This is the logistic function relating biomass “X” with time “t” with unknown coefficients k and X_∞ which are to be estimated using non-linear least squares. However, non-linear least squares routine requires the initial guess values of k and X_∞. The guess value for X_∞ might be taken as 1.01 times the end value of biomass, while a guess value for k can be calculated by approximating the eq.3 for a pair of data points as follows:

k =

where is the average of two data points, is the difference between the two data points, is the corresponding difference in time. Non-linear regression routine, ‘nlinfit’ of MATLAB 7, was used to estimate the values of k and X_∞. The predicted biomass values were reported in Table 1 as the fourth column.

2.5. Artificial Neural Networks

A neural network is a mathematical representation of the neurological functioning of the brain. It stimulates the brain learning process by mathematical modeling of the network structure of interconnected nerve cells. The essential requirement of neural network modeling was sufficient number of data as it operates directly on inputoutput data. Thus, ANN is purely data driven model made up of inter connected processing elements called neurons that are arranged in layers. The most important of this modeling methodology is its ability to reduce the complexity of the network. A good introduction to the subject with respect to MATLAB usage is given by Demuth et al. [15].

The type of ANN used is the Generalized Regression Neural Networks (GRNN) which is mainly based on non-linear regression theory. ANN approximates any arbitrary function between input and output vectors, drawing function estimate directly from the training data. GRNN has four layers: input, a layer of radial centers, a layer of regression units and output. The radial layer units represent the centers of clusters of known training data. This layer must be trained by a clustering algorithm such as sub sampling. Thus, GRNN is a universal approximator for smooth function, so it should be able to solve any smooth function approximation problem given enough data.

Using MATLAB 7, the biomass values and time data were fitted by GRNN and predicted values were reported in Table 1 as the fifth column.

3. RESULTS AND DISCUSSION

The experimental growth data was fitted by using both logistic equation and ANN. In logistic growth model, the parameter values (k and 1/ X_∞) are obtained as 0.7946 and 0.3605 respectively using ‘nlinfit’ routine and using the parameter estimates the biomass values are predicted at different periods of times with neural networks, GRNN was used to predict the biomass values. Several iterations were conducted with different spread values ranging from 0.1 to 1.0. A larger spread leads to a large area around the input vector where first layer neurons will respond with significant outputs. If the spread is small the function is very steep, so that the neuron with the weight vector

closes to input will have a much larger output than other neurons. Finally, with a spread value of 0.2, we could achieve the predicted values which are almost identical to the experimental values (Figure 1).

Figure 1 represents the fitting of growth rate data using ANN and logistic equation. The solid line, dotted line, the circles represent the ANN curve, logistic curve and experimental data respectively. It is evident from Figure 1 that ANN curve best fits with the experimental data curve when compared to logistic curve. Thus logistic equation is not adequate in fitting the data.

4. CONCLUSIONS

A comparative study has been made for the fitting of growth rate data of Yarrowia lipolytica NCIM 3589 using logistic equation and GRNN respectively. It is found that logistic equation is poor in fitting the growth data when compared to ANN. Thus ANN was found to be superior in describing the growth characteristics of the organism.

REFERENCES