Wireless Engineering and Technology
Vol.3 No.3(2012), Article ID:21470,7 pages DOI:10.4236/wet.2012.33022
Design and Modeling of Electromagnetic Impedance Surfaces to Reduce Coupling between Antennas
1Center for Computational Nanosciences, Department of Physics and Astronomy, Ball State University, Muncie, USA; 2Department of Electrical Engineering, Advanced Teachers’ Training College for Technical Education, University of Douala, Douala, Cameroon; 3Department of Informational Statistics, Kyungsung University, Busan, Korea.
Email: ysjoe@bsu.edu
Received March 22nd, 2012; revised April 18th, 2012; accepted April 26th, 2012
Keywords: Coupling; Waveguide; Impedance Structure; Electromagnetic Compatibility
ABSTRACT
We study the coupling problem of two waveguide antennas using the design of a two-dimensional inhomogeneous impedance structure with a fixed reflected field. Since this structure enables electromagnetic compatibility between antennas located on a plane, the behaviors of the electromagnetic field along the impedance structure are investigated. The method of moments is used to solve the integral equations and the numerical results are presented and analyzed. To reduce coupling between antennas, we need to take into account both the amplitude distribution of the field along the structure and in the openings of the antennas. In addition, while designing the structure, it is necessary to control the coefficient of decoupling.
1. Introduction
During last decade, the process of development of radio electronics, radio location, radio navigation, and radio communication worldwide was characterized by the following basic tendencies: technical realization of enhanced physical effects and technical solutions, aspiration to accomplish transmission and information processing in real time with the broad use of computers, and the expansion of the applications solved by technology. As a consequence, despite micro-miniaturization of radio electronics facilities (REF), the volume occupied by such equipment on mobile and stationary objects is increasing [1,2]. The progression of these modern trends is vitally necessary, but it aggravates even more the serious problem of the provision in radio engineering complexes (REC) of electromagnetic compatibility, which is understood as the ability of REF and REC to function together with limited degradation of their own essential parameters and features.
Practically, it is often required to provide significant decoupling between the receiving and transmitting antennas, located on a common surface at a small distance from each other. One of the most well-known ways to reduce coupling between antennas is the application of electromagnetic bandgap (EBG) structures [3-8]. The EBG structures have received increased attention in recent years [9] in the areas of the microwave application. For example, a corrugated metal surface may be viewed as a structure consisting of infinitely many identical cavities, each having an aperture that is open to the air half-space. The EBG property emerges by virtue of periodic reactive loading of the guiding structure. As shown in papers [10-13], the most effective solution to the problem of providing minimum coupling between antennas is to present and resolve inverse problems of electrodynamics.
In this paper, we re-visit the bandgap structure and present another interesting mathematical model for designing the structure and suppressing surface waves on metals. In addition, we examine the possibility of reducing the coupling between antennas located on the plane, using an inhomogeneous synthesized impedance. In particular, we investigate the design problem of the impedance surface when an infinite thread of in-phase magnetic current is located above the plane at a certain height, and also the case with its location right on the impedance surface. Finally, the behaviors of the complete field on the impedance surface and the decoupling level between antennas are also investigated.
The paper is organized as follows: in Section 2, we consider a solution to the problem of synthesis of an inhomogeneous impedance plane by a fixed reflected field.
A solution to the problem of coupling of antennas on an impedance plane is given in Section 3, and numerical results are discussed in Section 4. Finally, Section 5 is devoted to conclusions.
2. Design of Impedance Surface@NolistTemp#2.1. Statement of the Design Problem
First, we consider a solution to the two-dimensional design problem for the arrangement shown in Figure 1. Above the plane
, there is an infinite thread of in-phase magnetic current 
located at the height
. On the surface
, the boundary impedance conditions of Shukin-Leontovich are fulfilled:
, (1)
where 
is the unit normal to the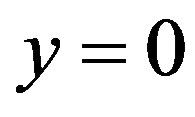 
plane, 
is the surface impedance, 
is the electric field, and 
is the magnetic field.
It is necessary to determine the dependence of the passive impedance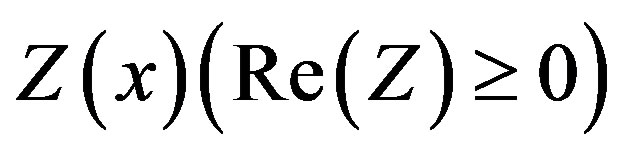 
on the surface S. Once Z(x) is obtained, the complete field in the upper space is found, and then the degree of decoupling between antennas can be obtained.
coincides with the impedance plane. Then, axis 
is directed parallel with the thread of the current, as shown in Figure 1. Further, we present the fields 
and 
on the surface as a sum of the incident and the reflected fields, respectively; 
, (2)
where 
and 
are reflected fields, 
and
. Here, 
is the ze-
Figure 1. Geometry of the design problem. The magnetic current Jm·ex is located at the height h.
roth-order Hankel function of the second kind, 
is the wave number, 
is the wavelength, 
is the imaginary unit, 
is the characteristic resistance of free space, 
, and 
is the first order Hankel function of the second kind.
The reflected field can be written as a sum of the reflected field 
in the fixed horizontal direction and the mirror-image field 
with unknown amplitude [13]:
and
where 
and 
are field vector components of an imaginary mirror source, 
and 
are field vector components of the given reflected fields. The solution to the design problem given in this paper differs from the solution in [13] by the fact that there is no supposition of a large value of the distance
, since the solution of reducing coupling between antennas in close proximity is of primary importance. The sense of this representation will become clear with further observation.
We now consider the analytical presentation of the distributed field on the 
plane. As long as the amplitude of the plane wave does not vary along the direction of its distribution, then for the reflected field in the direction
, it is possible to write:
, (3)
where 
is the distribution of the scattered field on the surface
. We represent the mirrorimage field on the impedance plane as the following way:
where 
is the constant amplitude. Then, the summative magnetic field on the surface 
can be written
, (4)
where
. From the first Maxwell equation, neglecting the derivative multiplier 
and
, we obtain for 
normalized on
:
(5)
where
. As a result, for the required impedance normalized on
, we also have:
(6)
where 
and
. In the general case, the resulting correlation gives the dependence of the passive impedance which gives a real part that can acquire positive as well as negative values.
Next, let us consider the design problem of the purely reactive impedance
. Presenting the correlation of Equation (6) as a real and imaginary part, we can obtain the condition of feasibility of purely reactive impedance:
(7)
An additional degree of freedom in the form of a mirror-image field 
gives an opportunity to realize the impedance structure with 
[13]. In this case, it is possible to find the impedance in the elegant form:
, (8)
where 
and 
is an angle of reflection. When the source of the field in Equation (6) is located right on the impedance surface
, which provides a completely normal (at the angle
) reflection of the incident wave (without a mirror-image,
), the required impedance can be expressed:
, (9)
where 
and
. From the condition of purely reactive impedance feasibility
it is not difficult to find the variation of the wave reflected from the inhomogeneous impedance plane,
:
, (10)
where
. In this case, the impedance can also be found from a straightforward expression:
, (11)
where
, 
and 
are the zeroth and first-order Bessel functions, respectively, and 
and 
are the zeroth and firstorder Neumann functions, respectively.
3. Model Analysis
The fact that variation of the surface impedance causes radiation of energy can be used to increase the decoupling between antennas, as well as to reduce the backscattering of the antennas. An example of a similar application of the surface impedance appears in Figure 2. Here, the resulting surface impedances change sharply, which brings about considerable decrease in current (because of re-radiation and reflection) flowing beyond the edge of the aperture or arriving at the second antenna.
The general system studied in this section has two aperture antennas in the shape of the open ends of parallel-plate waveguides (transmitting and receiving ones) with opening sizes of a and b, which are located on the y = 0 plane at a distance L from each other. On the y = 0 plane, several boundary conditions of Shukin-Leontovich [Equation (1)] are fulfilled. To solve the problem of analysis, we use the Lorentz lemma in the integral form for each of the three areas:
, 
, and
, shown in Figure 2, i.e., by defining the field excited in the upper half-space (region
), the radiating waveguide (region
), and the receiving (region
) waveguide [14]. Then we can obtain a system of integral equations relative to the unknown tangential components of the electric field on the surface (
and
) by taking into account the boundary conditions on the surface of the impedance flanges and the equality of the tangential field components in the openings of the waveguides
(
in
;
in
):
(12)
Figure 2. The general system studied has two aperture antennas in the shape of the open ends of parallel-plate waveguides (transmitting and receiving ones) with opening sizes of a and b, which are located on the y = 0 plane at a distance L from each other. The system is composed of three regions: V1, V2, and V3.
where the subsidiary magnetic fields
, 
, and 
are solutions of the nonuniform Helmholtz equations for complex amplitudes of the vector potentials for regions
, 
, and
, respectively. In this way, the fields in the opening of the antennas and on the impedance part of the flange can be found. From this, the minimum level of coupling between the two antennas can then be determined.
It is necessary to note that development of an algorithm for the mathematical model under consideration is based on the specifics of the electric field at the edges 
and on the numerical solution of a system of integral equations through the KrylovBogolyubov method [15].
We next study the behavior of the complete field 
on the impedance surface as a function of its dimensions and the parameters, 
and
. In Figure 3, we show a graph of the variation of the impedance distribution [Equation (8)] with the following parameters: 
and 
(solid line), 
(dashed line), 
(dotted line). We see in Figure 3 that the impedance distribution which gives a nearly hyperbolic reactance is the one for the angle
. For
, the reactance remains zero for most of the interval, and for
, the reactance is only slightly below zero. At the end of the interval [0, 0.66λ], the curve is undefined (it becomes infinite) for
.
Figures 4(a) and (b) show the dependence of
, normalized relative to the field 
above an ideal conducting plane for fixed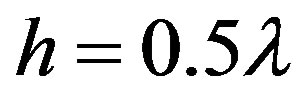 
and various angles:
Figure 3. Variation of impedance distribution relative to Equation (8) for fixed h = 0.5λ and different angles: φ0 = 30˚ (solid line), φ0 = 45˚ (dashed line) and φ0 = 60˚ (dotted line). The length of the structure is L = λ. The impedance distribution which gives a reactance with a nearly hyperbolic character is the one for the angle φ0 = 60˚.
(a)
(b)
Figure 4. (a) Behavior of the complete field along the structure for fixed h = 0.5λ and various angles: φ0 = 30˚ (solid line), φ0 = 45˚ (dashed line) and φ0 = 60˚ (dotted line); (b) Behavior of the complete field along the structure for φ0 = 45˚ and h = 0.4λ (solid line); h = 0.5λ (dashed line) and h = 0.6λ (dotted line). The length of the structure is L = λ for both cases. The largest decoupling level is obtained with the parameters: φ0 = 60˚ and h = 0.5λ.
(solid line), 
(dashed line) and 
(dotted line); and for the fixed angle 
with various values of the parameter, 
(solid line), 
(dashed line) and 
(dotted line), respectively. The length of the impedance structure is equal to 
for both cases. The results of calculations show that the best data (greatest decoupling) are obtained with the parameters 
and 
when the impedance acquires the greatest capacitive value near the source of radiation. The greatest decoupling level is obtained with 
and
. The synthesized impedance which gives appropriate results for increased decoupling should be taken into account, because it has a large negative value of the reactive part in close proximity to the antenna. This leads to the fact that the impedance practically creates an anti-phase field relative to the ideal conducting surface. As a result, all the energy of the electromagnetic field transfers into the energy stored around the antenna. The structure turns into a resonator without losses (for the reactive impedance), including radiation. As an example, Figure 5 shows the radiation patterns 
of the antenna located above the ideal conducting surface (dashed line) and the impedance surface (solid line) with the parameters: 
and
. From the graph, it is apparent that decoupling is provided with reduction of the radiation field by 35 dB; i.e., a reduction of the main lobe of the radiation pattern.
Figure 6 shows the variation of the impedance distribution relative to Equation (11). The resulting impedance distribution is nearly flat (crossing zero at 
and
), except for a sharp Fano-type variation at
. The reactance reaches its minimum point with a capacitive reactance of 60, and sharply transitions to a maximum inductive value of 60. The behavior
Figure 5. Radiation patterns of the antenna located above the ideal conducting (dashed line at 0 dB) and impedance (solid line) surfaces. The parameters for the calculation are: φ0 = 60˚ and h = 0.5λ. The graph shows that the decoupling is provided with reduction of the radiation field by 35 dB for the main lobe of the radiation pattern.
of the complete field along the structure relative to Figure 6 is also shown in Figure 7 where the normalized impedance at point 
acquires a value close to
. The dash-dotted line shows this case. The dashed and solid lines correspond to the limiting maximum impedance values of 100 and 50, respectively. The dotted curve shows the case with negative impedance limited to the value –50. As we can see, field reduction in this case surpasses all the rest. It is evident that the main factor in increasing the decoupling is not the variation of the impedance distribution, but its limiting value near the antenna. This value leads to the appearance of an anti-phase reflected field, i.e., to a sharp reduction of the radiation field. At the same time, research into the behavior of the complete field along the impedance structure in Figures 4 and 7 shows that behind the structure on the region of the surface with zero impedance, the intensity of the magnetic field 
sharply increases like the behavior of the field above an inhomogeneous reactance. Analogous phenomena are considered on all regions where the value of the reactance approaches zero or
Figure 6. Variation of the impedance distribution relative to Equation (11).
Figure 7. Variation of the complete field along the structure relative to the impedance distribution obtained in Figure 6. The dash-dotted curve is the case when the limiting value of the maximum impedance is 500. The dashed and solid curves correspond to limiting values of 100 and 50, respectively. The dotted curve shows the case with negative impedance limited to the value –50. The field reduction for the negative impedance gives the best results.
acquires positive values. Let us note that in Figure 7, the resulting field distributions have oscillatory behavior.
Next, we consider the possibility of designing decoupling structures on the basis of the impedance structure synthesized above, i.e., taking into account the aperture of the receiving antenna. Figure 8 shows the distribution of the complete field normalized to the amplitude of the path wave of the radiator in the openings of waveguide antennas 
and along the structure 
for the impedance calculated by Equation (8) for the parameters, 
and 
(dashed line) (
dB, the coefficient of standing waves (CSW)
); 
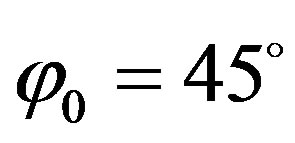(dotted line) (
dB,
); 
(dash-dotted line) (
dB,
). The solid line corresponds to the ideal conducting structure. As we can see, the angle, 
, which provides a higher level of decoupling, has a large CSW value of 2.36, because of large capacitive reactance near to the antenna opening. Such a structure is of a little use for near-omnidirectional transmitting antennas. In order to decrease the CSW, it is necessary to move the impedance structure aside from the antenna opening so that there is zero or low inductive reactance near the opening. On the other hand, the CSW is better when the angle is
. Unfortunately, in this case, the coefficient of decoupling is smaller. It is important to note that in the presence of the ideal conducting surface, the weakening of the field is half as large during coupling along the geodesic line.
Distribution of the impedance for the structure which provides the greatest decoupling is shown in Figures 9(a) 
and (b)
. The dimensions
are similar for both cases. The resulting impedance distributions are parabolic in some small intervals. As in Figure 3, they don’t have any points at the
Figure 8. Distribution of the complete field for the impedance calculated by Equation (8) for the parameters, a = b = 0.34λ, h = 0.5λ and φ0 = 30˚ (dashed line, CSW = 2.37); φ0 = 45˚ (dotted line, CSW = 2.32); φ0 = 60˚ (dash-dotted line, CSW = 2.36). The solid line corresponds to the case of an ideal conducting surface. As is evident, the angle, φ0 = 60˚, which provides a better level of decoupling has a large CSW value of 2.36, due to a large capacitive reactance near to the antenna opening.
(a)
(b)
Figure 9. (a) Distribution of the impedance for the structure which provides the greatest decoupling for the parameters, h = 0.5λ, φ0 = 60˚ and L = λ; (b) The same distribution is also presented for these parameters, but with L = 2λ. The dimensions a = b = 0.34λ are similar for both cases. The resulting impedance distributions are parabolic in some small intervals.
extremities and outside of the interval. As we can see, increasing the size of the structure to 
only doubled the scale of the positive value of the reactance, without changing the character of its distribution. The value of the field in the opening of the receiving antenna (Figure 10) has somewhat grown. However, the level of decoupling has nevertheless increased by 3 dB, becoming equal to 43.4 dB. To explain this fact, Figure 11 shows the distributions of the real (solid line) and the imaginary (dashed line) components of the complete field. It is clear that both components of the field in the opening of the receiving antenna are very weak, and consequently, their impact on the main wave in the receiving antenna is not significant. In this connection, it is possible to state that there is no opportunity to completely characterize the degree of decoupling between antennas solely on the basis of the amplitude distribution of the field along the structure and in the openings of the antennas. During the designing of decoupling structures, it is necessary to also control the coefficient of decoupling
, where 
is the coefficient of antenna coupling. We also note that, as in Figure 7, the distribution of the field in Figure 10 has oscillating, non-monotonic behavior.
Figure 10. Distribution of the field relative to Figure 9(b). The resulting field distribution has oscillating, non-monotonic behavior.
Figure 11. Distribution of the complete field relative to Figure 9(b), showing the real (solid line) and the imaginary (dashed line) components. It is clear that both components of the field in the opening of the receiving antenna are very weak.
Nevertheless, we can consider the results of antenna decoupling using the structure giving the impedance distribution presented in Figure 12, as calculated by Equation (11) for the same system parameters as in Figure 8. The resulting impedance distribution has a reactance close to the character of the tangent function. Beyond the receiving antenna, the impedance distribution is inverted. With this level of decoupling, this structure gives the same result (
dB) as in the previous case for the structure with the parameters: 
and 
(see Figure 8, solid line) shown in Figure 13. We note that Figure 13 also has oscillating, non-monotonic behavior. Finally, we mention that the optimization of the impedance decoupling structures is ideally fulfilled not by the level of the field distributed along the synthesized structure (although this also gives some positive results), but by the level of decoupling
, or more exactly, by the level of the main wave 
in the receiving antenna.
5. Conclusions
In summary, we have solved the problem of designing a heterogeneous impedance plane given a stated reflected
Figure 12. Variation of the impedance calculated by Equation (11). The parameters for our calculation are a = b = 0.34λ, L = λ, h = 0.5λ and φ0 = 60˚. The resulting impedance distribution has a reactance close to the character of the tangent function. Beyond the receiving antenna, the impedance distribution is inverted.
Figure 13. Distribution of the complete field relative to Figure 12. The parameters for our calculation are the same as in Figure 8. The resulting field distribution has oscillating, non-monotonic behavior.
field. We obtained the variation of the impedance distribution of the purely reactive surface in explicit form. The calculations show that the best results are given by the parameters, 
and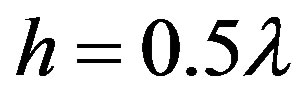
, for which the impedance acquires large capacitive values near the source of radiation. However, during the solution of the design problem, the interaction between antennas was not taken into account. It is evident that the presence of the receiving aperture antenna will lead to unwanted reduction of antenna decoupling by means of the heterogeneous features created by the very aperture of the receiving antenna.
Taking into account the receiving antenna, we found a solution to the problem of analysis of the EMF of two waveguides antennas located on the same impedance plane on the basis of the impedance designed in Section 2. The calculated result has shown that to limit coupling between antennas, we need to take into consideration both the amplitude distribution of the field along the structure and in the openings of the antennas. Moreover, during the designing of the structure, it is necessary to also control the coefficient of decoupling.
REFERENCES
- K. G. Klimachev, “Fundamentals of Forecasting and Provision of Electromagnetic Compatibility of Radio Engineering Systems and Devices,” Moscow Aviation Institute, Moscow, 1994.
- A. I. Sapgira, “Electromagnetic Compatibility of Radio Electronic Devises and Unpredicted Interferences, Vol 1: General Questions of EMC,” Soviet Radio, Moscow, 1977.
- N. C. Karmakar and M. N. Mollah, “Potential Applications of PBG Engineered Structures in Microwave Engineering: Part I,” Microwave Journal, Vol. 47, No. 7, 2004, pp. 22-44.
- P. S. Kildal, “Artificially Soft and Hard Surfaces in Electromagnetics,” IEEE Transactions on Antennas and Propagation, Vol. 38, No. 10, 1990, pp. 1537-1544. doi:10.1109/8.59765
- P. S. Kildal, A. A. Kishk and A. Tengs, “Reduction of Forward Scattering from Cylindrical Objects Using Hard Surfaces,” IEEE Transactions on Antennas and Propagation, Vol. 38, No. 10, 1990, pp. 1537-1544. doi:10.1109/8.59765
- R. E. Lawrie, “The Control of the Echo Area of Ogives by Cutoff Corrugated Surfaces,” IEEE Transactions on Antennas and Propagation, Vol. 14, No. 6, 1966, pp. 798-799. doi:10.1109/TAP.1966.1138802
- J. Carlsson and P. S. Kildal, “Transmission through Corrugated Slots,” IEEE Transactions on Electromagnetic Compatibility, Vol. 37, No. 1, 1995, pp. 114-121. doi:10.1109/15.350251
- R. B. Hwang and S. T. Peng, “Surface-Wave Suppression of Resonance-Type Periodic Structures,” IEEE Transactions on Antennas and Propagation, Vol. 51, No. 6, 2003, pp. 1221-1229. doi:10.1109/TAP.2003.811470
- G. Goussetis, A. P. Feresidis and P. Kosmas, “Efficient Analysis, Design, and Filter Applications of EBG Waveguide with Periodic Resonant Loads,” IEEE Transactions on Microwave Theory and Techniques, Vol. 54, No. 11, 2006, pp. 38853892. doi:10.1109/TMTT.2006.883648
- Y. S. Joe, J.-F. D. Essiben, E. R. Hedin, J. T. N. Bisse and J. Mаtаngа, “Optimization of Impedance Plane Reducing Coupling between Antennas,” Wireless Engineering and Technology Journal, Vol. 2, No. 1, pp. 1-8, 2010. doi:10.4236/wet.2011.21001
- Yu. V. Yukhanov, “Analysis and Synthesis of Impedance Plane,” Radiotechnics and Electronics, Vol. 45, No. 4, 2000, pp. 404-409.
- A. Yu. Yukhanov, “Synthesis of Reactance Anisotropic Plane Excited By a Thread of In-Phase Magnetic Current,” International Conference on Radiation and Scattering of Electromagnetic Waves, Taganrog, 20-25 June 2005, pp. 360-362.
- A. Yu. Yukhanov, “Two-Dimensional Task of Impedance Plane Synthesis,” Radio Engineering Circuits, Signals and Devices, Vol. 45, 1998, pp. 92-95.
- Y. S. Joe, J-F. D. Essiben and E. M. Cooney, “Radiation Characteristics of Waveguide Antennas Located on the Same Impedance Plane,” Journal of Physics D: Applied Physics, Vol. 41, No. 12, 2008, Article ID: 125503. doi:10.1088/0022-3727/41/12/125503
- O. N. Tereshin, V. M. Sedov and A. F. Chaplin, “Synthesis of Antennas on Decelerating Structures,” Communication Press, Moscow, 1980.