Journal of Electromagnetic Analysis and Applications
Vol.4 No.11(2012), Article ID:25110,4 pages DOI:10.4236/jemaa.2012.411065
1Department of Electronics and Communication, Dharmsinh Desai University, Nadiad, India; 2Antenna Systems Area, Space Applications Center, ISRO, Ahmedabad, India; 3Department of Electrical and Computer Engineering, University of Iowa, Iowa City, USA.
Email: rizwan_alad@yahoo.com, soumya@sac.isro.gov.in, *Lonngren@engineering.uiowa.edu
Received August 30th, 2012; revised September 28th, 2012; accepted October 10th, 2012
Keywords: Elliptical Metallic Plate; Capacitance; Pulse Function; Point Matching
ABSTRACT
This paper presents the evaluation of the capacitance of an isolated elliptical plate and two parallel elliptical plates. Integral equations are formed by relating the previously unknown charges on the elliptical plates and the potential on the metallic plates. The integral equations are solved by applying the method of moments based on the pulse function and point matching. The elements of the matrix in the method of moments are found by dividing the structure into triangular subsections. The matrix equation is solved in order to compute the unknown charges on each subsection. Numerical results on the capacitance as a function of the geometrical parameters of the ellipse are presented.
1. Introduction
The evaluation of the capacitance of various structures having different geometrical shapes is of importance to study the behavior of electrostatic charge build-up on bodies that are isolated in space such as space-craft structures in orbit. The analysis of three-dimensional spherical, paraboloidal and truncated conical surfaces and two-dimensional square, rectangular, circular and annular metallic disks have been examined using the method of moments [1-6]. In these works, the capacitance of the different geometrical structures was obtained by subdividing the structure into uniform rectangular planar subsections and computing the effect of the charge on each subsection on the potential of the others. The use of rectangular subsection in a curved boundary requires a very fine meshing in order to obtain convergence for the data of the capacitance and charge distribution. Meshing with triangular elements on the other hand facilitates the mapping of the geometrical boundaries of arbitrary shape very accurately [7]. The meshing techniques employed in [3] are limited by the large ratio of the area of the biggest elements to smallest elements, which possibly results in an unstable solution.
This paper presents the analysis of a planar elliptical metallic plate isolated in free space as well as two parallel elliptical plates using the method of moments in which triangular sub-areas were used for the solution of integral equations. A closed form expression for the capacitance of a single elliptical conducting plate has been reported by Liang et al. [8]. They did not present any data on the capacitance for the case of two parallel elliptical plates of finite size. Thus it is worthwhile to carry out the analysis of elliptical structures using the method of moments with triangular subsections for the geometry under consideration unlike that reported in [1-6].
In order to apply the method of moments, the elliptical plate is divided into a number of triangular elements. The unknown charge distribution on the surface of the elliptical plates appears in the form of an integral equation relating the potential function and charge distribution. This integral equation is solved using the method of moments formulation based on a pulse function and point matching. The methods of finding the diagonal and the non-diagonal elements of the matrix are presented. The capacitance is calculated as a function of eccentricity of the ellipse for a unit semi major axis. The validity of the analysis is justified by comparing the data on the capacitance using the present method with that of the closed form expression in [8].
2. General Analysis
2.1. Single Elliptical Plate
Figure 1 shows a single elliptical plate with a semi major axis a and semi minor axis b. In order to compute the capacitance of this structure, the plate is subdivided using triangular elements as shown in Figure 2. The unknown surface charge density on the plate at any point 
is denoted by
. It is assumed that the surface charge density is constant over each subsection
Figure 1. Geometry of a single elliptical plate.
Figure 2. Subdividing an elliptical plate with triangular elements.
so that the charge on each element can be represented by pulse basis functions. The potential at any point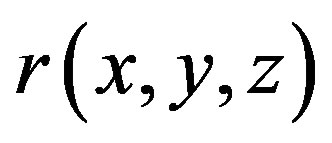 
due to the charges of the plate is expressed as follows
(1)
Assuming that the metallic plate is a perfect conductor, the surface will be an equipotential surface (f = V which is the assumed potential of the plate), the above equation forms an integral equation with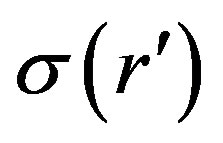 
being as yet unknown. The surface charge density 
can be expressed as [9]
(2)
where N is the number of triangular elements, an are the unknown coefficients and fn are the pulse basis functions given by
(3)
where Dsm and Dsn are the areas of the mth and nth triangular elements respectively.
Substituting Equation (2) into Equation (1) and satisfying the resultant equation at the centroid of each triangular element, the following expression is obtained
(4)
The potential at the centroid of each triangular subsection in terms of an integral can be expressed which can also be reduced to a summation where Lmn represents the potential at point m due to charge at the subsection n. The Equation (5) can be written in matrix equation form as follows
(5)
where
(6)
and
is the area of the mth triangular element.
For m = n, this expression for the matrix element is not valid. Thus the diagonal elements have to be treated separately [6]. The diagonal elements are calculated by considering each triangular section to be a circle of equal area. Then the diagonal element is given by [10]
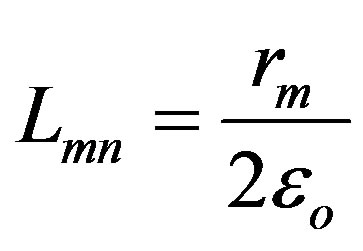(7)
which corresponds to the potential of a uniformly charged circular disk of radius rm at the edge of the disk.
The matrix equation can be solved to determine the unknown coefficients as follows
(8)
The total charge can be computed from
(9)
where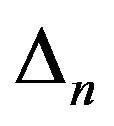 
is the area of nth triangular element.
The capacitance can be computed from
(10)
2.2. Parallel Elliptical Plates
Consider two parallel metal elliptical plates 
and 
separated by a distance 
as shown in Figure 3. Let the potential at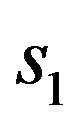 
be V1s and the potential at 
be V2s. The unknown quantities in this case are the charge distributions 
and 
over the surfaces 
and
. Let 
be discretized by N elements and 
from N + 1 to 2N elements. The discretization is shown in Figure 4. Let the total charge be 
and 
on the surfaces 
and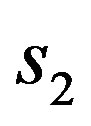 
respectively.
Using superposition and the relationship between the
Figure 3. Geometry of parallel elliptical plates.
Figure 4. Subdividing parallel elliptical plates with triangular Elements.
charge and the potential [8], we have
(11)
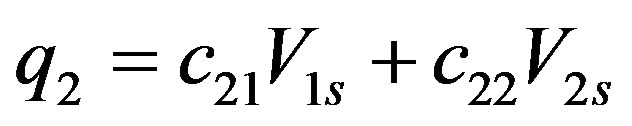(12)
where
Equations (11) and (12) can be expressed in the matrix equation form as
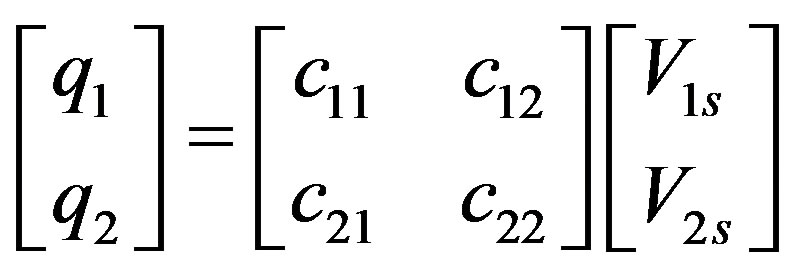(13)
If V1 is the potential on 
due to 
and 
is the potential on 
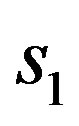due to
, then the potential
(14)
If 
is the potential on 
due to 
and 
is the potential on 
due to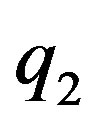
, then the potential of 
is
(15)
Equations (14) and (15) are two integral equations which can be solved using the same procedure that was used for the isolated ellipse case as given in section A. applying the pulse function and point matching techniques, the following sets of equations are obtained
(16)
where
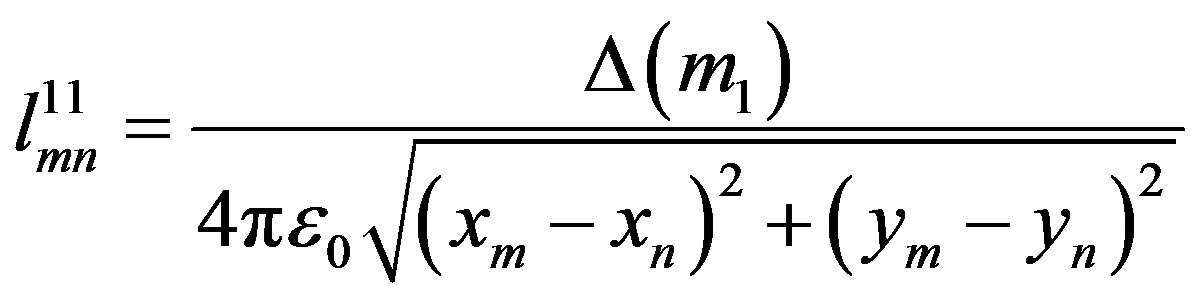(17)
(18)
(19)
(20)
In Equations (17)-(20), 
is the area of the mth triangular element of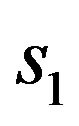 
and 
is the area of the mth triangular element of
. The diagonal elements are similarly obtained by assuming that the triangular element is replaced with a circle with the equivalent area and the potential at the edge of a circle is computed. The diagonal element is given by [9]
(21)
where r is the radius of the equivalent circle.
The above set of simultaneous equations can be written in matrix equation form as follows
(22)
The solution of Equation (22) is obtained as
(23)
where xmn are the elements of inverse of the square matrix of Equation (22). Comparing Equations (13) and (23), the elements of the capacitance matrix in (13) are obtained as the sum of the elements of each sub matrix of Equation (23).The capacitance of the structure of Figure 3 is determined by [9]
(24)
3. Numerical Analysis
Using Equations (6)-(8), the matrix elements and the unknown coefficients are calculated assuming that the potential of the plate is equal to 1. Using Equations (8) and (9), the capacitance of an elliptical isolated disk with eccentricity e = 0.85 has been calculated. The convergence of the computed numerical values is illustrated in shown in Figure 5. The converged value of the capacitance is 49.873 pF. The computed capacitance as a function of eccentricity is presented in Figure 6 and the numerical value of the capacitance is presented in Table 1. The numerical results can be compared with a closed form solution for a circular disk (eccentricity=0) in Table 1 [8].
Using Equations (17)-(23), the matrix elements and the unknown coefficients are calculated assuming the upper plate is at potential Vs1 = +1 while the potential on the lower plate is Vs2 = –1 with various values of eccentricity and separation distance between the plates. Using Equation (24), the capacitance of parallel elliptical plates separated by a distance d = 1 and e = 0.85 has been
Figure 5. Convergence of data on capacitance for an isolated elliptical plate.
Figure 6. Capacitance of a metallic isolated elliptical plate as function of eccentricity of unit semi major axis.
Table 1. Numerical Value of Capacitance Data with Function of Eccentricity.
calculated to check the convergence of the data on capacitance. The convergence of the data on the capacitance has been checked by increasing the number of subsections and the converged value of the capacitance is 39.263 pF. The convergence data is shown in Figure 7. The capacitance values for various eccentricities are presented in Figure 8. The numerical value of the capacitance for two parallel circular disk (eccentricity = 0) with d = 1 is 63.378 pF as shown in Figure 8. The numerical value of the capacitance is computed as a function of distance and is presented in Table 2. Figure 9 shows the variation of the capacitance normalized by the closed from of the simplified expression eA/d (C0), where A is the area of the ellipse as a function of A/d.
4. Discussion and Conclusions
This investigation demonstrates that convergence can be obtained for an elliptical plate for a finite number of elements which is approximately 725 elements for an isolated elliptical plate. With this number, the convergence achieved is at the fourth decimal place. The capacitance of an isolated elliptical plate decreases mono-
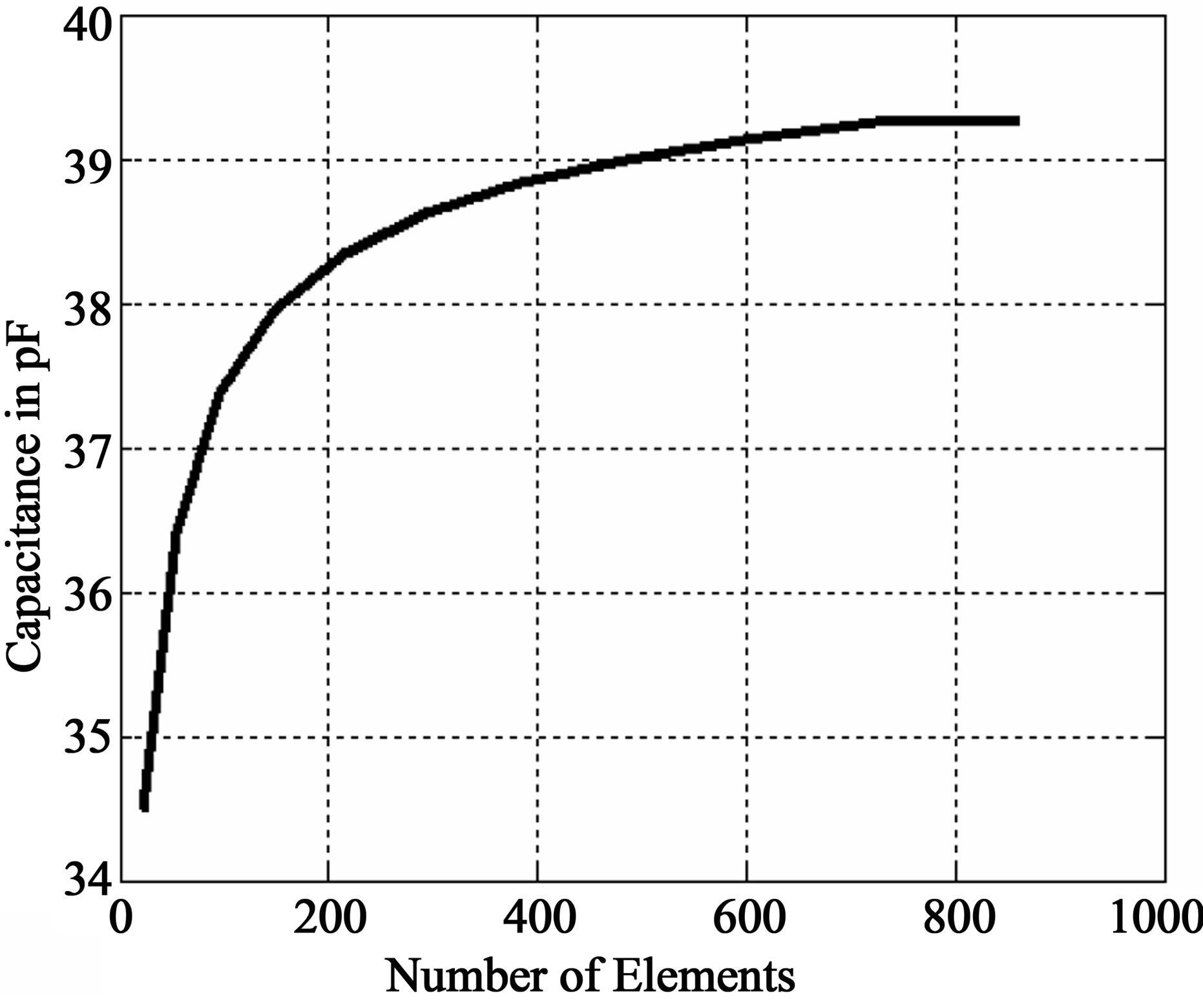
Figure 7. Convergence of parallel elliptical plates (d = 1).
Figure 8. Capacitance of parallel elliptical plates as function of eccentricity of unit semi major axis.
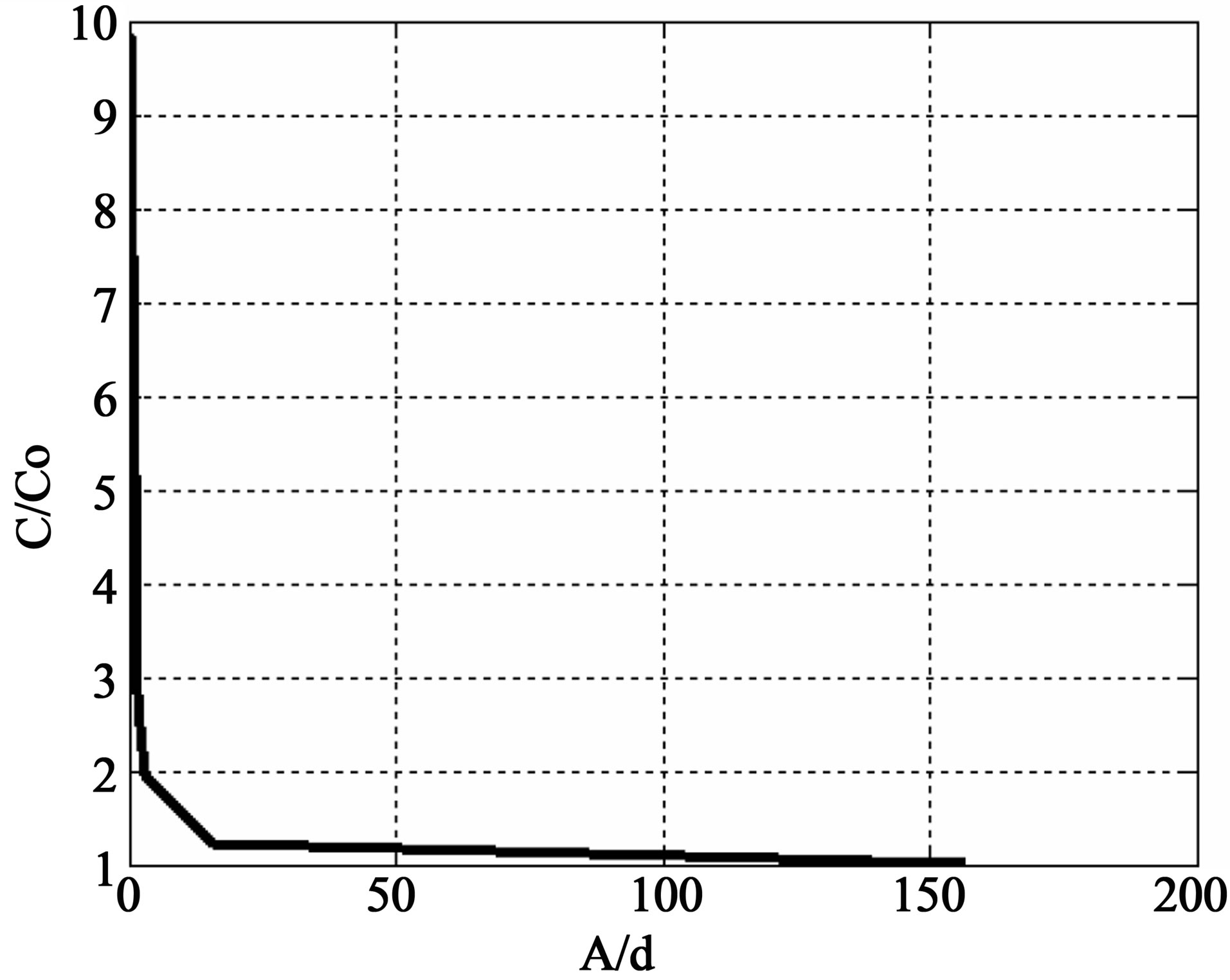
Figure 9. Capacitance of parallel elliptical plates as function of A/d.
tonically with an increase in eccentricity. If the eccentricity = 0 which is the case of a circle, the results can be compared with an analytical result.
When the eccentricity = 0, which is a case of a circle, the result obtained by this technique is 6.90e-011 F which is very close to the approximate closed form expression of capacitance 8e0 for a circular disk of unit radius [11]. Figure 7 shows that the convergence of the parallel ellipse occurs at 863 elements at the third decimal point. Figure 8 shows how the capacitance of a parallel elliptical plate decreases monotonically with an increase in eccentricity. The data presented in Table 2 depicts that there is a decrease in the capacitance with an increase in the distance between the metallic elliptical plates. For the further validation, Figure 9 shows that C/C0 decreases as A/d increases, for very large A/d, which corresponds to the fringeless case, the ratio of C/C0 is very close to unity.
5. Acknowledgements
The first author thanks the Vice Chancellor of Dharmsinh Desai University, India for his support and encouragement. The authors also express gratitude to Dr. Nikhil Kothari for his personal support in terms of providing the required environment and facilities to carry out this work.
REFERENCES
- B. N. Das and S. B. Chakrabarty, “Capacitance and Charge Distribution of Two Cylindrical Conductors of Finite Length,” IEEE Proceedings of Science, Measurement and Technology, Vol. 144, No. 6, 1997, pp. 280- 286. doi:10.1049/ip-smt:19971424
- S. Ghosh and A. Chakrabarty, “Estimation of Capacitance of Different Conducting Bodies by the Method of Rectangular Subareas,” Journal of Electrostatics, Vol. 66, No. 3-4, 2008, pp. 142-146.
- B. N. Das and S. B. Chakrabarty, “Capacitance of a Truncated Cylinder,” IEEE Transaction on Electromagnetic Compatibility, Vol. 39, No. 4, 1997, pp. 371-374.
- B. N. Das and S. B. Chakrabarty, “Capacitance of Metallic Structures in the Form of Parabloidal and Spherical Reflectors,” IEEE Transaction on Electromagnetic Compatibility, Vol. 39, No. 4, 1997, pp. 390-393.
- E. W. Bai and K. E. Lonngren, “Capacitors and the Method of Moments,” Computers and Electrical Engineering, Vol. 30, No. 3, 2004, pp. 223-229. doi:10.1016/j.compeleceng.2002.10.002
- C. O. Hwang and M. Mascagni, “Electrical Capacitance of the Unit Cube,” Journal of Applied Physics, Vol. 95, No. 7, 2004, pp. 3798-3802. doi:10.1063/1.1664031
- R. T. Fenner, “FEM Method for Engineers,” Imperial College Press, London, 1996, pp. 71-88.
- C. H. Liang, L. Li and H. Q. Zhai, “Asymptotic Closed Form for the Capacitance of an Arbitrarily Shaped Conducting Plate,” IEEE Proceedings of Microwave, antennas Propagation, Vol. 151, No. 3, 2004, pp. 217-220. doi:10.1049/ip-map:20040273
- R. F. Harrington, “Field Computation by Moment Methods,” IEEE Press, New York, 1993. doi:10.1109/9780470544631
- A. T. Adams, “Electromagnetics for Engineers,” John Wiley & Sons Inc, Hoboken, 1971, pp 165-185.
- T. Itoh and R. Mitra, “A New Method for Calculating the Capacitance of a Circular Disk for Microwave Integrated Circuits,” IEEE Transactions on Microwave Theory and Techniques, Vol. 21, No. 6, 1973, pp. 431-432.
NOTES
*Corresponding author.