Applied Mathematics
Vol.3 No.12A(2012), Article ID:25997,7 pages DOI:10.4236/am.2012.312A282
Large and Moderate Deviations for Projective Systems and Projective Limits
Department of Sciences, Technical University of Crete, Chania, Greece
Email: tryfondaras@gmail.com
Received September 11, 2012; revised October 11, 2012; accepted October 18, 2012
Keywords: Large Deviations; Projective Systems; Projective Limits; Moderate Deviations
ABSTRACT
One of the active fields in applied probability, the last two decades, is that of large deviations theory i.e. the one dealing with the (asymptotic) computation of probabilities of rare events which are exponentially small as a function of some parameter e.g. the amplitude of the noise perturbing a dynamical system. Basic ideas of the theory can be tracked back to Laplace, the first rigorous results are due to Cramer although a clear definition was introduced by Varadhan in 1966. Large deviations estimates have been proved to be the crucial tool in studying problems in Statistics, Physics (Thermodynamics and Statistical Mechanics), Finance (Monte-Carlo methods, option pricing, long term portfolio investment) and in Applied probability (queuing theory). The aim of this work is to describe one of the (recent) methods of proving large deviations results, namely that of projective systems. We compare the method with the one of projective limits and show the advantages of the first. These advantages are due to the fact that: 1) the arguments are direct and the proofs of the basic results of the theory are much easier and simpler; 2) we are able to extend most of these results using suitable projective systems. We apply the method in the case of a) sequences of i.i.d. r.v.’s and b) sequences of exchangeable r.v.’s. All the results are being proved in a simple “unified” way.
1. Notation and Basic Results
Definition 1.1. Let E be a Hausdorff topological space, F a σ-algebra of subsets of E, and  (with D a directed set) a net of probability measures (p.m.’s) defined on F. We say that, the net of p.m.’s
(with D a directed set) a net of probability measures (p.m.’s) defined on F. We say that, the net of p.m.’s  satisfies the full large deviations principle ([1,2]), with normalizeing constants
satisfies the full large deviations principle ([1,2]), with normalizeing constants  (
( such that
such that
 ) and rate function
) and rate function , if I is lower semi-continuous and
, if I is lower semi-continuous and , we have:
, we have:
1) (upper bound)
 (1)
(1)
2) (lower bound)
 (2)
(2)
with cl(B) (int(B)) the closure (respectively the interior) of the set Β.
If, in addition,  (level set) is compact, I is called a good rate function.
(level set) is compact, I is called a good rate function.
Remark 1.2.
If the upper bound is valid for all compact sets, while the lower bound is still true for all open sets, we say that the net of p.m.’s  satisfies the weak large deviations principle.
satisfies the weak large deviations principle.
In order to “pass” from a weak LDP to a full LDP we have to find a way of showing that, most of the probability mass (at least on an exponential scale) is concentrated on compact sets. The tool for doing this, is the following.
Definition 1.3.
A net of p.m.’s  defined on (E,F) is called exponentially tight, if
defined on (E,F) is called exponentially tight, if  there is a compact set
there is a compact set  (subset of E) such that:
(subset of E) such that:
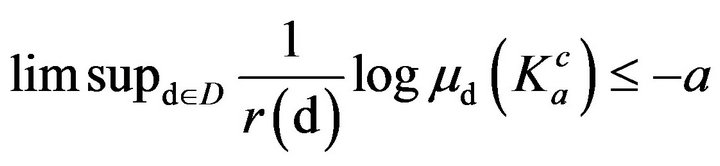 (3)
(3)
Exponential tightness is applied to the following proposition to strengthen a weak large deviations result. A proof of the proposition can be found in [1].
Proposition 1.4.
Let  be a net of p.m.’s defined on
be a net of p.m.’s defined on  that is exponentially tight.
that is exponentially tight.
Then: a) if the upper bound holds for all compact sets, then it also holds for all closed sets.
b) if the lower bound holds for all open sets, then the rate function is good.
Now, we will characterize families of topological spaces. This special kind of families will play an important role in proving large deviations results.
Definition 1.5. The family , with A a directed set, is called a projective system if:
, with A a directed set, is called a projective system if:
1)  is a Hausdorff topological space 2)
is a Hausdorff topological space 2)  is a continuous, subjective map such that, if:
is a continuous, subjective map such that, if:  Also,
Also,  is the identity map on
is the identity map on .
.
We also consider a Hausdorff topological space E, F a σ-algebra of subsets of E and  a continuous, surjective map s.t. if
a continuous, surjective map s.t. if 
and for then
then .
.
The following two theorems give large deviations results in the case of projective systems [3].
Theorem 1.6. Let E be a Hausdorff topological space, F a σ-algebra of subsets of E s.t.: a) F contains the class of compact sets and b) F contains a base U for the topology.
Let  be a projective system and
be a projective system and
 be as above. Assume that
be as above. Assume that  is measurable when E is endowed with F and
is measurable when E is endowed with F and  with the Borel σ-algebra. Let
with the Borel σ-algebra. Let  be a net of p.m.’s on F and assume that:
be a net of p.m.’s on F and assume that:
i) , the net of p.m.’s
, the net of p.m.’s ![]() satisfies a large deviations principle with normalizing constants
satisfies a large deviations principle with normalizing constants  and rate function
and rate function

ii) the net of p.m.’s  is exponentially tight.
is exponentially tight.
Then, the net  satisfies the large deviations principle with normalizing constants
satisfies the large deviations principle with normalizing constants  and good rate function
and good rate function .
.
When E is endowed with a specific topology (namely the topology induced by the maps ), Theorem 1.6 has the following form.
), Theorem 1.6 has the following form.
Theorem 1.7. Let E,  be as in theorem 1.6. Endow E with the initial topology induced by the maps
be as in theorem 1.6. Endow E with the initial topology induced by the maps  and let F be the σ-algebra of subsets of E such that
and let F be the σ-algebra of subsets of E such that  is measurable, where
is measurable, where  is endowed with its Borel σ-algebra
is endowed with its Borel σ-algebra . Let
. Let  be a net of p.m.’s on F and assume that:
be a net of p.m.’s on F and assume that:
i) , the net of p.m.’s
, the net of p.m.’s ![]() satisfies a large deviation principle with normalizing constants
satisfies a large deviation principle with normalizing constants  and rate function
and rate function 
ii) there is a function  such that
such that
 the set
the set is compact and
is compact and :
:

Then, the net of p.m.’s  satisfies the large deviations principle with normalizing constants
satisfies the large deviations principle with normalizing constants
 and good rate function Ι, and
and good rate function Ι, and
 .
.
On early days, large deviations results were proved using “large” spaces. One of these spaces is described below.
Definition 1.8. Let  be a projective system. The projective limit of this system (denoted by
be a projective system. The projective limit of this system (denoted by
 ) is the subset of the product space
) is the subset of the product space  which consists of the elements
which consists of the elements  for which
for which
 when
when , endowed with the topology induced by Υ ([2]).
, endowed with the topology induced by Υ ([2]).
The following basic result, analogous to that of Theorem 1.7, allows one to transport a large deviations result on a “smaller” topological space to a “larger” one.
Theorem 1.9. Dawson-Gärtner (large deviations for projective limits).
Let  be a net of p.m.’s defined on
be a net of p.m.’s defined on
 . Assume that
. Assume that , the net of p.m.’s
, the net of p.m.’s ![]() satisfies the full large deviations principle with constants
satisfies the full large deviations principle with constants  and good rate function
and good rate function . Then, the net of p.m.’s
. Then, the net of p.m.’s 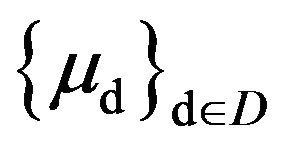 satisfies the full large deviations principle with constants
satisfies the full large deviations principle with constants  and good rate function:
and good rate function:
 (4)
(4)
Remark 1.10. The space E of Theorem 1.9 is specificnamely  (in Theorem 1.7 E is arbitrary).
(in Theorem 1.7 E is arbitrary).
Theorem 1.9 is a special case of the Theorem 1.7.
Proof. (of Theorem 1.9)
Define the map . It is easy to see (using properties of the projective limits) that
. It is easy to see (using properties of the projective limits) that
 the map
the map  i.e.
i.e.
condition ii) of Theorem 1.7 is satisfied. Then, theorem 1.9 follows from Theorem 1.7.
The motivation for this paper was to find a “unified” way of proving large deviations results. This is done by using the projective systems approach. Using this approach, and not the one of projective limits, the proofs of most of the basic results of the theory are much easier and simpler, the arguments direct. Also, we are able to prove extensions of these results to more abstract spaces, at least in the case of exchangeable sequences of r.v.’s.
2. Applications
We now give some of the basic results of the large deviations theory. Extensions of these theorems can be easier proved using projective systems.
1) Theorem 2.1. (Cramer)
Let ![]() be a sequence of independent and identically distributed (i.i.d) random variables (r.v.’s), taking values in
be a sequence of independent and identically distributed (i.i.d) random variables (r.v.’s), taking values in  with (common) distribution
with (common) distribution 
and .
.
1) If
 (5)
(5)
then: a) (upper bound)  closed:
closed:
 (6)
(6)
with

and
 (7)
(7)
b) , the set
, the set  is compact.
is compact.
2) (lower bound)  open:
open:
 (8)
(8)
Theorem 2.2 generalizes Cramer’s theorem in the case of a separable Banach space. The proof is given here using projective systems.
Theorem 2.2. (Donsker-Varadhan 1976) (Generalization of Cramer’s theorem)
Let E be a separable Banach space and F its Borel σ-algebra. Let ![]() be a sequence of i.i.d. E-valued r.v.’s and
be a sequence of i.i.d. E-valued r.v.’s and
 where
where .
.
Then, the sequence of p.m.’s  satisfies the large deviations principle with constants
satisfies the large deviations principle with constants  and good rate function Ι:
and good rate function Ι: where
where  is the dual space of Ε and
is the dual space of Ε and

(in other words Theorem 2.1. is true).
Proof.
Let  be the family of finite-dimensional subspaces of
be the family of finite-dimensional subspaces of , directed upward by inclusion. For each
, directed upward by inclusion. For each
 , let
, let  and
and
 the canonical projection of Ε onto
the canonical projection of Ε onto , i.e.
, i.e. ; for each
; for each
 , let
, let  with
with
 be the canonical projection. The family
be the canonical projection. The family  is a projective system
is a projective system
( are finite-dimensional normed spaces)
are finite-dimensional normed spaces)
and  satisfy the assumptions of Theorem 1.7, since:
satisfy the assumptions of Theorem 1.7, since:
i) The assumption implies that the sequence of p.m.’s. ![]() is exponentially tight, since:
is exponentially tight, since:

If t, a are constants, and r such that: 
 , we get
, we get .
.
For given , we choose the (compact) set:
, we choose the (compact) set:

ii) For each  the sequence of p.m.’s
the sequence of p.m.’s
 satisfies the full large deviations principle with good rate function:
satisfies the full large deviations principle with good rate function:
 .
.
In fact, since:
 If we define the r.v.’s
If we define the r.v.’s , they are i.i.d. with common distribution
, they are i.i.d. with common distribution  and values in the space
and values in the space . Also
. Also

from hypothesis, so using Cramer’s Theorem 2.1 (for finite dimensional spaces, see e.g. [1,4]), we have that the sequence of p.m.’s:

satisfies the large deviations principle with rate function
(using that ):
):

From i) and ii), and Theorem 1.7 we get that, the sequence of p.m.’s. ![]() satisfies the large deviations principle with good rate function
satisfies the large deviations principle with good rate function
 .
.
But: , so
, so

When someone deals with the empirical measures of an i.i.d sequence, the following large deviations result is true.
2) Theorem 2.3. (Sanov’s theorem in  for independent random variables)
for independent random variables)
Let ![]() be a sequence of independent and identically distributed r.v.’s, taking values in
be a sequence of independent and identically distributed r.v.’s, taking values in  with (common) distribution
with (common) distribution ,
,  the space of probability measures on
the space of probability measures on  equipped with the weak topology
equipped with the weak topology . Then:
. Then:
1) a) (upper bound)  (weakly) closed:
(weakly) closed:

with  Dirac’s measure defined on x, and
Dirac’s measure defined on x, and
 (9)
(9)
(Kullback-Leibner information number or relative entropy of ν with respect to μ)
b) , the set
, the set  is (weakly) compact.
is (weakly) compact.
2) (lower bound)  open:
open:

Remark 2.4. Theorem 2.3 is also true in the case of r.v.’s taking values in a complete separable topological space S and the space of probability measures P(S) is endowed with the weak topology (Donker-Varadhan (1976) and Bahadur-Zabell (1979) [1,5]). We prove now a generalization of Theorem 2.3 (the space P(S) is endowed with the τ-topology instead of the weak), using suitable projective systems. Also the r.v.’s are taking values on any set S which is endowed with a σ-algebra S (no need for topology on S).
Let  be a measurable space (i.e. S is any set and S a σ-algebra of subsets of S) and assume that the space
be a measurable space (i.e. S is any set and S a σ-algebra of subsets of S) and assume that the space  is endowed with the τ-topology
is endowed with the τ-topology

where  the space of the bounded, S measurable maps
the space of the bounded, S measurable maps ; convergence of nets of p.m.’s is defined in a similar way). Let also
; convergence of nets of p.m.’s is defined in a similar way). Let also be the σ-algebra induced on
be the σ-algebra induced on  by
by .
.
Theorem 2.5. (Sanov’s theorem for the τ-topology)
Let ![]() be a sequence of i.i.d. r.v.’s, with (common) distribution
be a sequence of i.i.d. r.v.’s, with (common) distribution , and values in the set S and S a σ-algebra of subsets of S. Then:
, and values in the set S and S a σ-algebra of subsets of S. Then:
1) a) (upper bound) :
:

b) , the set
, the set 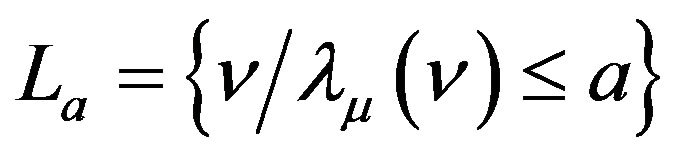 is τ-compact.
is τ-compact.
2) (lower bound) :
:

Proof.
Let  and
and  the family of all finite subsets of
the family of all finite subsets of , directed upward by inclusion. For
, directed upward by inclusion. For  is defined by:
is defined by:  and for
and for
 is the restriction map. It is easy to see that: Ι) the maps
is the restriction map. It is easy to see that: Ι) the maps  are
are  - measurable ΙΙ) the τ-topology on
- measurable ΙΙ) the τ-topology on , is the initial topology induced by the maps
, is the initial topology induced by the maps , making the family
, making the family  a projective system.
a projective system.
If  and for
and for 
the probability measure:
 where
where  with
with 
defined by ![]() and the r.v.’s
and the r.v.’s
 are i.i.d
are i.i.d  -valued and
-valued and
 .
.
Using 2.1. (for ), we get that the sequence of p.m.’s
), we get that the sequence of p.m.’s  satisfies the large deviations principle with rate function:
satisfies the large deviations principle with rate function:

i.e. condition i) of Theorem 1.7 is satisfied.
Also using an argument similar to that of Theorem 2.1 in [6], or else Lemma 2.1 [7] implies that , the set
, the set
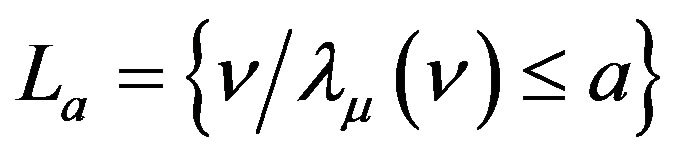 is τ-compact. This, using Lemma 2.2 [7], implies that
is τ-compact. This, using Lemma 2.2 [7], implies that

(condition ii) of Theorem 1.7). So, using Theorem 1.7, the sequence of p.m.’s ![]() satisfies the large deviations principle with rate function
satisfies the large deviations principle with rate function .
.
3) Theorem (Sanov’s theorem for exchangeable r.v.’s)
Sanov’s Theorem 2.5 is still true in the case when the independence, as a dependence relation among the random variables of a stochastic process, is replaced by a weaker one described below.
Definition 2.6. Let  be r.v.s defined on the p.s.
be r.v.s defined on the p.s.  and values in the m.s.
and values in the m.s. . We say that the r.v.’s are exchangeable or interchangeable [8], if the joint distribution of any κ of them
. We say that the r.v.’s are exchangeable or interchangeable [8], if the joint distribution of any κ of them , depends only on κ and not the specific r.v.’s. (the r.v.’s are identically distributed but not necessarily independent).
, depends only on κ and not the specific r.v.’s. (the r.v.’s are identically distributed but not necessarily independent).
The notion of exchangeability is central in Bayesian Statistics and plays a role analogous to that played by i.i.d sequences in classical frequentist theory (in B.S. an exchangeable sequence is one such that future samples behave like earlier samples, meaning that any order of a finite number of samples is equally like). The bivariate normal distribution, the classical Polya’s urn model, any convex combination of i.i.d. r.v.’s, are some examples of exchangeable r.v.’s. An i.i.d sequence is (trivially) an exchangeable one and the same is true for a mixture distribution of i.i.d. sequences. A converse proposition (to this) is the well known, powerful result in the case of exchangeable sequences, de Finetti’s theorem.
Theorem 2.7. (de Finetti’s representation theorem)
If ![]() is a sequence of exchangeable r.v.’s, then there is a probability space
is a sequence of exchangeable r.v.’s, then there is a probability space  and transition probability function
and transition probability function , i.e. a function such that:
, i.e. a function such that:
a)  is a probability measure on S b)
is a probability measure on S b)  is a measurable function on Θ, and
is a measurable function on Θ, and
 (10)
(10)
with  is the product measure on
is the product measure on  with all its components equal to
with all its components equal to . We say that, P is a mixture of the p.m.’s
. We say that, P is a mixture of the p.m.’s  with mixing measure m.
with mixing measure m.
Theorem 2.8. (Sanov’s theorem for exchangeable r.v.s in τ-topology)
Let  be a measurable space, the space
be a measurable space, the space 
is endowed with the τ-topology and .
.
Let also  and:
and:
 (11)
(11)
Let ![]() be a sequence of exchangeable r.v.’s taking values in S and suppose that the function
be a sequence of exchangeable r.v.’s taking values in S and suppose that the function
 is τ-continuous. Then:
is τ-continuous. Then:
1) If the space Θ is compact
α) (upper bound) :
:
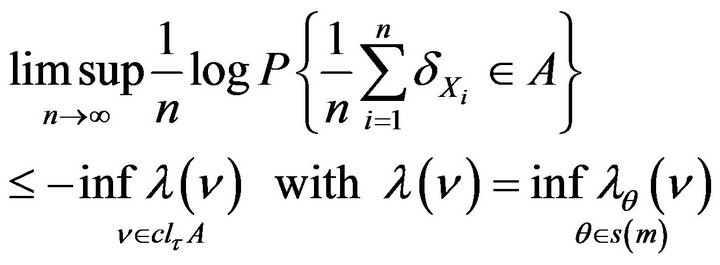
β) , the set
, the set  is τ-compact.
is τ-compact.
2) (lower bound) :
:

Proof.
Using Theorems 2.1 and 2.2 [9], it is enough to prove:
whenever , the sequence of p.m.’s
, the sequence of p.m.’s  satisfies the large deviations principle with rate function
satisfies the large deviations principle with rate function .
.
We define the projective system  where
where
 the family of all finite subsets of
the family of all finite subsets of , directed upward by inclusion,
, directed upward by inclusion,  for
for , the map
, the map  is defined by
is defined by 
and for  is the restriction map.
is the restriction map.
Finally . Then:
. Then:
Ι) For : the p.m.
: the p.m.

where 
![]() and the r.v.s
and the r.v.s  are i.i.d (with respect to the p.m.
are i.i.d (with respect to the p.m. ) with values in
) with values in . The map:
. The map:

is jointly lower-semi-continuous, so using Theorem 3.1. [9] (or directly using Gartner-Ellis theorem), we get that the sequence of p.m  satisfies the large deviations principle with rate function:
satisfies the large deviations principle with rate function:

II) It can be proved (in a way analogous to Theorem 2.1 Daras [6], see also the proof of Theorem 2.5) that

Finally, the result follows using Ι) and ΙΙ) and Theorem 1.7.
Remark 2.9.
a) Sanov’s theorem is true in a more general setting, namely when the p.m. P is a mixture of p.m.’s [6]. Then, Theorem 2.8 follows, as a corollary, using de Finetti’s theorem.
b) Theorem 2.8 extends a result of Dinwoodie and Zabell [9]. They prove their statement for a sequence
![]() of r.v.’s taking values in a Polish space S (no need here for topology on S) and the space
of r.v.’s taking values in a Polish space S (no need here for topology on S) and the space  is endowed with the weak topology (stronger than the τ-topology).
is endowed with the weak topology (stronger than the τ-topology).
4) Moderate deviations
Let ![]() be a positive real sequence such that:
be a positive real sequence such that:
 , (12)
, (12)
and ![]() a sequence of exchangeable r.v.s with distribution
a sequence of exchangeable r.v.s with distribution  and for
and for :
:
 (13)
(13)
Let  be the subspace of
be the subspace of  consisting of all those maps g, such that
consisting of all those maps g, such that . Endow the space M(S) of finite signed measures on S with the topology
. Endow the space M(S) of finite signed measures on S with the topology  generated by
generated by , i.e. the smallest topology making the maps of the form:
, i.e. the smallest topology making the maps of the form:
![]() continuous and let
continuous and let
 the σ-algebra induced on
the σ-algebra induced on 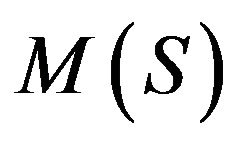 by
by . Then if
. Then if  and
and
 (14)
(14)
the following large deviations principle is true [6].
Theorem 2.10. (moderate deviations for empirical measures)
Let ![]() be a sequence of exchangeable r.v.’s taking values in S. Assume that the map
be a sequence of exchangeable r.v.’s taking values in S. Assume that the map
 is τ-continuous. Then:
is τ-continuous. Then:
1) If the space Θ is compact, then a) (upper bound) :
:
 with
with

b) , the level set
, the level set  is τ- compact.
is τ- compact.
2) (lower bound) :
:

Remark 2.11.
a) Large deviations with normalizing constants of the form (12) are being called moderate deviations [6,10].
b) Theorem 2.10 generalizes Theorem 3.1. in [11].
There, the sequence  is based on a sequence of r.v.’s taking values in a m.s.
is based on a sequence of r.v.’s taking values in a m.s.  and the space
and the space  is endowed with the τ-topology.
is endowed with the τ-topology.
c) Theorem 2.10 is true in general, namely when the p.m. P is a mixture of p.m.’s [6]. Then, Theorem 2.10 follows using de Finetti’s theorem.
REFERENCES
- A. Dembo and O. Zeitouni, “Large Deviations Techniques and Applications,” Jones and Bartlett, Boston, 1993.
- D. W. Strook, “An Introduction to the Theory of Large Deviations,” Springer-Verlag, New York, 1984. doi:10.1007/978-1-4613-8514-1
- A. de Acosta, “Exponential Tightness and Projective Systems in Large Deviation Theory,” In: D. Pollard, E. Togersen and G. Yang, Eds., Festschrift for Lucien Le Cam, Springer, New York, 1997, pp. 143-156,
- J. A. Bucklew, “Large Deviation Techniques in Decision, Simulation and Estimation,” John Wiley & Sons, New York, 1990.
- P. Dupuis and R. Ellis, “A Weak Convergence Approach to the Large Deviations,” Wiley Series in Probability, New York, 1997.
- T. Daras, “Large and Moderate Deviations for the Empirical Measures of an Exchangeable Sequence,” Statistics & Probability Letters, Vol. 36, No. 1, 1997, pp. 91- 100. doi:10.1016/S0167-7152(97)00052-7
- A. de Acosta, “On Large Deviations of Empirical Measures in the Τ-Topology,” Journal of Applied Probability, Vol. 31, 1994, pp. 41-47.
- D. J. Aldous, “Exchangeability and Related Topics. Ecole d’ Ete de Probabilites de Saint-Flour XIII 1983,” Lecture Notes in Mathematics 117, Springer, New York, 1985.
- I. H. Dinwoodie and S. L. Zabell, “Large Deviations for Exchangeable Random Vectors,” The Annals of Probability, Vol. 20, No. 3, 1992, pp. 1147-1166. doi:10.1214/aop/1176989683
- T. Daras, “Trajectories of Exchangeable Sequences: Large and Moderate Deviations Results,” Statistics & Probability Letters, Vol. 39, No. 4, 1998, pp. 289-304.
- A. de Acosta, “Projective Systems in Large Deviation Theory II: Some Applications,” Probability in Banach Spaces 9, Vol. 35, 1994, pp. 241-250.

