Received 17 March 2015; accepted 9 April 2015; published 16 April 2015

ABSTRACT

Bell’s theorem determines the number of representations of a positive integer in terms of the ternary quadratic forms 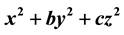with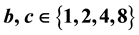. This number depends only on the number of representations of an integer as a sum of three squares. We present a modern elementary proof of Bell’s theorem that is based on three standard Ramanujan theta function identities and a set of five so-called three-square identities by Hurwitz. We use Bell’s theorem and a slight extension of it to find explicit and finite computable expressions for Tunnel’s congruent number criterion. It is known that this criterion settles the congruent number problem under the weak Birch-Swin- nerton-Dyer conjecture. Moreover, we present for the first time an unconditional proof that a square-free number 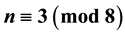is not congruent.

Keywords:

Sum of Squares, Ternary Quadratic Form, Theta Function, Hurwitz Three-Squares Formula, Congruent Number, Weak Birch-Swinnerton-Dyer Conjecture

1. Introduction

A seminal breakthrough in the theory of numbers is the determination by Gauss [1] of the number of representations 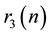of an integer n as a sum of three squares 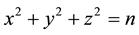counting zeros, permutations and sign changes (e.g. Dickson [2] , Preface, pp. ix, x). A very explicit modern expression for this counting function is given in Cooper and Hirschhorn [3] , Lemma 4, Equation (3.1), and Theorem 3, Equation (1.27), (1.28). Note that the latter result has only been obtained quite recently by Hirschhorn and Sellers [4] .

More generally, given a ternary (diagonal) quadratic form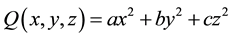, one is interested in the total number 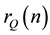of integer solutions of the Diophantine equation. This number is also

denoted by. By the time of Dickson’s monumental “History of the Theory of Numbers”, only few

specific results are known for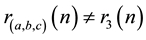. Bell [5] mentions an unproven result by Liouville and incomplete results by Torelli and Stieltjes (see Dickson [2] , pp. 294, 295, and Dickson [6] , pp. 133, 216).

Using 13 identities about theta functions, including some important ones by Kronecker and Hermite, Bell [5] determines 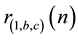for the 10 possible ternary quadratic forms with,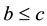. For these forms, the corresponding counting functions depend only upon. Bell’s theorem is relevant for an important con- temporary problem, namely the theorem of Tunnel [7] , which states, conditionally on the weak Birch-Swinnterton- Dyer (BSD) conjecture for elliptic curves, a necessary and sufficient condition for a number to be congruent.

The ancient but still unsolved congruent number problem has already been studied by Diophantus, the Arab scholars of the tenth century and Leonardo of Pisa (Fibonacci) (e.g. Dickson [2] , Chap. XVI, Mordell [8] , p. 71). A positive rational number is a congruent number if it is the area of some right triangle with rational sides. As shown by Koblitz [9] , Section 1.1, one can restrict the analysis to square-free natural numbers, which will be assumed throughout. It is also known that n is a congruent number if, and only if, the elliptic curve has a non-trivial rational point (for a precise constructive characterization see Hürlimann [10] , criterion (E3)). Up to the weak Birch-Swinnerton-Dyer (BSD) conjecture for the elliptic curve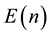, an elegant characterization of congruent numbers has been obtained by Tunnel [7] (see Koblitz [9] , Theorem, p. 221, or Cohen [11] , Theorem 6.12.4). Nowadays, it is even possible to compute large tables of congruent numbers conditionally on the validity of the weak BSD conjecture (e.g. Cohen [11] , Remark, p. 568) without using Tunnel’s theorem. Nevertheless, this exercise requires advanced mathematics and, for this reason, Tunnel’s theorem remains attractive from the viewpoint of elementary number theory. According to this result, if is a square-free and odd, respectively even, congruent number, then one has

. (1.1)

Moreover, if a weak form of the BSD conjecture holds (i.e. if the L-function of vanishes at 1, then the rank of is positive), then the converse also holds. Therefore, any computer algorithm able to verify the validity of (1.1) will produce congruent numbers under the truth of the weak BSD conjecture. Actually, Bell did a first step to make (1.1) effective by finding expressions for and that only depend upon. In the Sections 2 and 3, we improve Bell’s approach and display explicit finite and computable expressions for (1.1).

A brief description of the content follows. In Section 2, a modern elementary proof of Bell’s theorem is given. It uses only three standard theta function identities and a set of five three-square identities by Hurwitz [12] that have been revisited in Cooper and Hirschhorn [13] . Henceforth, the proof is more direct and less complex than the original derivation by Bell [5] . In Section 3, explicit expressions for the counting functions involved in (1.1) are determined and applied to the congruent number problem. In particular, an unconditional proof that is not congruent is given. Section 4 concludes with a brief description of some old and new facts about congruent numbers.

2. Ramanujan’s Theta Functions and Bell’s Theorem

We give a new elementary proof of Bell’s theorem. It uses Ramanujan’s theta functions

, (2.1)

the three basic identities

, (2.2)

, (2.3)

, (2.4)

and the following three squares identities of Hurwitz [12] (see Cooper and Hirschhorn [13] , Theorem 1, identities (1.3)-(1.4), (1.6)-(1.8))

, (2.5)

, (2.6)

, (2.7)

, (2.8)

. (2.9)

Note that (2.2)-(2.4) follow from Berndt [14] , Entry 25, p. 40. Equation (2.2) is entry 25(iv), Equation (2.3) is obtained by adding 25(i) and 25(ii), and Equation (2.4) is obtained by adding 25(v) and 25(vi).

Theorem 2.1. (Theorem of Bell). The nine counting functions, , , , are determined as follows:

Form (1,1,2)

. (2.10)

Form (1,1,4)

. (2.11)

Form (1,1,8)

(2.12)

Form (1,2,2)

(2.13)

Form (1,2,4)

(2.14)

Form (1,2,8)

(2.15)

Form (1,4,4)

. (2.16)

Form (1,4,8)

(2.17)

Form (1,8,8)

(2.18)

Proof. Recall that the generating function of (with) is determined by

. Frequent use of (2.2)-(2.9) is made without further mention. For sim-

plicity the abbreviation is used. Summation always includes all natural numbers.

Form (1,1,2). With one sees that (2.10) follows from

,.

Form (1,1,4). One has

and (2.11) is shown through the uniquely defined identifications

Form (1,1,8). A calculation shows that

which implies (2.12) through the identifications

Form (1,2,2). Similarly to the above one obtains

from which one gets (2.13) as follows:

Form (1,2,4). With successive calculation one obtains

and (2.14) follows from the identifications

Form (1,2,8). In the same manner, one gets

which implies (2.15) as follows:

Form (1,4,4). One has, and one obtains (2.16) from the identities

Form (1,4,8). Through calculation one gets

and (2.17) follows from

Form (1,8,8). A successive calculation shows that

from which one gets (2.18) through identification of

The proof of Theorem 2.1 is complete. ◊

3. Tunnel’s Congruent Number Criterion

As seen in Section 1, Tunnel’s theorem depends upon the determination of the counting functions in Equation (1.1). While and have been determined in Section 2, it remains to find expressions for and that enables the computation of (1.1). We begin with the simpler case.

3.1. Even Square-Free Congruent Numbers

The following auxiliary result in the style of Bell is required.

Lemma 3.1. Let, respectively, be the coefficient of in the -expansion of,

respectively. Then, the counting function is determined as follows:

(3.1)

Proof. We proceed similarly to the proof of Theorem 2.1. One has

from which one obtains (3.1) through the uniquely defined identifications

◊

We are ready for the following result.

Theorem 3.1. (Even square-free congruent numbers) Suppose the weak BSD conjecture holds and let n = 2m be a square-free number. Two cases can occur.

Case 1: If, then is congruent.

Case 2:

The number is congruent if, and only if, one has, where this equation is determined by the formulas

. (3.2)

Proof. Case 1 is easy. If m = 4j + 3 then by (2.17) and (3.1) one has and the result follows by (1.1) and the weak BSD conjecture. Consider now Case 2 and suppose that. Using (2.17) and (2.8) one sees that

,

where is the number of representations of as a sum of two triangular numbers. The right-hand side is a convolution sum with coefficients

.

Using that and rearranging one obtains the first formula in (3.2). The used identity between squares and triangles is part of more general similar relationships due to Bateman and Knopp [15] (see also Barrucand, Cooper and Hirschhorn [16] and Cooper and Hirschhorn [17] ). For the second formula one proceeds similarly. With Lemma 3.1 one has

, which implies

and the second formula in (3.2). ◊

Remark 3.1. The first formula in (3.2) implies some identities between squares (respectively triangles) and certain partial sums of Jacobi symbols. Indeed, alternatively to the above one has with Cooper and Hirschhorn [3] , Theorem 3, Equation (1.28), the formulas

3.2. Odd Square-Free Congruent Numbers

Again, one needs an auxiliary result.

Lemma 3.2. Let, respectively, be the coefficient of in the -expansion of

, respectively. Then, the counting function

for odd m is determined as follows:

. (3.3)

Proof. As in the proof of Theorem 2.1 one has

The first product with replaced by is the generating function of the Bell form (1,2,8) in Theorem 2.1 and contributes to the counting function for numbers divisible by 4. Similarly, the second product contributes to the counting function for numbers divisible by 2. The only contributions to for odd m stem from the third and fourth product. For these one has

Since there is no contribution to the counting function for odd numbers congruent to 5 and 7 mod 8, the Lemma is shown. ◊

Theorem 3.2. (Odd square-free congruent numbers). Suppose the weak BSD conjecture holds and let m be an odd square-free number. Three cases can occur.

Case 1: If, then m is not congruent (independently of the weak BSD conjecture).

Case 2: If, then m is congruent.

Case 3:

The number is congruent if, and only if, one has, where this equation is determined by the formulas

(3.4)

Proof. We begin with Case 2. If then by (2.15) and (3.3) one has

and the result follows by (1.1) and the weak BSD conjecture. Consider now Case 3 and suppose that. Using (2.15) and (2.7) one sees that

,

which implies the first formula in (3.4). According to Lemma 3.2 one can write

, where and are the coefficients of in the -expansions of and respectively. Therefore, one has

,

which yields the first sum in the second formula of (3.4). Similarly, one has

.

Making use of the fact that (see the proof of Theorem 3.1) one obtains the second sum in (3.4). It remains to show Case 1. Using (2.15) one has

.

On the other hand from Lemma 3.2 one knows that

.

Clearly, the theta function product is the generating function for the number of representations of in the form

,

where, with, are triangular numbers. Now, one has the following

one-to-one correspondence between solutions of and. If

, then without loss of generality and. Through permutations one can arrange that and. One sees that

,

are non-negative integers that satisfy the equations

,

hence. Taking into account permutations and sign changes one must have

. Through application of Tunnel’s theorem one sees that

,

which is strictly positive by the Gauss-Legendre theorem on the sum of three squares. Case 1 follows and the proof is complete. ◊

Remark 3.2. Similarly to Remark 3.1, the first formula in (3.4) implies the following identity (see Cooper and Hirschhorn [3] , Theorem 3, Equation (1.28))

.

4. Notes on Congruent Numbers

To conclude the present work, some comments on the obtained results might be of interest for future research in this area. In the era before Tunnel [7] , some important results were already known. For example, Genocchi proved in 1855 and 1874 that a prime and 2p with a prime were not congru- ent (see Dickson [2] , pp. 465, 467). Later on, Nagell [18] gave a very elementary proof of the fact that a prime was not congruent. Bastien [19] proved that 2p with a prime is not congruent. Heegner [20] and Birch [21] proved that 2p with a prime was congruent. Stephens [22] proved that a prime was congruent. The conjecture that is congruent is due to Alter, Kurtz and Kubota [23] and has been shown by Stephens [22] to be a corollary of the Selmer parity conjecture. After Tunnel [7] , all of the known results are more or less straightforward consequences of his famous congruent number criterion conditional on the truth of the weak BSD conjecture whenever required. For example, using elementary congruence properties Conrad [24] , Example 20, shows that if and that if. Our equally simple derivation of this statement has the advantage to follow directly from general counting formulas for the relevant ternary quadratic forms. Though Ono [25] , p. 163, mentioned that a square-free number was not congruent, we were not able to spot a reference with a proof of this result. Our unconditional result generalizes the corresponding one by Genocchi and Nagell for a prime (see also Ono [25] , Theorem 4.7, p. 162). In fact, the only non-trivial remaining situations are Case 2 in Theorem 3.1 and Case 3 in Theorem 3.2, which are settled conditionally on the weak BSD conjecture on the basis of equations (3.2) and (3.4).

References