ABSTRACT

Cancer immunotherapy aims at enhancing immune system to defend against the tumor. However, it is associated with injecting small doses of tumor-bearing molecules or even using drugs. The problem is that how to schedule these injections effectively and/or how to apply drugs in a way to decrease toxic side effects of drugs such that the tumor growth to be stopped or at least to be limited. Here, the theory of optimal control has been applied to find the optimal schedule of injections of an immunotherapeutic agent against cancer. The numerical method employed works for any dynamic linear system and has almost precise solution. In this work, it was tested for a well known model of the tumor immune system interaction.

1. Introduction

In the field of mathematical biology it is possible to describe certain phenomena by mathematical models and derive knowledge from them. Specifically, the human immune system consists of detection systems and required weapons. These systems play important roles in defending against most pathogens. Cancer immunotherapy is the use of the immune system to reject cancer. The main premise is stimulating the patient’s immune system to attack the malignant tumor cells that are responsible for the disease. This can be either through immunization of the patient (e.g., by administering a cancer vaccine, such as Dendreon’s Provenge), in which case the patient’s own immune system is trained to recognize tumor cells as targets to be destroyed, or through the administration of therapeutic antibodies as drugs, in which case the patient’s immune system is recruited to destroy tumor cells by the therapeutic antibodies. Cell based immunotherapy is another major entity of cancer immunotherapy. This involves immune cells such as the Natural killer Cells (NK cells), Lymphokine Activated killer cell (LAK), Cytotoxic T Lymphocytes (CTLs), Dendritic Cells (DC), etc., which are either activated in vivo by administering certain cytokines such as Interleukins or they are isolated, enriched and transfused to the patient to fight against cancer.

Since the immune system responds to the environmental factors it encounters on the basis of discrimination between self and non-self cells. Many kinds of tumor cells that arise as a result of the onset of cancer are more or less tolerated by the patient’s own immune system since the tumor cells are essentially the patient’s own cells that are growing, dividing and spreading without proper regulatory control.

In spite of this fact, however, many kinds of tumor cells display unusual antigens that are either inappropriate for the cell type and/or its environment, or are only normally present during the organisms’ development (e.g. fetal antigens). Other kinds of tumor cells display cell surface receptors that are rare or absent on the surfaces of healthy cells, and which are responsible for activating cellular signal transduction pathways that cause the unregulated growth and division of the tumor cell.

Immunotherapeutic treatment is a complex matter which depends on different aspects like tumor’s stage of growth and development and the health condition of the patient. Having a system of differential equations describing the tumor-immune dynamics, the problem of choosing the right time to administer the substance to stimulate the immune system is a mathematical control problem (see [1,2]).

In this work, by using one of the models describing this fact, a numerical method called Bezier control points method has been used to solve the model. By means of this method, it is possible to deal with a problem having an objective function or cost function with inequality constraints which the general case has been solved here. Although, it has to be mentioned that all constraints have to be linear according to the applied algorithm in this paper, it is possible to have nonlinear constraints. In Section 2, optimal control will be introduced. Bezier control points method will be discussed in Section 3. In Section 4, the immunotherapy model will be presented and aforementioned method will be implemented on it. In Section 5, results will be stated. Finally, Section 6 will give a conclusion briefly.

2. Optimal Control

This paper aims at minimizing quadratic cost functional over solutions of time varying systems of the form

(1)

where, , and are matrices functions and , are vectors functions, where the entries of mentioned matrices are polynomials in , is system state vector, is control vector, and .

The fixed finite terminal time is given, and is the vector of initial conditions.

One of the methods to solve optimal control problem (1), is based on parameterizing the state/control variables, which convert the problem to a finite dimensional optimization problem, i.e. a mathematical programming problem (see [3-14]).

Analytical techniques developed in [9] are of benefit also in studying the convergence properties of related algorithms for solving optimal control problems, involving Chebyshev type functional constraints where, owing to the use of a variable step size in integration or high order integration procedures, it is not either possible or inconvenient to base the analysis on a priori discretization of the dynamic. The method used slack variables to convert the inequality constraints into equality constraints.

In this paper, we show a novel strategy by using the Bezier curves to find the approximate solution for (1). In this method, we divided the time interval, into 2K subintervals and approximate the trajectory and control functions in each subinterval by Bezier curves. We have chosen the Bezier curves as piecewise polynomials of degree n, and determine Bezier curves on any subinterval by n + 1 control points. By involving a least square optimization problem, one can found the control points, then the Bezier curves that approximate the action of control and trajectory, as well.

To show the effectiveness of this method the computational results of an example is presented and compared with the results obtained in [15].

3. Bezier Control Points Method

Consider dynamical system (1). Divide the interval into a set of grid points such that

where, and k is a chosen positive integer.

Let for [11].

The optimal control problem (1) can be divided to the following suboptimal control problems:

(2)

where

and 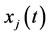and are respectively the state and control functions in. Our strategy is to divide the interval into two subintervals and then using a Bezier curve to approximate and by and respectively, where and are given below. Individual Bezier curves that are defined over the subintervals are joined together to form the Bezier spline curves. For define the Bezier polynomials of degree n that approximate the actions of and over the interval

as follows

(3)

where

are the Bernstein polynomials of degree n over the interval

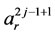, and are respectively p and m ordered vectors from the control points. By substituting (3) into the Equation (2), one may define for and, as

and where is characteristic function for.

Beside the boundary conditions, there are also continuity constraints imposed on each successive pair of Bezier segments. Since the differential equation is of first order, the continuity of the first derivative of x (or v) is required and gives

(4)

Note 1: If we consider the C¹ continuity of w, the following constraints will be added to constraints (4),

Now, we define a residual function in as follows

where is norm and M is an enough big number. Our aim is to solve the following problem over

:

(5)

Note 2: In problem (1), if be unknown, then we set.

In next section, the immunotherapy model will be introduced on which the proposed method will be implemented.

4. Immunotherapy Model

The model of Kirschner and Panetta [16] is a well known mathematical description of the tumor–immune system interaction. Despite of its simplicity, it exhibits rich dynamics that are in qualitative agreement with experimental findings. The following model was originally developed by Kirschner and Panetta [16] and modified by Burden et al. [17]. This model represents the reciprocal interactions between the effector cells;, the tumor cells;, and the concentration of Interleukin-2;. It consists of the following differential equations

(6)

(7)

(8)

where

 (see [16]).

In brief, the rate of change for the effector cell population is expressed in Equation (6); the effectors decay at rate and are stimulated by the interaction with the tumor as well as by the presence of Interleukin-2, where c models the antigenicity of the tumor. The tumor growth is logistic and is reduced by the effectors shown in the seventh equation. The eighth equation gives the rate of change for the concentration of IL-2. Interleukin-2 is produced when the effectors interact with the tumor and decays at rate. The parameter is the main factor in determining the stability properties of the effector and cancer cells appearing in (6) incorporates the therapeutic factor. The parameters units are in, except for and b whose units are volume. The function is the control describing the percentage of adoptive cellular immunotherapy given.

Using the model described above, the purpose is to design a drug schedule that eradicates the tumor level at the end of treatment as well as infusing the least dosage of drug and maintaining low tumor levels throughout the course of treatment. The problem can be formulated as an optimal control problem with the set of dynamic equations. Generally, it may be stated as:

(9)

where is a state variables vector and is a control variable bounded by. The performance index I which has to be maximized is normally given by

(10)

where is the specified final time, is the objective value of each stage and is the performance index at the end of the process. Typical optimal controls for these type of problems are bang-bang with periodical switching from to.

To define an optimal input controller, the performance index must be selected in order that the effector and the Interleukin-2 cells are maintained in an acceptable range. Also, the amount of cancerous cells is to be at minimum level during and at the end of the therapy. For this purpose, different performance indexes were studied with trial and error method. At last, in order to have minimum quantity of cancerous cells during the therapy term is taken into consideration and at the end of therapy a linear penalty is considered. A constant coefficient is approximated to be 1000 by trial and error. A quadratic term in the form of is added to the performance index to consider the effect of inputs. In addition, and are added to keep the number of effector and Interleukin-2 cells at high level. Applying all aforementioned terms, performance index is obtained as below

(11)

where is a constant and is selected to be equal to 1000, is the control variable bounded by and B is the weight factor that represents a patient’s level of acceptance of the treatment. Burden et al. [17] did not consider any terms for minimization of cancerous cells at the end of therapy, because of that, cancerous cells started growing up at the end of therapy.

In brief, we are minimizing the amount of tumor cells both during and at the end of the treatment. Also we are maximizing the amount of effector and Interleukin-2 cells. The existence of an optimal control has been studied in [17].

5. Results of the Immunotherapy Model

This algorithm has been executed on this problem with considering some different coefficients such as

.

Numerical solution results of equations for our performance index are shown in Figure 1, and control variable is shown in Figure 2. In this figure state variables including tumor cells, the effector cells and concentration of Interleukin-2 for a therapy period (350 days) are obtained. The equilibrium point in this case is unstable because the value of is smaller than critical value (540), but optimal solution of equations pushes the system to the area with smaller cancerous cells. In this work in comparison with the works done in [16-18] (see Figures 3 and 4).

6. Conclusion

In this paper, a Bezier control points method for solving optimal control problems governed by time varying dynamical systems with constraints on the states and control has been suggested. The method replaces the constrained optimal control problem by a quadratic programming one. The control point structure provides a bound on the residual function. Results show that the

proposed method is efficient and easily applicable.

REFERENCES