Applied Mathematics
Vol.10 No.10(2019), Article ID:95599,10 pages
10.4236/am.2019.1010059
Optimization in Transition between Two Dynamic Systems Governed by a Class of Weakly Singular Integro-Differential Equations
Shihchung Chiang
Department of Finance, Chung Hua University, Taiwan
Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 2, 2019; Accepted: October 7, 2019; Published: October 10, 2019
ABSTRACT
This study presents numerical methods for solving the minimum energies that satisfy typical optimal requirements in the transition between two dynamic systems where each system is governed by a different kind of weakly singular integro-differential equation. The class of weakly singular integro-differential equations originates from mathematical models in aeroelasticity. The proposed numerical methods are based on earlier reported approximation schemes for the equations of the first kind and the second kind. The main result of this study is the development of numerical techniques for determining the stability between two dynamic systems in the minimum energy sense.
Keywords:
Optimal Requirement, Transition, Weakly Singular Integro-Differential Equations, Stability

1. Introduction
The minimum energy problem and the associated optimal control problem have been investigated for more than half a century. The system constraints can be ordinary differential equations, partial differential equations, or functional differential equations. This study introduces a numerical method for finding the minimum energy to satisfy the general criterion that can be adjusted to minimize various requirements through the selection of appropriate parameters. One system constraint is the class of equations of the first kind, which originates from an aeroelasticity problem where the mathematical model consists of eight integro-differential equations [1] . In the model, the most determinate equation is a scalar weakly singular integro-differential equation of the first kind [2] [3] . Furthermore, because of the natural facts of transition between liquid water and solid ice [4] or the aviation transition between vertical take-off and horizontal flight of an unmanned aerial vehicle [5] , we were interested in the energy issue in the transition between two basically different (but related) dynamic systems. For the setting, the second dynamic system was constructed from the first system using finite derivative delay terms that included the boundary points of the considered interval. This study followed the structure of other relevant studies [6] in assuming that the forcing terms of the system are the control forces. This study is organized as follows: Section 2 presents the criteria for the optimal issues. Section 3 presents the approach for determining the minimum energy for the transition procedure. Section 4 presents the numerical results attained by choosing different parameters for various cost requirements. Section 5 presents the summary of this study.
2. The Model
Consider the class of weakly singular integro-differential equations of the first kind
(1)
with initial data
(2)
The difference operator D is defined as
(3)
where
(4)
The weighting kernel g is integrable, positive, nondecreasing, and weakly singular at . The control force is assumed to be locally integrable for . Although a more general kernel g also works, this study focused on the Abel-type kernel (i.e., , where and from the original aeroelastic model).
The initial condition is in , which is a weighted space with weight . Note that the initial value problem in Equations (1)-(2) can be written as
(5)
provided that the function
(6)
is absolutely continuous for and the function belongs to . Without a loss of generality, we assume that .
The second system is a class of weakly singular integro-differential equations of the second kind
(7)
where l is a positive integer and . The initial condition is
(8)
For the partition between systems (2) and (3), a parameter is assumed. Therefore, the combined system can be written as
(9)
with initial data
(8)
Although the proposed methods can be applied to more general cost functions, this study primarily considered the typical cost function for comparison:
(10)
and
(11)
(12)
where h is a constant of final target state, is a target function, and parameters and are nonnegative constants with a total sum of 1.
3. The Numerical Method
This procedure is proposed to discretize system (9) and the cost function (10) simultaneously to construct two corresponding linear systems with unknowns as states and controls. The space mesh points (corresponding to the s variable) are discretized as , and a new variable is defined as
(13)
System (9) can then be reformulated as a first-order hyperbolic equation
(14)
with the condition
(15)
Next, assume that the solution to Equation (8) has the form
(16)
where the basis, is given by
(17)
Namely, are piecewise linear functions. After substituting the special form of in Equation (16) into Equations (14)-(15), the governing equations for become the following:
(18)
(19)
where , for . For time t, discretization contains , for . Define , for . By assuming , for , and , and without losing generality, we assume ,,, and Equations (18)-(19) can now be written as
(20)
(21)
for ,, and .
Furthermore, we assume a uniform mesh for both space and time, and the mesh points are and . Specifically, we have ,, for some positive integers n and m. The associated differences are defined
as ,, for the time variable and ,, for the space variable. Thus, we obtain and , for , and . Setting produces the relation for , and , and deriving Equations (20)-(21) lead to the following system:
(22)
and
(23)
for , and .
After defining corresponding constants , and , Equation (23) can be written in the following simplified form:
, (24)
The connection between the solution and α’s is as follows: Because , for ,, and , it follows that , for can be obtained in the following case:
, for . (25)
For the cost function
the discretized form is:
(26)
Taking the first derivatives of with respect to , and setting them to zero yields the following equations:
(27)
where
Systems (24) with and (27) can be set up as , where the vector consists of the unknowns , and . The structure of matrix is
and vector is given by
For the cost function
the discretized form is:
(28)
Taking first derivatives of with respect to , and setting them to zero produces the following equations:
(29)
where
Systems (24) with and (29) can be set up as , where the vector consists of the unknowns , and . The structure of matrix is
and vector is given by
4. Numerical Examples
Consider examples involving ,, initial conditions , different target final state h, and different target functions . For different criteria, the combinations of constants α’s in the cost functions are changed accordingly.
For the case , the problem is the “tracking problem”.
Typical cost distribution is as the following two graphs (Figure 1 and Figure 2).
Example 1: ,
Example 2: ,
Example 3: ,
Example 4: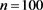 ,
, 
Example 5: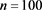 ,
, 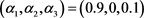
Example 6: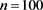 ,
, 
Figure 1. Total cost for 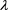 from 0 to 1.
from 0 to 1.
Figure 2. Total cost for 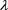 from 0 to 1.
from 0 to 1.
5. Conclusion
This study presented a numerical method for finding the minimum of the total cost when it contains two partial costs from two dynamic systems, and each cost contains three weights to adjust for different considerations of energy and different combinations of the measurable parameter 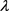 between two systems. The effectiveness of the proposed method was tested by examples. The numerical results indicated that the most stable situations are
between two systems. The effectiveness of the proposed method was tested by examples. The numerical results indicated that the most stable situations are . In other words, dynamic system with the first kind integro-differential equation is the most stable system in the minimum cost sense.
. In other words, dynamic system with the first kind integro-differential equation is the most stable system in the minimum cost sense.
Acknowledgements
Author would like to thank MOST (Ministry of Science and Technology) under grant No.108-2914-I-216-002-A1 to partially support this project.
Conflicts of Interest
The author declares no conflicts of interest regarding the publication of this paper.
Cite this paper
Chiang, S. (2019) Optimization in Transition between Two Dynamic Systems Governed by a Class of Weakly Singular Integro-Differential Equations. Applied Mathematics, 10, 826-835. https://doi.org/10.4236/am.2019.1010059
References
- 1. Burns, J.A., Cliff, E.M. and Herdman, T.L. (1983) A State-Space Model for an Aeroelastic System. Proceedings of 22nd IEEE Conference on Decision and Control, San Antonio, December 1983, 1074-1077. https://doi.org/10.1109/CDC.1983.269685
- 2. Burns, J.A., Herdman, T.L. and Stech, H.W. (1983) Linear Functional Differential Equations as Semigroups on Product Spaces. SIAM Journal on Mathematical Analysis, 14, 98-116. https://doi.org/10.1137/0514007
- 3. Kappel, F. and Zhang, K.P. (1986) Equivalence of Functional Equations of Neutral Type and Abstract Cauchy Problems. Monatshefte für Mathematik, 101, 115-133. https://doi.org/10.1007/BF01298925
- 4. Vrbka, L. and Jungwirth, P. (2006) Homogeneous Freezing of Water Starts in the Subsurface. The Journal of Physical Chemistry B, 110, 18126-18129. https://doi.org/10.1021/jp064021c
- 5. Vorsin, D. and Arogeti, S. (2017) Flight Transition Control of a Multipurpose UAV. 2017 13th IEEE International Conference on Control & Automation (ICCA), Ohrid, 3-6 July 2017, 507-512. https://doi.org/10.1109/ICCA.2017.8003112
- 6. Chiang, S.C. and Herdman, T.L. (2013) Revised Numerical Methods for Optimal Control of a Class of Singular Integro-Differential Equations. Mathematics in Engineering, Science and Aerospace, 4, 171-187.




