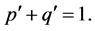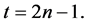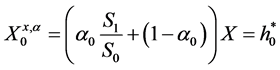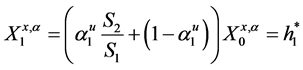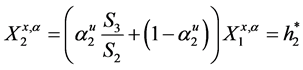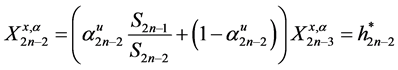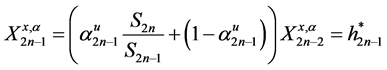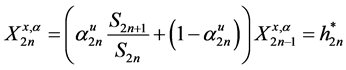Received 22 January 2016; accepted 9 May 2016; published 12 May 2016

ABSTRACT

In this paper, we considered the different strategies that generate the optimal wealth on investment. The strategy examine depends on the utility function an investor is willing to adopt, say H^* at time N in every 2n possible states; in an N period setting. Negative exponential, logarithm, square root and power utility functions were established, as the market structures changed according to a Markov chain through a martingale approach. The problem of maximization is solved via Lagrange method. The performance of the investment from day-to-day is driven by the ratio of the risk neutral probability and the probability of rising to falling.

Keywords:

Martingale, Negative Exponential, Logarithm, Square-Root, Power Utility Functions

1. Introduction

Portfolio management is a fundamental aspect in economics and finance. It is an all natural and important activity in our society for households, pension fund managers, as well as for government debt managers. The principle covers numerous and various situations of daily life. In a financial terminology, the problem of portfolio optimization of an investor trading in different assets is to choose an optimal strategy for an investment. This involves how many shares of which asset he should hold at any trading time, in order to maximize some subjective (depending on his preferences) criterion relying on his total wealth and/or consumption which in turn depends on the prices. Portfolio management is all about strengths, weaknesses, opportunities and threats in the choice of debt versus equity, domestic versus international, growth versus safety, and other trade-offs en- countered at the attempt to maximize return at a given appetite for risk. Investors need to balance the objective of maximizing the return of their investment with the constraint of minimizing the risk involved. It is generally accepted that the greater the expected return is, the greater the risk involved is.

Portfolio management (PM) guides the investor in a method of selecting the best available securities that will provide the expected rate of return for any given degree of risk and also to mitigate (reduce) the risks. Prices of assets depend crucially on their risk as investors typically demand more profit for bearing more uncertainty. Therefore, today’s price of a claim on a risky amount realized tomorrow will generally differ from its expected value. Most commonly, investors are risk-averse and today’s price is below the expectation, remunerating those who bear the risk.

Due to the high liquidity, leverage effects and their non-linear pay-off profile, together with options and other derivatives are now widely used as an investment opportunity. However, a straight forward generalization of the stochastic control approach leads to a much more complicated form of the Hamilton Jacobi Bellman equations (HJB-equations). Thus, the martingale approach of portfolio optimization deals with this problem. Hence, for any investment we have,

(1)

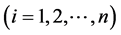
where;

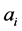= amount invested in security i.

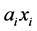= investment returns.

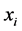= a non-negative random variable.

= the rate of return from investment i.

With payment 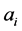returns an amount 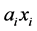after one period. The rate of return is that value 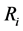that makes the present value of the return equal to the initial payment.

The traditional technique for solving dynamic programming [DP] problem stated suffers from the so-called curse of dimensionality. That is, the computational requirements of a dynamic programming problem [that needs to be solved numerically] grow exponentially in the dimensionality of the problem. One technique that applies to solving portfolio optimization problems in complete markets, is the Martingale method.

The idea behind this method is very simple: since markets can be assumed to be stable and complete, in the sense that there is no fluctuation, every contingent claim is attainable and therefore the initial price of any random variable representing a contingent claim can be computed.

In financial market where investors are facing uncertainty, the strategy that optimizes the return of an invest- ment in assets is in general not known. Suppose that the investor compares random returns whom he knowns the

probability distributions on some probability space, hence, a portfolio manager maximizes the

expected utility of his terminal wealth in a complete market with a stochastic interest rate [1] , which follows the affine dynamics [2] that allows partial risk transfer between the contributor and the fund manager [3] . L. Delong et al. [4] stated that such asset allocation strategies will be achieved only in pre-retirement accumulation phase. Thus, the optimal investment strategy follow a composite asymptotic expansion [5] . Furthermore, Eghwerido et al. [6] [7] established a case where we have negative exponential, logarithmic, square root, power utility functions with a returns on investment and their generalized form; while [8] proposed asset allocation for payment of long-term liability in a multi-period discrete time where [9] determined an equilibrium strategies for maximizing exponential utility. Korn [10] emphasized optimal investment. Also, [11] deals with investor which has the opportunity to put her wealth into derivatives with counter party risk or credit derivatives. Korn [12] considered a portfolio process yielding the highest worst-case bound where trading in the risky asset is stopped if a state process hits a predefined barrier [13] hence, mathematical theory of speculative prices through a feed back was developed elaborately [14] [15] .

The mean-variance criterion of Markowitz [16] in a one-period decision model that risk is only measured in terms of the variance of the portfolio return is criticized; that symmetric form of the variance has the undesirable side effect of not only bounding possible losses, but also possible gain [17] . Mulvey et al. [18] state that multi- stage simulation and optimization are effective for solving long-term financial planning problems. Oshorne develops the proposition that it is not absolute price changes but the logarithmic price changes which are independent of each other. [19] [20] emphasized on characterization of optimal control for diffusion processes; while Roger considered a case where an investor faced with the classical Merton problem of optimal investment in a log-Brownian asset and a fixed-interest bond, but constrained only to change portfolio. [21] [22] stressed on utility maximization in incomplete markets through semimartingale model for incomplete markets, and to characterize it via the associated dual problem. Schweizer [23] developed area of pricing and hedging contingent claims in an incomplete market by means of a quadratic criterion and [24] showed that they might be represented by an expected utility criterion.

More precisely, by denoting 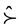the preference order on the set of random returns, we say that satisfies the criterion if and only if there exists some increasing function U from 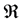into called utility function, such that

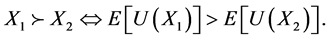(2)

The increasing property of the utility functions means that the investor prefers more wealth. Thus, the choice of the utility function allows investor the notions of risk aversion and risk premium related uncertainty, hence the strategy that delivers the optimal terminal wealth.

2. Optimal Returns with Different Utility Functions

In a financial market where investors are facing uncertainty, the return of an investment in assets is in general not known. For example, a stock yield depends on the resale price and the dividends. How to choose between several possible investments? In order to determine desirable strategies in an uncertain context, the preferences of the investor should be made explicit, and this is usually done in terms of expected utility criterion.

Negative exponential, Logarithmic, square root, power utility functions returns on investment were es- tablished [6] [7] .

Thus for negative exponential, we have

(3)

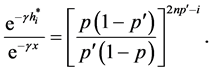
Now, suppose an investor wishes a Logarithmic rate of return, then

(4)

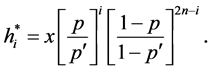
A market structure with a square root utility function with even step structure could also be,

(5)

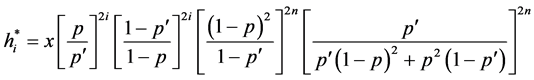
The power utility function is a generalization of the square root utility function. Thus, for an investor with power utility function return we have,

(6)

, and

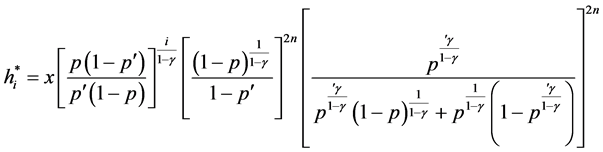
3. Model Formulation

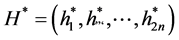
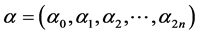
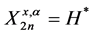
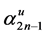
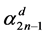
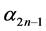
The strategy generating the optimal wealth resulted in the terminal wealth at time N in every 2n possible states. We now compute the strategy that will deliver this terminal wealth, such that. We denote the strategy by when it goes up and when it goes down; the value of the strategy decided at time

Thus, the wealth value at time t is given by

On and on to

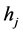
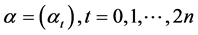
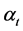
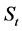
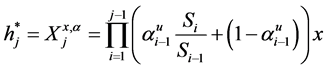
This is some sort of multiplicative effect of the wealth at time j, a function of the strategy representing the fraction of wealth invested in stock at time t with the value of chosen after observing the stock price at time t.

(7)

with,

(8)

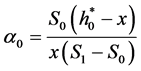
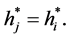
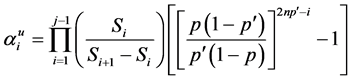
But, terminal wealth must be equivalent to optimal strategy, Hence, for a choice of negative ex- ponential, its corresponding optimal strategy is

(9)

Now, suppose an investor wishes a Logarithmic return on investment, its optimal strategy will be

(10)

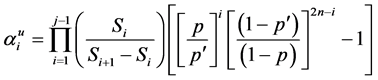
An investor with intension of a less risk investment such as the square root will have

(11)

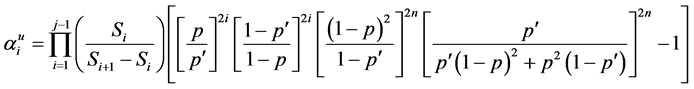
Morealso, for the power model is a generalization of the square root model, thus we have

(12)

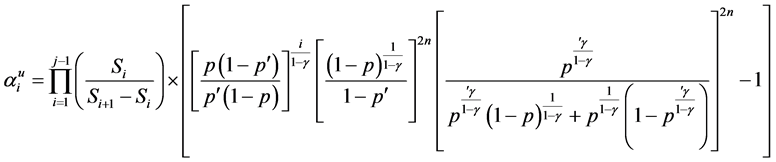
4. Concluding Remarks

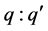
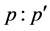
This study concludes that the optimal strategy is determined by the ratio of the probability of rising to falling as well as the ratio of the risk neutral probability measure of rising to the falling. The ROI with

different utility models showed that the Negative exponential utility model gave the best strategy of wealth which of-course, more risky.

Various strategies with different Utility functions were established. The utility functions considered are negative exponential, logarithm, square root and power utility functions. The N-step utility model results show the ratio of the utility functions at time point i in comparison with the initial starting time. The strategy with different utility models depends on the amount of risk an investor is willing to bear at each trading period. The results showed that the Negative exponential utility model gave the best strategy.

In the subsequent paper, the model will be used to predict the performances of some selected companies in the Nigeria Capital Market.

Cite this paper

J. T. Eghwerido,E. Ekuma-Okereke,E. Ekuma-Okereke,E. Efe-Eyefia,Edwin Iguodala,T. O. Obilade, (2016) Measure of Investment Optimal Strategy. Journal of Mathematical Finance,06,269-274. doi: 10.4236/jmf.2016.62023

References

NOTES

^*Corresponding author.