ABSTRACT

This paper proposes a better modified version of a well-known Multi-Objective Evolutionary Algorithm (MOEA) known as Non-dominated Sorting Genetic Algorithm-II (NSGA-II). The proposed algorithm contains a new mutation algorithm and has been applied on a bi-objective job sequencing problem. The objectives are the minimization of total weighted tardiness and the minimization of the deterioration cost. The results of the proposed algorithm have been compared with those of original NSGA-II. The comparison of the results shows that the modified NSGA-II performs better than the original NSGA-II.

1. Introduction

Job sequencing is a problem of arranging jobs in a sequence so as to minimize makespan, tardiness, completion time, waiting time, idle time and so on. The problem of job sequencing is traditional and thus quite a significant number of research studies are observed in the existing literature. In job sequencing, finding the right sequence to satisfy the above constraints for a multiple job and multiple machines is still a challenging research study. Numerous research efforts are observed towards this direction.

A variety of objectives for job sequencing problems have been investigated by the researchers in the relevant field of study and sometimes, similar set of objectives are observed in more than one research study, solving such problems with various methods. Both deterministic and non-deterministic methods have been applied to solve these types of problems. The deterministic methods include the mathematical methods like Linear Programming, Dynamic Programming, Integer Programming and so on. The non-deterministic methods mainly include various nature based algorithms like Genetic Algorithm, particle Swarm Optimization, Ant Colony Optimization, Simulated Annealing, Frog Leaping Algorithm, Bee Colony Algorithms and so on. The use of simulation techniques is also observed to solve job sequencing problems.

In this paper, a bi-objective job sequencing problem has been formulated and a modified version of NSGA-II (Non-dominated Sorting Genetic Algorithm-II) have been proposed to solve the formulated problem. The problem has also been solved by the original NSGA-II and the results of the two algorithms have been compared.

The remaining sections of this paper are organized in the following way. Section 2 reviews the existing literature; Section 3 formulates the problem; Section 4 describes the proposed modified NSGA-II; Section 5 shows results and discussion; Section 6 concludes this paper.

2. Literature Review

Job sequencing is a traditional area of research. Thus a significant number of research studies are observed in the existing literature.

The minimization of makespan (Xia and Wu [1], Xing et al. [2], Miao et al. [3]) is observed to be very common in the existing literature. Xia and Wu [1], Xing et al. [2], Li et al. [4], Zhang et al. [5], Li et al. [6], Gao et al. [7] considered total workload of machines and maximum workload as objectives. In addition to these objectives, Xia and Wu [1] and Gao et al. [7] considered minimizetion of makespan and Li et al. [4] considered maximum completion time. Rahimi-Vahed and Mirzaei [8] and Rahimi-Vahed et al. [9] worked with three objectives— minimization of total utility work, minimization of total production rate variation and minimization of total setup cost.

Tay and Ho [10] considered three objectives—minimization of makespan, mean tardiness and mean flow time. The minimization of makespan, total tardiness and total idle time was considered by Sha and Lin [11] and Mattfeld and Bierwirth [12] minimized weighted mean flow time, weighted mean tardiness, maximum tardiness and weighted number of tardy jobs. Among the other significant research studies considering tardiness, makespan and flow time as the minimization objectives include the research studies of Varadharajan and Rajendran [13], Yagmahan and Yenisey [14], Behnamian et al. [15], Chiang et al. [16].

In the work of Lian [17], the objectives considered were—minimization of runtime of every machine, earliness time and process time of jobs. Tavakkoli-Moghaddam et al. [18] considered the minimization of weighted mean completion time and weighted mean tardiness. Mazdeh et al. [19] dealt with the minimization of total job tardiness and total machine deterioration cost.

Numerous solution methodologies have been considered for solving the job sequencing problems in the existing literature. The methodologies include Linear Programming (Mazdeh et al. [19]), dynamic programming (Lewis and Slotnick [20]), Integer Programming (Baker and Keller [21]), Genetic Algorithm (Lin and Jia Zhen [22], Mattfeld and Bierwirth [12], Gao et al. [7]), Frog Leaping algorithm (Xing et al. [2], Rahimi Vahed and Mirzaei [8], Li et al. [4]), Particle Swarm Optimization (PSO) (Xia and Wu [1], Zhang et al. [5], Sha and Lin [11]), Ant Colony Optimization (ACO) (Yagmahan  and Yenisey [14], Yagmahan and Yenisey [23], Huang [24]), Simulated Annealing (SA) Lian [17], hybrid algorithms (Zhang and Wu [25], Tavakkoli-Moghaddam et al. [18], Wang et al. [26]). Besides, Moradi et al. [27] solved bi-objective job sequencing problem by NSGAII (Non-dominated Sorting Genetic Algorithm-II) [28] and NRGA (Non Ranking Genetic Algorithm) algorithms.

In this paper, the original NSGA-II has been modified by embedding a new mutation algorithm in the original NSGA-II. The existing literature shows a variety of improvements to NSGA-II, such as controlled elitism [29, 30], scalarizing fitness function [31], application of sequential quadratic programming [32], application of nearest neighbor approach [33], various sorting methods [34,35], various distribution methods [36], various diversity preservation methods [37] and so on.

A number of crossover and mutation techniques are also observed in the existing literature. Some of the common crossover techniques are One-Point Crossover, Uniform Crossover, Partially Mapped Crossover, Order Crossover, Cycle Crossover, Simulated Binary Crossover, Position Based Crossover, Parent Centric Recombination and so on. An extensive study of the literature indicates that no particular crossover or mutation technique is universally effective to all types of problems. Both the crossover and mutation algorithms depend on the type of the problem under study and the variables used in a problem.

The bi-objective job sequencing problem considered in this paper has been solved by two algorithms—NSGA-II and a modified version of NSGA-II as proposed in this paper.

3. Problem Formulation

Before formulating the problem, the assumptions and the notations are listed below.

3.1. Assumptions

Following are the assumptions made for formulating the problem:

1) Each job is processed on more than one machine;

2) Each job has a processing time and the processing times of the jobs are not same;

3) Processing time of a job varies with different machine;

4) Each machine can process only one job at a time;

5) Deterioration depends on both job and machine;

6) For each job, for each machine, there is a separate deterioration cost.

3.2. Notations

3.2.1. Decision Variables

: 1 if job j follows job i in sequence on machine m and 0 otherwise;

: 1 if job j is assigned to machine m and 0 otherwise.

3.2.2. Parameters

: Weight related to i-th job;

: Tardiness of the i-th job;

: Completion time of the i-th job;

: Due date of i-th job;

: Machine deterioration cost for job j on machine m;

J: Total number of jobs;

M: Total number of machines;

j: Subscript for jobs;

m: Subscript for machine;

: Staring time of job j on machine m;

: Processing time of job j on machine m.

3.3. Formulated Problem

(1)

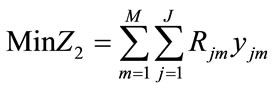(2)

Subject to the constraints:

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Objectives (1) and (2) minimize the total weighted tardiness of all jobs and the total deterioration cost of all the jobs respectively. Constraint (3) indicates that only one job precedes each job. Constraint (4) conveys that if job j follows job i then both job i and job j belong to machine m, assuming that only one job follows a job and only one job precedes a job. Constraint (5) states that each job is assigned to exactly one machine. Constraint (6) means that the completion time of job j is greater than or equal to the sum of the starting time of job j on machine m and the processing time of job j on machine m. Constraint (7) defines the tardiness. Tardiness of a job is the positive lateness of the job which is calculated by subtracting the due date from the completion of job j. Constraint (8) ensures that either job i will follow job j or job j will follow job i. Constraint (9) ensures that, and must be positive quantities.

4. Modified NSGA-II

In this paper, a modification of a popular Multi-objective Evolutionary Algorithm (MOEA) known as NSGA-II (Non-Dominated Sorting Genetic Algorithm-II) [28] is proposed. NSGA-II has been selected because of its population based nature and non-domination sort which assigns rank and crowding distance to each individual (chromosome) in the population. Besides, NSGA-II is the most widely applied MOEA as observed in the existing literature. The algorithm for the modified NSGA-II is shown in Figure 1. The algorithm continues to execute till the maximum number of generations. The main components of the algorithm are summarized below.

4.1. Initialization

The genotype of the chromosome is shown in Figure 2.

The job sequence is generated through random number generation. For each gene of the job sequence, a random number is generated and based on this random number, a job number is generated. A flag is set if a particular gene is assigned a job number. This flag prevents redundant job assignment to the genes for a particular chromosome. Next the machines are assigned to the jobs of the generated job sequence. The algorithm for the initialization is shown in Figure 3.

4.2. Non-Dominated Sorting

Before selection is performed, every individual in the population is assigned a rank based on non-domination: All non-dominated individuals are classified into one

category (with a dummy fitness value, which is proportional to the population size, to provide an equal productive potential for these individuals). The crowding distance is also calculated (see Equation (10) below) to keep a diverse front by making sure that each member stays a crowding distance apart. This keeps the population diverse and helps the algorithm to explore the fitness landscape.

(10)

where: crowding distance for individual (chromosome) I; and are the maximum and minimum objective values of the i-th objective respectively.

Non-dominated sorting is performed both after crossover and after mutation in the modified NSGA-II proposed in this paper. In case of crossover operation to be performed, the individuals are selected to form a mating pool. The selection is done through Tournament selection method. The mating pool contains the individuals on which the crossover is performed.

4.3. Crossover

Based on the structure of chromosome, order crossover has been applied in this paper. The algorithm for order crossover as applied in this paper is shown in Figure 4.

In order crossover, as applied here, two crossover sites are generated randomly and the genes in between these crossover sites are copied from one of the parents to one of the children and the same genes in the other parent, are nullified. The remaining genes in the second parent are copied to the same child, in the same order as in the second parent. In this way, one of the children is generated. The other child is generated in the same way, by exchanging parents. Figure 4 shows the generation of any one child from the parents.

4.4. Mutation

The mutation algorithm is shown in Figure 5.

The mutation is performed on the entire population. For each variable, the alleles (values of genes) representing a variable are summed up. Then the entire popu-

lation is divided into a number of divisions. The number of divisions is equal to the number of jobs in a job sequence. Then the number of individuals (chromosomes) in each division is counted and the maximum max of these counts is found out. The individuals in the division containing the maximum number of individuals are mutated to the divisions containing less number of individuals. The number of individuals mutated is the difference between max and the ideal number of individuals that should have been present in each division if the population would be divided equally into these divisions.

5. Results and Discussion

The experiments have been conducted in a PC with 2.8 GHz processor and 1 GB memory. Matlab has been used to program both the original NSGA-II and the modified NSGA-II algorithms. For each of these two algorithms, the program has been run for 10 generations starting from generation 10 to generation 100. For each of these generations, nine crossover probabilities starting from 0.1 up to 0.9 have been applied. For each of these probabilities and generations, the program has been run 10 times and the best results have been taken. Thus the total number of experiments conducted is: 10 (number of generations) × 9 (number of probabilities) × 10 (number of runs for each of these values) = 900, for each of the two algorithms.

For experimentation, a total of 6 jobs and 4 machines have been assumed. Separate deterioration cost for each job-machine pair has been considered and tardiness has been calculated based on the processing times and due dates. The population size has been taken to be 100. Based on the number of experimentations conducted, a considerable volume of results have been obtained, although it has been observed that the best results have been obtained for probabilities 0.5 to 0.9 and the results have been significant from generations 50 to generation 80. Thus the Pareto optimal solutions, in particular, are shown here for generations 50 to generation 80, for probabilities 0.5 to 0.9.

Figures 6-9 show Pareto optimal solutions for generations 50, 60, 70 and 80 respectively. The horizontal and vertical axes represent objective 1 and objective 2 respectively. Figure 6 shows nearly similar results for both the original NSGA-II and modified NSGA-II. Figure 7 shows better results for the modified NSGA-II over the original NSGA-II for all probabilities, especially for the second objective. Figure 8 shows better results on

the average, for the original NSGA-II, whereas Figure 9 shows better result for the modified NSGA-II. Thus in aggregate, Figures 6-9 show better result for the modified NSGA-II.

Tables 1-4 also show minimum values of both objective 1 and objective 2 for both the algorithms. These values have been calculated over the entire population of solutions. Tables 1 and 2 show minimum values of objective 1 for the original NSGA-II and the modified NSGAII respectively, whereas, Tables 3 and 4 show minimum values of objective 2. The comparisons of the values between Tables 1 and 2 as well as between Tables 3 and 4 show better results for the modified NSGA-II.

Tables 5 and 6 compare the execution times of the two algorithms and it is clearly observed that the values in Table 5 for the modified NSGA-II are lower (better) than the values in Table 6 (values for original NSGAII).

The figures and tables in the following parts show the performance of the two algorithms and the modified NSGA-II performs better than the original NSGA-II. The differences in terms of performance between the original NSGA-II and the modified NSGA-II, as observed from the experimental results, are summarized in Table 7. Table 7 shows that the modified NSGA-II performs better than the original NSGA-II in terms of the Pareto Optimal solutions, the minimum values of the objectives and the execution time, which in turn, indicate better search capability of the modified NSGA-II over the original NSGA-II. Thus the introduction of the mutation algorithm and the application of the mutation algorithm over the entire population are found to be effective in order to improve the overall performance of the NSGA-II algorithm, as a whole.

However the purpose of the experimentation was to observe the variety of results which have been shown by both the algorithms and this indicates that both of these algorithms can be used to solve such a job sequencing problem. However two subsets of the Pareto optimal solutions are shown in Tables 8 and 9 for the modified NSGA-II and the original NSGA-II respectively.

6. Conclusion

This paper formulates a multi-objective job sequencing problem consisting of two objectives which are minimization of total weighted tardiness and minimization of

the deterioration cost. A popular Multi-Objective Evolutionary Algorithm (MOEA) known as NSGA-II (Nondominated Sorting Genetic Algorithm-II) has also been modified in this paper. The modification includes the introduction of a mutation algorithm which has been applied over the entire population of chromosomes. The formulated problem has been solved by both the original NSGA-II and the modified NSGA-II. The results from both the algorithms have been compared and it has been observed that the modified NSGA-II shows comparatively better results than the original NSGA-II.

REFERENCES