World Journal of Condensed Matter Physics
Vol.04 No.04(2014), Article ID:51596,5 pages
10.4236/wjcmp.2014.44025
Acoustic polaron in free-standing slabs
Junhua Hou, Guangming Si
College of Physics and Information Engineering, Shanxi Normal University, Linfen, China
Email: jhhou@126.com
Academic Editor: Nikolai A. Sobolev, University of Aveiro, Portugal
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 August 2014; revised 21 September 2014; accepted 2 October 2014
ABSTRACT
The ground-state energy and its derivate of the acoustic polaron in free-standing slab are calculated by using the Huybrechts-like variational approach. The criteria for presence of the self- trapping transition of the acoustic polaron in free-standing slabs are determined qualitatively. The critical coupling constant for the discontinuous transition from a quasi-free state to a trapped state of the acoustic polaron in free-standing slabs tends to shift toward the weaker electron- phonon coupling with the increasing cutoff wave-vector. Detailed numerical results confirm that the self-trapping transition of holes is expected to occur in the free-standing slabs of wide-band- gap semi-conductors.
Keywords:
free-standing slabs, acoustic polaron, self-trapping

1. Introduction
The electron mobility is important because it is a parameter which associates microscopic electron motion with macroscopic phenomena such as current-voltage characteristics. The mobility will be changed markedly if electron state transforms from the quasi-free to the self-trapped. Moreover, many physical properties of photoelectric material are also influenced by the electron state. The self-trapping of an electron is due to its interaction with acoustic phonons. The polaron problem had also gained interest in explaining the high-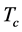 superconductors and describing the impurities of lithium atoms in Bose-Einstein ultracold quantum gases condensate of sodium atoms. Therefore the problems of acoustic polaron had been maintained interest of many scientists in the past decades [1] -[17] .
superconductors and describing the impurities of lithium atoms in Bose-Einstein ultracold quantum gases condensate of sodium atoms. Therefore the problems of acoustic polaron had been maintained interest of many scientists in the past decades [1] -[17] .
Various calculations for the ground-state energy of the acoustic polaron as a function of the e-p coupling strength have led to a discontinuous transition from a quasi-free state to a trapped state [4] - [10] . One had known that the e-p coupling effects will be substantially enhanced in confined structure, such as quasi two-dimensional (Q2D) system, so that the self-trapping transition would be easier to realize. It is meaningful to judge the possibility of the self-trapping of electron in free-standing slab systems.
It is determined in our previous works [8] that the self-trapping of the electrons in AlN as well as the holes in AlN and GaN is expected to be observed in 2D system. As a Q2D structure, the slab can be realized for most of the wide-band-gap semiconductors. Therefore the criterion for the presence of the self-trapping of electron in free-standing slab systems is desired.
In this work, a new Hamiltonian describing the deformation potential interaction between the electron and the acoustic phonon in free-standing slab systems will be derived. The self-trapping transition of the Q2D acoustic polaron will be discussed.
2. The e-LA-p Interaction Hamitonian
The interaction between the electron and the longitudinal acoustic phonon (e-LA-p) in free-standing slab is given by [13]
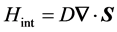 (1)
(1)
where  is the deformation potential constant, and
is the deformation potential constant, and 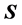 is the displacement vector of the acoustic phonon.
is the displacement vector of the acoustic phonon.
In the free-standing slab, the displacements can be taken as the form:
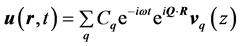 (2)
(2)
where 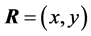 and
and 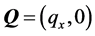 are in-plane position and phonon wave vectors, respectively,
are in-plane position and phonon wave vectors, respectively,  ,
, 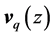 represents the
represents the 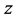 -dependence of the normal mode, and
-dependence of the normal mode, and 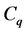 is a constant.
is a constant. 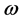 is the phonon frequency. For mixed pressure shear vertical (MPSV) modes
is the phonon frequency. For mixed pressure shear vertical (MPSV) modes 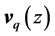 can be written as [13]
can be written as [13]
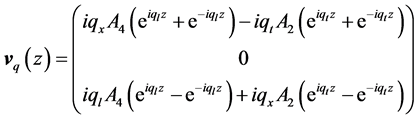 (3)
(3)
where 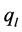 and
and 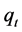 are z-components of the longitudinal and transverse phonon wave vectors. Here the constant
are z-components of the longitudinal and transverse phonon wave vectors. Here the constant 
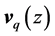




The 

Inserting Equations (3) and (4) into (5), one can obtain the following relation

where



Inserting Equations (6), (3) and (2) into (1), the e-LA-p coupling Hamiltonian is then written as

Here the e-p coupling function 

Then the e-LA-p system Hamiltonian in the free-standing slab is written as

where 

3. The Ground-State Energy
In this section, a Huybrechts-like variational approach [18] is to be used to calculate the ground-state energy of the acoustic polaron in free-standing slab.
Firstly we carry out a unitary transformation

where a is a variational parameter and will tend to 0 in the strong coupling limit and 1 in the weak coupling limit. Therefore, the Hamiltonian turns into

Then let us introduce the linear combination operators of the position and momentum of the electron by the following relations

And

where 



Inserting (12a) and (12b) into (11) and performing the second unitary transformation

The Hamiltonian finally becomes the following form:

Here we have omitted the multi-phonon processes, which contribute less to the polaronic energy.
The displacement amplitude in the second unitary transformation is determined as

by the diagonalization of the vital important part of
The ground-state energy can be calculated by averaging Hamiltonian (14) over the zero-phonon state 

By some standard treatments, the variational energy of the polaronic ground-state can be obtained as follows

The e-LA-p coupling constant is given by

In Equation (18) the variational parameters 

4. Results and discussions
The variational calculations for the ground-state energies of the acoustic polaron in free-standing slabs are numerically performed for different thickness of the slab 



As can be seen in Figure 1(a), in case of the thickness of the slab 











It is worth noting the critical values of the e-p coupling constant increase with the increasing thickness of the slab. For example, when the cutoff wave-vector 


The 





Now we use the criterion of the 


Holes have larger effective masses than electrons and must be easier to be self-trapped. For GaN, which has the light and heavy-hole masses 0.37 and 0.39 [8] respectively, the corresponding product 

Figure 1. Ground-state energies and their derivatives of the acoustic polarons in free-standing slab with the thickness L = 0.1, as functions of the e-p coupling constant α for (a) q0 = 30, (b) q0 = 60 and (c) q0 = 120, respectively.
Figure 2. Ground-state energies and their derivatives of the acoustic polarons in free-standing slab with the thickness L = 20, as functions of the e-p coupling constant α for (a) q0 = 30, (b) q0 = 60 and (c) q0 = 120, respectively.
but larger than that in slab. Therefore the light-hole in AlN can be self-trapped only in the slab with


5. Summary
The critical coupling constant for the self-trapping transition of the acoustic polarons in free-standing slab systems is determined by calculating the ground-state energies and the derivates of the acoustic polaron. The value of the criterion 

Acknowledgements
This work is supported under Grant No. 11147159 from the National Natural Science Foundation of China.
References
- Sumi, A. and Toyozawa, Y. (1973) Discontinuity in the Polaron Ground State. Journal of the Physical Society of Japan, 35, 137-145. http://journals.jps.jp/doi/abs/10.1143/JPSJ.35.137 http://dx.doi.org/10.1143/JPSJ.35.137
- Whitfield, G. and Shaw, P.B. (1976) Interaction of Electrons with Acoustic Phonons via the Deformation Potential in One Dimension. Physical Review B, 14, 3346-3355. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.14.3346 http://dx.doi.org/10.1103/PhysRevB.14.3346
- Mańka, R. and Suffczyński, M. (1980) The Large Polaron First-Order Phase Transition. Journal of Physics C: Solid State Physics, 13, 6369-6379. http://iopscience.iop.org/0022-3719/13/34/007
- Shoji, H. and Tokuda, N. (1981) Phase-Transition-Like Behavior in the Problems of Different Types of Polaron. Journal of Physics C: Solid State Physics, 14, 1231-1242. http://iopscience.iop.org/0022-3719/14/9/010 http://dx.doi.org/10.1088/0022-3719/14/9/010
- Matsuura, M. (1982) Discontinuity of the Surface Polaron. Solid State Communications, 44, 1471-1475. http://www.sciencedirect.com/science/article/pii/0038109882904586 http://dx.doi.org/10.1016/0038-1098(82)90458-6
- Peeters, F.M. and Devreese, J.T. (1985) Acoustical Polaron in Three Dimensions: The Ground-State Energy and the Self-Trapping Transition. Physical Review B, 32, 3515-3521. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.32.3515 http://dx.doi.org/10.1103/PhysRevB.32.3515
- Kirova, N. and Bussac, M.N. (2003) Self-Trapping of Electrons at the Field-Effect Junction of a Molecular Crystal. Physical Review B, 68, 235312. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.68.235312 http://dx.doi.org/10.1103/PhysRevB.68.235312
- Hou, J.H. and Liang, X.X. (2007) On the Possibility of Self Trapping Transition of Acoustic Polarons in Two Dimensions. Chinese Physics B, 16, 3059-3066. http://iopscience.iop.org/1009-1963/16/10/040 http://dx.doi.org/10.1088/1009-1963/16/10/040
- Hou, J.H. and Liang, X.X. (2007) Self-Trapping of Acoustic Polaron in One Dimension. Chinese Physics Letters, 24, 3222-3224. http://iopscience.iop.org/0256-307X/24/11/055 http://dx.doi.org/10.1088/0256-307X/24/11/055
- Khan, M.A., Shur, M.S., et al. (1995) Temperature Activated Conductance in GaN/AlGa Nheterostructure Field Effect Transistors Operating at Temperatures up to 300˚C. Applied Physics Letters, 66, 1083-1085. http://scitation.aip.org/content/aip/journal/apl/66/9/10.1063/1.113579
- Bungaro, C., Rapcewicz, K. and Bernholc, J. (2000) Ab Initio Phonon Dispersions of Wurtzite AlN, GaN, and InN. Physical Review B, 61, 6720-6725. http://journals.aps.org/prb/abstract/10.1103/PhysRevB.61.6720 http://dx.doi.org/10.1103/PhysRevB.61.6720
- Ruf, T., Serrano, J., Pavone, P., Pabst, M., Krisch, M., D’Astuto, M., et al. (2001) Phonon Dispersion Curves in Wurtzite-Structure GaN Determined by Inelastic X-Ray Scattering. Physical Review Letters, 86, 906-909. http://journals.aps.org/prl/abstract/10.1103/PhysRevLett.86.906 http://dx.doi.org/10.1103/PhysRevLett.86.906
- Hattori, J., Uno, S. N., Mori, N. and Nakazato, K. (2010) Universality in Electron-Modulated-Acoustic-Phonon Interactions in a Free-Standing Semiconductor Nanowire. Mathematical and Computer Modelling, 51, 880-887. http://dl.acm.org/citation.cfm?id=2281603
- Erdunchaolu, Xu, Q. and Liu, B.H. (2006) Effective Mass of Quasi-Two-Dimensional Strong-Coupling Magnetopolaron in Magnetic Fields. Chinese Journal of Luminescence, 27, 871-876. https://getinfo.de/app/Effective-Mass-of-Quasi-two-dimensional-Strong/id/BLSE%3ARN204645601
- Ren, B. and Xiao, J. (2007) Internal Excited State of Surface Polaron in Polyatomic Semi-Infinite Crystals. Chinese Journal of Luminescence, 28, 662-666. https://getinfo.de/app/Internal-Excited-State-of-Surface-Polaron-in-Polyatomic/id/BLSE%3ARN221707057
- Hou, J.H. and Liang, X.X. (2007) Ground State Energy and Effective Mass of Two Dimensional Acoustic Polaron. Chinese Journal of Luminescence, 28, 670-674.
- Alexandrov, A.S. and Devreese, J.T. (2009) Advances in Polaron Physics. Springer, Berlin.
- Huybrechts, W.J. (1977) Internal Excited State of the Optical Polaron. Journal of Physics C: Solid State Physics, 10, 3761-3768. http://iopscience.iop.org/0022-3719/10/19/012 http://dx.doi.org/10.1088/0022-3719/10/19/012





