Journal of Applied Mathematics and Physics
Vol.03 No.05(2015), Article ID:56756,7 pages
10.4236/jamp.2015.35070
Neutrality Criteria for Stability Analysis of Dynamical Systems through Lorentz and Rossler Model Problems
Evgeniy Perevoznikov, Olga Mikhailova
St. Petersburg State University of Trade and Economics, Petersburg, Russia
Email: eperevoznikov@yandex.ru
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 18 March 2015; accepted 24 May 2015; published 28 May 2015
ABSTRACT
Two methods of stability analysis of systems described by dynamical equations are being considered. They are based on an analysis of eigenvalues spectrum for the evolutionary matrix or the spectral equation and they allow determining the conditions of stability and instability, as well as the possibility of chaotic behavior of systems in case of a stability loss. The methods are illustrated for nonlinear Lorenz and Rössler model problems.
Keywords:
Nonlinear Dynamical Systems, Stability Analysis Methods, Dynamical Chaos, Lorenz and Rössler Model Problems

1. Introduction
The work is dedicated to the methods of practical stability analysis for systems described by nonlinear autonomous equations. The analysis of such systems is of a particular interest due to the dynamical chaos phenomena, which can be observed in cases of stability loss [1] -[3] . A stability analysis of nonlinear Lorenz and Rössler systems [1] [3] is used as an example, illustrating the possibilities of the suggested methods.
2. Stability Analysis Methods
The more common methods of system stability investigation are the spectral methods, which consist of dynamics spectrum analysis for small perturbations. The problem is defined in the following way.
Let’s assume that the system state is defined by a combination of macroscopic characteristics 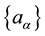 complying with the motion equations
complying with the motion equations
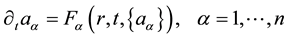 . (1)
. (1)
The linearization of these equations leads to a system of equations describing the dynamics of small perturbations 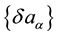 of the initial state
of the initial state 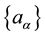
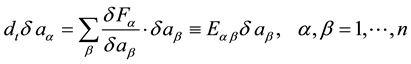 . (2)
. (2)
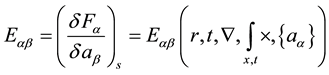
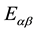 ―are the elements of the evolutionary matrix operator, which in general depend on initial state parameters, coordinates―
―are the elements of the evolutionary matrix operator, which in general depend on initial state parameters, coordinates―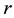 , time―
, time―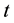 , gradients―
, gradients―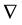 , integral operators of space and time convolution type―
, integral operators of space and time convolution type―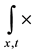 .
.
The condition of solvability of the system (2) which is its spectral equation―(SE)
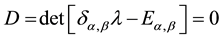 (3)
(3)
defines the eigenvalues spectrum―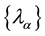 of the evolutionary operator and the stability of the initial state―
of the evolutionary operator and the stability of the initial state―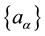 .
.
In the Fourier-Laplace transform for the perturbations in case of stationary initial states and also in cases when the initial dependences are weak in comparison with the high-speed and high-gradient perturbations (method of local dispersion relation (LDR)), the spectral equation acquires polynomial form
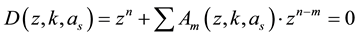 , (4)
, (4)
 ,
,

In the classical posing of the stability analysis problem, it comes down to the analysis of spectral equation roots.
The indication of an instability is the presence of a SE root with positive real part Re

Due to the fact that the exact solution of Equation (4) with complex coefficients for 
In studies [4] [5] two methods of practical stability analysis for systems described by Equation (1) are suggested. They are called-the neutrality criteria. In studies [4] [6] [7] examples of their appliance is demonstrated. The essence of these methods lies in the determination of the neutral surface―a border separating the areas of stability and instability in the parametric space―using the dynamical equations coefficients (2) or the spectral equations coefficients (4).
1) NSE (neutrality, separation, exclusion) method is based on the spectral Equation (4) and it is implemented according to the following outline
(5.1), (5.2), (5.3), (5.4)
(5.1) Neutrality―the condition of the real part of SE roots being equal to zero;
(5.2) The separation of the spectral equation into two if the neutrality condition is fulfilled;
(5.3) The exclusion of frequency or one of the parameters from the equations and obtaining of a neutral surface―

(5.4) Indication of stability and instability areas in relation to the neutral surface.
The NSE outline is fully realized for the polynomial SE. The general neutrality conditions (3.3) in this case are given by




Specifically for a third order system the conditions (6) are
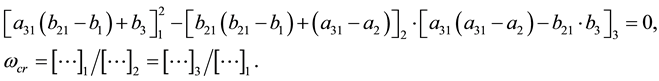
2) The


which consists of the evolutionary matrix 




The neutrality criterion and the equation for the critical frequencies in this method have the following form

The commutation of 



3. Nonlinear Systems
Assuming that Equation (1), which describe the system that is being analyzed in terms of stability, represent a combination of nonlinear autonomic equations

The perturbation dynamics of system (10) in this case are described by Equation (11)




If all the time derivatives in (11) are negative, the perturbations attenuate and the system is Lyapunov stable. If there is at least one positive derivative, the solution curves scatter; the system is not stable. The correlation of derivative signs allows to determine the possibility of chaotic behavior and the formation of complex localized structures―strange attractors [3] (see Figure 1 and Figure 2) in the phase space.
In these cases, the spectral equation method (4) and NSE method (5) for the stability analysis in their classical forms are not applicable.
Due to the fact that the 




Specifically, the criterion (12) being equal to zero corresponds to the presence of zero-order derivatives (eigen- values), the criterion sign change-corresponds to a sign change of time derivatives in dynamical Equation (11). As a result, the multiplication factor analysis in (12) represents an analysis of evolutionary matrix eigenvalues spectrum for a nonlinear system and therefore, an analysis of time derivatives signs in Equation (11).
Such generalization can technically be conducted for the NSE (5) and spectral Equation (4) methods, but in that case


So now we will use the generalized NSE and 
4. Lorenz Model Problem [1] [3]
The Lorenz problem is of a particular interest because nonlinear equations of Lorenz model result from the dynamics equations of a whole range of physical systems: The convection inside a fluid layer heated from underneath, a single-mode laser, water-wheel and other. Besides that, it demonstrates the formation of chaotic dyna- mics (Figure 1).


The Lorenz model equations have the following form
Figure 1. Lorenz attractor for “classical” values of parameters σ = 10, b = 8/3, r = 28.






In the phase space of variables 


If 

i.e. the Lorenz system is dissipative.
The system (13) has two stationary solutions-stationary states


The linearization of system (13) in relation to a solution

The spectral equation and its coefficients in a stationary case are


(It should be noted that the dissipation condition coincides in absolute value with the first coefficient of the spectral equation and is equal to the sum of eigenvalues of the evolutionary matrix. It may be shown that there is a common result.)
The NSE method for SE (17) produces two critical-neutral modes
1)
2)
The mode (18) occurs for the first stationary state and corresponds to its instability when

The mode (19) occurs for the second stationary state and for the classical values of Lorenz parameters the critical values of frequency and the parameter 

When 


The 


As could be expected, the criterion (22) shows an instability of the first stationary state (15) when





The dynamical mode is correspondingly
1) A stable point;
2) A boundary cycle;
3) An attractor (of chaotic dynamics).
This way, in the Lorenz system with 


It should be noted that the criterion (23) includes the first critical mode 
5. Rössler Model Problem
A nonlinear problem which has an evidentially expressed field of chaotic behavior with an attractor presented in Figure 2, see [1] [3] .
The Rössler model equations have the following form










From (26) it follows that the Rössler system is dissipative only in a limited field (Figure 2).
The system (25) has two stationary solutions-stationary states
Figure 2. Rössler attractor when


which are possible under the condition



The linearization of Equation (25) in relation to the solution

The spectral equation of the system (25) and its coefficients for the stationary states are correspondingly


The NSE criterion for SE (30) produces two critical-neutral modes (18, 19), which in this case take the following form

The analysis of conditions (31) combined with stationary conditions (27) shows that when 

The first critical mode occurs only for the second stationary state



The second critical mode occurs for the first stationary state, which is also unstable when


This way both stationary states are unstable in different ways.
The L-criterion (12) regarding arbitrary solutions 

For stationary solutions (27) the criterion (35) is rearranged into

As one would expect, the 


which indicates a chaotic behavior of the system with a phase portrait of the type illustrated in Figure 2.
6. Conclusion
In conclusion, the use of modified NSE methods and the 
References
- Landa, I.P. (1997) Nonlinear Waves and Oscillations. Nauka, Moscow, 496 p.
- Feigenbaum, M. (1983) Versality in Nonlinear Systems Behavior. UFN, 14, 342-374.
- Kuznetsov, S.P. (2006) Dynamical Chaos, FM. M. Ppysmatgis, Moscow, 355 p.
- Perevoznikov, E.N. and Skvortsov, G.E. (2010) Dynamics of Perturbations and Analysis of Nonequilibrium Systems Stability. SPbTEI, St-Petersburg, 139 p.
- Perevoznikov, E.N. (2006) News of Higher Educational Institutions. Physics, 10, 34-39.
- Perevoznikov, E.N. (2013) Stability Criterion for Nonlinear Systems. Springer Science, Business Media, New York.
- Perevoznikov, E.N. (2013) Short-Wave Charge Instability of Weakly Ionized Plazma Flows. IF Journal, 86, 11-16.













