ABSTRACT

The review is devoted to introduce the recent development of the study in mathematical theory and methods of mechanics of quasicrystals, respectively. The mechanics of quasicrystalline materials includes elasticity, plasticity, defects, dynamics, fracture etc. In the article some relevant measured data are collected for some important quasicrystal systems, which are necessary for understanding physics and applications of the materials. It is very interesting that the mathematical theory and solving methods of the mechanics of quasicrystals have developed rapidly in recent years, which is strongly supported by the experiments and applications. The theoretical development strongly enhances the understanding in-depth the physics including mechanics of the materials. The mathematical theory and computational methods provide a basis to the applications of quasicrystals as functional and structural materials in practice as well. More recently the quasicrystals in soft matter are observed, which challenge the study of based on the quasicrystals of binary and ternary alloys and greatly enlarge the scope of the materials and have aroused a great deal attention of researchers, an introduction about this new phase and its mathematical theory is also given in the review.

1. Introduction

An icosahedral structure in Al-Mn alloy with five-fold rotation symmetry was first discovered in April 1982, and reported in November 1984, refer to [1] and Figure 1. Immediately after the work, reference [2] claimed that the structure is a quasicrystal, which presents quasiperiodic translational symmetry and orientational symmetry that is not allowed by the well-known crystal symmetry law. This has aroused a great attention of scientists in chemistry, crystallography, physics, mathematics, materials science etc. Soon after, Chinese materials scientists [3,4] observed the five-fold symmetry and icosahedral quasicrystals in Ni-V and Ni-Ti alloys, and others found the quasicrystals with eight-, tenand twelve-fold symmetries.

The above quasicrystals are observed in binary and ternary metallic alloys, which can be called solid quasicrystals. Recently in polymers, nanoparticle mixture and colloids the quasicrystals with twelve-fold and eighteenfold symmetries are found too, which can be named soft matter quasicrystals.

In various metallic alloys, many of the quasicrystals observed so far present thermodynamically stability, they become a new class of functional and structural materials, and present current and potential applications. For the purpose of application, the chemical, physical and mechanical properties of the material have been extensively studied. In the mechanical behaviour of quasicrystals, elasticity and defects belong to the fundamentals, this review paper is focused on the subject, but some relevant topics are also discussed.

Quasicrystals include three classes, i.e., one-, twoand three-dimensional ones. For one-dimensional quasicrystals, the atom arrangement is quasiperiodic along one direction, while periodic along the plane perpendicular to it. For two-dimensional quasicrystals, the atom arrangement is periodic along one direction, while quasiperiodic along the plane perpendicular to it. For three-dimensional quasicrystals, along all three directions the atom arrangement is quasiperiodic. Within each class, there are some subclasses, which present different mechanical behaviour each other. In this paper some common features of the material and general principles of physical and mathematical theories will be introduced first, and the mathematical solutions have to be discussed only for individual classes.

The unusual structures of quasicrystals lead to some novel phenomena different from those of crystals and conventional structural materials, we have to provide some additional knowledge before the subsequent presentation.

2. Introducing Higher Dimensional Space

The discovery of quasicrystals is obtained through the diffraction patterns of electronic microscopy. Due to the special atom arrangement of quasicrystals, their diffracttion patterns cannot be described in terms of the traditional Miller index used in crystallography, instead people must take six index (n₁, n₂, n₃, n₄, n₅, n₆).The fact indicates that we must introduce higher (six) dimensional space. This is just identical to group theory. According to the group theory, a three-dimensional quasicrystal is a projection of a “periodic crystals” at sixdimensional space into three-dimensional space. Similarly, a two-dimensional quasicrystal is a projection of a “periodic crystals” at five-dimensional space into threedimensional space, a one-dimensional quasicrystal is a projection of a “periodic crystals” at four-dimensional space into three-dimensional space. So that the threedimensional physical space is a subspace of the six-dimensional space, named parallel space, denoted by. Another subspace is the complement space, or perpendicular space, marked by.Such that

(2-1)

in which notation represents direct sum.

Conventional crystals are studied in physical space, people commonly use two classes of lattice, one is taken the frame of crystal base vector, the other is so-called reciprocal vector. Between base vector and reciprocal vector there is simple algebraic relationship, which will not be concerned here. Quasicrystals are studied in space, the relevant base vector and reciprocal space are six-dimensional.

3. Principle of Symmetry Breaking of Landau-Anderson, Elementary Excitations (Quasiparticles), Phonons and Phasons

Immediately after the discovery of quasicrystals, the study on the mechanical behaviour of the material has been put forward. This is the one of advanced areas of quasicrystal study so far. Among the mechanical properties, elasticity and defects play basic and central roles.

Applying the symmetry breaking principle [5] to crystals, the symmetry is broken relative to fluid. According to the theory, the symmetry breaking leads to appearance of new elementary excitations (or quasiparticles). For crystals, the elementary excitation is phonon. An application of the symmetry breaking principle to crystal [6] gave a profound explanation to the phonon, that is the order parameter of the Landau theory on the second phase transition to be taken the density for the present case, and it can be expanded by the Fourier series in reciprocal space

(3-1)

where is the reciprocal lattice, the wave amplitude, the phase angle. Because is real, and, further putting

(3-2)

in which is just the phonon vector.

Under the longwave length approximation, may be understood as displacements of particles (atoms, molecules and irons at lattices), this is identical to that of macroscopic continuum mechanic. However the Equation (3-2) has more profound sense, which holds beyond the longwave length regime. We can understand that the phonon is as the quanta of lattice wave. The phonon is a concept that introduced in the study on lattice specific heat at low temperature by [7-9], that considered that the energy of lattice wave is quantized, the quanta is the phonon. (This is similar to the concept of photon which was introduced by Planck in study on radiation phenomena). We realize that phonon and other quasiparticles belong to a concept in the quantum methodology of condensed matter physics for describing the collective excitation of massive particles, the quasiparticles cannot be equal to the single atom or single molecule.

The physical and mathematical theories for studying quasicrystals have been existed in 1980s. At first the theory of Landau symmetry breaking is matured. The theory of incommensurate phase was developed since 1960s [10], the phason concept in quasicrystals is drawn from the theory. In the area of discrete geometry the Penrose tiling [11] created in 1974, which is one of the geometrical tools of quasicrystals. The most important algebraic tool for quasicrystals-group theory and group representation theory are matured too in that time.

By using the above theories, studies [12-18] promptly put forward the theory of elasticity of quasicrystals. Extending the point of view of on crystals, researchers gave the expression of the density of quasicrystals as

(3-3)

The form of (3.3) is similar to that of (3.1), but G here is the reciprocal vector in six-dimensional space, the reciprocal lattice in six-dimensional space, and a complex number

(3-4)

with amplitude and phase angle. Because is real, and. It seems that the formulas are similar to those of crystals given by Anderson, but the objective now studied is quasicrystalsthere exist reciprocal vectors with number. Each, can be written as, in which is integer. Further, here represents number of vectors of the mutual incommensurate -dimensional quasicrystal, in general. In the case the Anderson formula (3-2) is extended as

(3-5)

in which is understood as that (the phonon degree of freedom) in conventional crystals, while can be understood the phason degree of freedom, a newly physical quantity, which describe the local rearrangement of Penrose tiling. In (3-5), is the reciprocal vector in, whereas is the conjugated vector of in.

The hypothesis of Bak and Lubensky et al are supported by other researchers [19-24] etc, and examined by experiments, so it becomes a theory widely acknowledged.

4. Physical Basis of Elasticity of Quasicrystals

After the discovery of quasicrystals, their mechanical behaviour has been well studied. Among the field, elasticity and defects present fundamental importance, which are basic and play a core role.

Under longwave length approximation, the total displacement field can be expressed as follows

(4-1)

For both phonons and phasons, they are only the functions of radius vector in parallel space, i.e.

About this there is a theorem, but the detail is omitted here. For simplicity, the superscript in is removed in the subsequent discussion.

From (4-1) it follows two strain tensors as following:

(4-2)

where the first one is the phonon strain tensor, symmetric, the second one represents the phason strain tensor, asymmetric (Here we mention that (4-2) doesn’t hold for a class of quasicrystals-the three-dimensional cubic quasicrystals, see for detail in [43,44]). The stress tensor associated to the phonon strain tensor is denoted by, and one associated to the phason strain tensor is denoted by. The momentum conservation law yields

(4-3)

where represents body force (per unit volume), the generalized body force. One has the stress boundary conditions:

(4-4-1)

denotes traction, the generalized traction, respectively. At the boundary part given displacements there are the displacement boundary conditions:

(4-4-2)

where represents the boundary part at which the tractions are given, the boundary part at which the displacements are prescribed.

Employing the angular momentum conservation law to the phonon field we have

It follows that

(4-5)

Since and belong to different irreducible representation of point groups, from the angular momentum conservation law one cannot obtain a similar results to (4-5) for. So that

(4-6)

This means the phason stress tensor is asymmetry (This is not valid for three-dimensional cubic quasicrystals, refer to [43,44]).

Apart from two-dimensional dodecagonal quasicrystals, phonon field and phason field are in coupled, this leads to the complex stress-strain relations, the generalized Hooke’s law is:

(4-7)

in which F denotes the strain energy density (according to the physical terminology, it is called free energy), the phonon elastic constant tensor, the phason elastic constant tensor, the phonon-phason coupling elastic constant tensor, respectively. The one-dimensional quasicrystals, due to their low symmetry, the number of elastic constants is greater. The two-dimensional quasicrystals have less elastic constants than those of one-dimensional quasicrystals. The three-dimensional icosahedral quasicrystals present higher symmetry, the number of their elastic constants is only five.

The Hooke’s law can be expressed by matrix, i.e., put

(4-8)

to represent the matrix of phonon elastic constants, whereas

(4-9)

represents the matrix of phason elastic constants, and

(4-10)

represents the matrix of phonon-phason coupling elastic constants, and

(4-11)

Furthermore

(4-12)

So that the strain energy density is

(4-13)

The matrix of generalized Hooke’s law has its matrix expression

(4-14)

in which the vector with 18 components denoting the strain elements is as follows

(4-15)

The vector expression of stress elements is similar to (4-15), and

(4-16)

The above physical framework is summarized by work [25] first.

The generalized Hooke’s law (4-7) or (4-14) is a base of elastic analysis of quasicrystals, in which the determination of all independent nonzero elastic constants is a key. The application of point group theory [26] gave a important result on this problem, furthermore it is solved thoroughly in some extent for the quasicrystal systems observed to date in binary and ternary alloys in terms of group representation theory [27,28].

5. Measurements of Elastic Constants and Results

We just mentioned that one of key is the determination of all independent nonzero elastic constants, but the measurement of these constants is also important.

Among over 200 individual quasicrystals there are almost 100 icosahedral ones. No doubt that icosahedral quasicrystals belong to the most important one in the material. The nonzero independent phonon elastic constants are only two, i.e., , the nonzero independent phason elastic constants are also two, i.e., , and the phonon-phason coupling elastic constant only one, denoted by.Through neutron scattering, X-ray diffraction, nuclear-magnetic resonant, etc, one measured some elastic constants of icosahedral quasicrystals, the results are listed in Tables 1-3.

Apart from icosahedral quasicrystals, there are over 70 decagonal quasicrystals have been observed, they are also important for which there are five independent nonzero phonon elastic constants (simplified from the tensor of fourth rank), which are listed by Table 4. where denotes the bulk elastic modulus, the shear modulus, they and have unit of GPa, and the Poisson ratio.

For two-dimensional quasicrystals with ten-fold sym-

metry there are two nonzero independent phason elastic constants (simplified from the tensor of fourth rank), their experimental measured values are listed by Table 5.

For two-dimensional quasicrystals with ten-fold symmetry there are two nonzero independent phonon-phason coupling elastic constants (simplified from the tensor of fourth rank), their experimental measured values are listed by Table 6.

Recent years, the measurement technique has made a great progress. Due to the great difficulty, the measured results are still less. This is a field needed to be improved.

6. Simplification of Elasticity Equations of Quasicrystals, Displacement Potentials and Stress Potentials

Through the introducing in Section 4, one can find that: there are 22 field variables and 22 field Equations for one-dimensional quasicrystals, there are 29 field variables and 29 field Equations for two-dimensional quasicrystals, there are 36 field variables and 36 field Equations for three-dimensional icosahedral quasicrystals. The difficulty for solving is not only the huge number of field Equations, but also the asymmetry and the complexity of boundary conditions.

People are interested in the exact solutions indeed. The group of ours focus on the exact analytic solutions for different quasicrystal systems, especially for the most important icosahedral and decagonal quasicrystals. In these respects we carry out systematic study and obtain quite rich results.

The hints of the theory of classical elasticity and mathematical physics [41,42], the eliminating element method can help one to reduce the number of unknown functions, and arrive in simplification of the problems. For this purpose we need to introduce some displacement potentials or stress potentials. This procedure will be introduced according to the order from oneto threedimensional quasicrystals.

6.1. The Space Elasticity of One-Dimensional Hexagonal Quasicrystals

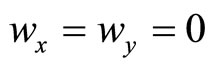For this quasicrystal system, phonon displacements are, phason displacement is (because of), the corresponding strain components

(6.1-1)

(6.1-2)

and other. The strain components are nine at all. Equations (6.1-1) and (6.1-2) are valid for all one-dimensional quasicrystals.

If we write (6.1-1) and (6.1-2) as a vector with 9 components, i.e.,

(6.1-3)

or

(6.1-4)

the corresponding vector consists of stresses

(6.1-5)

then the elastic constant matrix is as follows

in which the four indexes of phonon elastic constants are simplified to two indices, i.e., indices

so that can be denoted by:

This indicates that the number of independent phonon elastic constants is five. Second, the phason elastic constants, i.e., the independent phason elastic constants are only two. The phonon-phason coupling elastic constants

this shows the number of independent phonon-phason coupling elastic constants is three, from the elastic constant matrix, the expression of the generalized Hooke’s law is

(6.1-6)

and other.

The stress components are satisfied the following equilibrium Equations:

(6.1-7)

Eliminating the stress and strain components from (6.1-1), (6.1-6) and (6.1-7) yields the equilibrium Equations expressed by the displacement components:

(6.1-8)

The Equation set (6.1-8) is simpler than those consist of 22 Equations (6.1-1), (6.1-6) and (6.1-7), but we can further simplify (6.1-8).For the purpose one can introduce 4displacement potentials

(6.1-9)

if

(6.1-10)

(6.1-11)

then Equations (6.1-8) are satisfied, in which and are defined by:

(6.1-12)

The Equations (6.1-10) are final governing Equations, whose solving is much simpler than that of the 22 Equations given by (6.1-1), (6.1-6) and (6.1-7).Some detail can be found in [43-45]. The classical transverse isotropic elasticity is as one of special example of the present problem, i.e., the case without phason field and phonon-phason coupling field.

6.2. Other Elasticity Problems of One-Dimensional Quasicrystals

Due to the space limitation, there is no possibility to discuss every system of one-dimensional quasicrystals. For more complicated systems of one-dimensional quasicrystals, by using a decomposition and superposition procedure, problems can be simplified in some extent. Assume that axis represents the quasiperiodic arrangement direction, if put

(6.2-1)

the problem is decomposed a plane elasticity and an anti-plane elasticity problems to treat, the solving is greatly simplified. After the solving, superposing the solutions of plane elasticity and anti-plane elasticity gives an approximate description of space elasticity. The detail is not discussed any more, one can refer to [44,46]

for the detail.

The work of one-dimensional quasicrystals given in work [47-49].The decomposition and superposition procedure developed here is useful to treat elasticity of towand three-dimensional quasicrystals, some of them will be discussed in the following sections.

6.3. Two-Dimensional Quasicrystals with Fiveand Ten-Fold Symmetries

The elasticity of two-diemsional quasicrystals has 29 filed variables and 29 field Equations, is more complicated than that of one-diemsional ones. Decomposition and superposition procedure make the problems to be greatly simplified, and many results are achieved, refer to [50-55].

The five-fold symmetry quasicrystals of point group 5 m, and ten-fold symmetry quasicrystals of point group 10 mm are kinds of one with important sense in theoretical and experimental study (Their diffraction pattern and Penrose tiling are shown in Figure 2), their plane elasticity has the same characters. However the quasicrystals of point groups and are different from those of point groups 5 m and 10 mm. In the following we discuss the elasticity only for point groups 5 m and 10 mm quasicrystals and the simplification of their elasticity Equations.

Assume that the 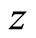axis to be the direction along which the atom arrangement is periodic. Put

(6.3-1)

then the plane elasticity has the following Equations, i.e., the Equations of deformation geometry

(6.3-2)

(6.3-3)

and the equilibrium Equations

(6.3-4)

The plane elasticity consists of 21 Equations, which can be reduced into 4 Equations by eliminating strain and stress components

(6.3-5)

where

The Equations (6.3-5) can be simplified further. By introducing new unknown functions and Ψ(x,y) such as

(6.3-6)

where, then (6.3-5) are reduced to

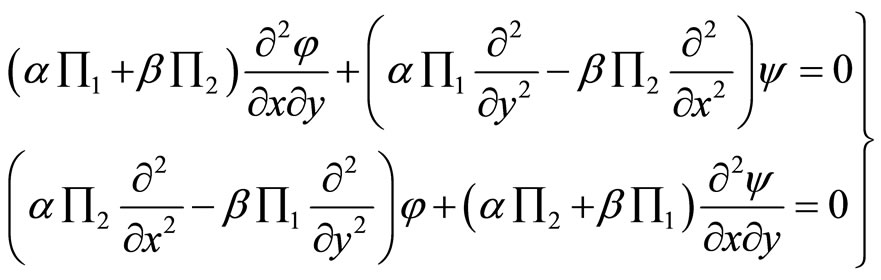(6.3-7)

here

(6.3-8)

(6.3-9)

Furthermore the functions and are expressed by

(6.3-10)

in which, and may be any function, we call it be the displacement potential, if

(6.3-11)

then (6.3-7) are satisfied. The Equation (6.3-11) is the final governing Equation of plane elasticity of quasicrystals of point groups 5 m and 10 mm. Although point groupsand quasicrystals are different from those of point groups 5 m and 10 mm, the former is more complex, the derivation shows that the final governing Equation of the latter has the same form as that of (6.3-11). In the subsequent presentation, Equation (6.3-11) will appear more times shows the Equation presents universal sense.

Under the assumption (6.3-1), the anti-plane elasticity is described by the final governing Equation

(6.3-12)

If we didn’t use displacement potential, while use the stress potential, then the plane elasticity of above certain quasicrystals can be reduced to

(6.3-13)

This shows again the importance and universality of the quadruple harmonic Equation, these work has been done by the Ref [50], in which a systematical solving for some boundary value problems of the Equation is also discussed.

6.4. Quasicrystals of Eight-Fold Symmetry of Two-Dimension

We here consider only the point group 8 mm octagonal quasicrystals(whose Penrose tiling is shown in Figure 3), and the assumption (6.3-1) is still taken. After a long derivation we find the final governing Equation of the plane elasticity

(6.4-1)

where

(6.4-2)

(6.4-3)

(6.4-4)

is the phonon-phason coupling elastic constant, refer to [50].

6.5. Two-Dimensional Quasicrystals of Twelve-Fold Symmetry (Dodecagonal Quasicrystals)

The electronic microscopic diffraction pattern and the Penrose tiling are depicted by Figure 4. It elasticity is relatively simpler, but the structure is very important, because it is observed not only in solids, but also in soft matter (polymers, nanoparticle mixtures and colloids), the latter will be discussed in Section 14.

For this kind of quasicrystals, the phonon and phason do not couple, so the coupling constant is vanish, i.e.,

(6.5-1)

Under the assumption (6.3-1), the final governing Equations are reduced to

(6.5-2)

the first one is the Equation of phonon elasticity, the second one is the Equation of phason elasticity. The detail can be found in [43,44,50].

6.6. Three-Dimensional Icosahedral Quasicrystals

Icosahedral quasicrystals belong to the most important class of the material, which are three-dimensional ones. The Figure 5 shows an outlook of the structure, whose patterns of diffraction and stereographic configuration are depicted in Figure 1, in which there are five-, two- and three-fold symmetry axes.

The elasticity consists of 36 field variables and 36 field Equations, the solving is most difficult compared with those of other quasicrystal systems.

The general Equations (4-2), (4-3) and (4-7) hold for icosahedral quasicrystals, the difference lies in the stress-stain relation, in which instead

(6.6-1)

whereand 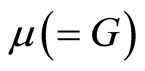are the Lamé constants. The strain and stress components with 18 components can be ordered as a vector such as, respectively

(6.6-2)

(6.6-3)

then the phason elastic constant matrix and phononphason coupling elastic constant matrix are as follows

(6.6-4)

Further the explicit expression of the constitutive Equation is given below

(6.6-4)

where.

Substituting (4-2) into (6.6-4) then into (4-7), the equilibrium Equations expressed by the displacements where

The direct analytically solving Equation set (6.6-5) is difficult very much. In the following we give some simplifications.

Assume that the axis represents the direction of five-fold direction and put

(6.5-6)

then the 36 Equations are reduced to 32 Equations, the corresponding final equilibrium Equations (6.6-5) are simplified as

(6.6-5)

(6.6-7)

where

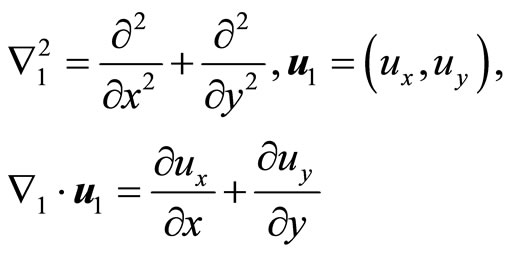
In this case the Equation set (6.6-7) is considerable simplified compared to that of (6.6-5), but which is needed to be simplified further. For this purpose we introduce a displacement potential function such as

 Then Equation set (6.6-7) is reduced to the sextuple harmonic Equation with 12 order as below

(6.6-9)

The Equation was first observed by paper [56] in 2005.

If we didn’t use the displacement potential while use the stress potential, then the final governing Equation is also a sextuple harmonic Equation with 12 order [57]

(6.6-10)

i.e., the sextuple harmonic Equation is discovered again. This shows the Equation presents its universality and importance in science and engineering.

In the work studying elasticity of three-dimensional qusicrystals we find other partial differential Equations of higher order, which are unable to list due the space limitation.

7. Analytic Solutions of Boundary Value Problems of Quasicrystals-Fourier Analysis

Historically the first solution of elasticity of quasiscrystal was given by paper [58] in 1987, in an alternative method was used for getting the solution. However one cannot find the development of the method. Afterward papers [59-61] developed the Fourier transform and Green function method, the researchers obtained some dislocation solutions by directly solving the Equations (6.3-5). These works are meaningful, of course. However we need to develop more systematical and direct methods, certain constructive methods. The simplification of governing Equations, reducing Equations with huge number to a single or few of partial differential Equations of higher order, provides a possibility to develop the constructive methods. In this respect, the Chinese scientists pay a great effort and obtain some systematical analytic solutions for complicated boundary value problems. In the following we will give some examples of solving, the practice shows that the Fourier analysis is a fundamental method, at meantime, complex analysis is very effective too.

7.1. Dislocations in Two-Dimensional Quasicrystals

The Burgers vector for dislocations in quasicrystals is, but for twodimensional quasicrystals which is due to.In the previous section, the plane elasticity and anti-plane

(6.6-8)

elasticity has been separated. If we consider only the plane elasticity, then the Burgers vector is .Since there are four components of the Burgers vector, the problem is quite complicated. By employing superposition principle, one can solve the single component problem separately, then obtain the total solution by superposing individual component solutions.

At first we solve the problem corresponding to component. Performing the Fourier transform

(7.1-1)

to Equation (6.3-11) yields

(7.1-2)

which is an ordinary differential Equation with the solution

(7.1-2)

in which there are four functions to be determined. By the boundary conditions (including dislocation condition and conditions at the infinity), we determine the unknown functions as below

(7.1-3)

where

(7.1-4)

(7.1-5)

(7.1-6)

In terms of the Fourier inversion calculation, the problem is solved and we have

(7.1-7a)

(7.1-7b)

(7.1-8a)

(7.1-8b)

(7.1-9a)

(7.1-9b)

(7.1-9c)

(7.1-10a)

(7.1-10b)

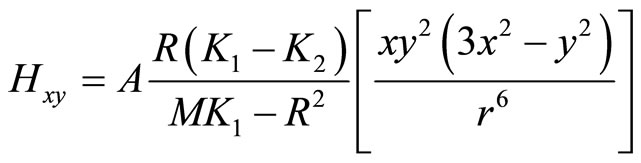(7.1-10c)

(7.1-10d)

where, a represents the size of dislocation core, and

(7.1-11).

These are the displacement field and stress field induced by the Burgers component. Similarly the solution induced by component corresponding to phason field can also be found and listed as follows

(7.1-12a)

(7.1-12b)

(7.1-12c)

(7.1-12d)

(7.1-13a)

(7.1-13b)

(7.1-13c)

(7.1-14a)

(7.1-14b)

(7.1-14c)

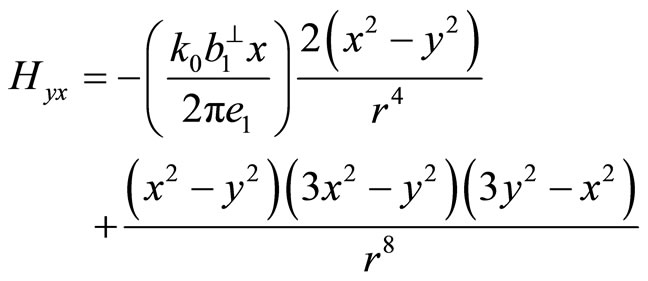(7.1-14d)

where

and c₀, c₁, c₂ and k₀ are

The above results show the phonon and phason are coupled each other, the solution is more complicated than that of crystals.

It is evident, the method developed here is systematiccal and direct, belong to a constructive approach, according to a straight forward step, the solution must be constructed. The correctness of the solutions can be examined by direct substituting. The method is effective not only for quasicrystals of fiveand ten-fold symmetries, but also for eightand twelve-fold symmetries. The detail can be found in [43,44].

7.2. Cracks in Two-Dimensional Quasicrystals

The above developed methods are successful not only for solving a series of dislocation problems, but also for crack problems. Due to the brittleness of the material under low and intermediate temperature, study on crack and fracture of quasicrystals is significant. Since cracks are a kind of twoor three-dimensional defects, which is more complex than dislocations which are one-dimensional defect. The complexity lies in the boundary conditions, the problem is concluded for solving some of dual integral Equations. This is a mathematiccally difficult problem. For example, for a Griffith crack in a decagonal (including pentagonal) quasicrystal, after the Fourier transform, the unknown functions do not reduced to algebraic Equations while the dual integral Equations, e.g.

(7.2-1)

It is fortune the integral Equations can be exactly solved, i.e.,

(7.2-2)

where is the first kind Bessel function of first order, the problem is solved. Through the Fourier inversion, we obtain the solution in physical space [51], the stresses and displacements induced by the crack are completely determined, the results are as follows

(7.2-3)

in which the meaning of the polar coordinates are shown in Figure 6.

The most important physical parameters in fracture theory are the stress intensity factor and energy release rate for the crack in decagonal and pentagonal quasicrystal are gained[51]:

(7.2-4)

(7.2-5)

The energy release rate indicates the all of phonon, phason and phonon-phason coupling make the contribution to the initiation of crack growth. Because this is an exact solution, provides useful information for brittle fracture quantitative study of brittle fracture of the novel material. The solutions for octagonal and dodecagonal quasicrystals have also been found following the similar procedure [43,44].

7.3. Dislocations in Three-Dimensional Quasicrystals

We pointed out again and again the importance of icosahedral quasicrystals in theory and practice, whose dislocation problem is also significant very much.

Yang et al [62] gave an approximate solution on dislocation in icosahedral quasicrystal under the condition,i.e., the phonon and phason do not couple.

We consider the assumption is incorrect, and must give the complete solution based on the strict Equation (6.6-9).

We study the problem caused by components and of the Burgers vector

.

Performing the Fourier transform (7.1-1) to Equation (6.6-9), then we obtain an ordinary differential Equation of six order, whose solution contain 6 unknown functions, which can be determined by boundary conditions, then takingthe Fourier inversion completes the solution. At last the displacement field is determined as follows

(7.3-1)

where, the radios of dislocation core, constants defined as below:

where

,

Though(7.3-1)is given the results induced by components, the other solutions can be similarly obtained. These results show the phonon-phason coupling is extremely important, this effect cannot be ignored. If phason and phonon-phason coupling are absence, the present solution reduced to the well-known dislocation solution of crystal:

Figures 7 and 8 draw the variations of displacements versus coordinates, and give a comparison with those of dislocation solution of crystals, in which the material constants are

,

and , in the computation, the case corresponding to the crystal. This work is given by work[63].

7.4. Cracks in Three-Dimensional Quasicrystals

The crack problem is more complicated than that of dislocation, the calculation is more complicated too. Paper [64] developed the Fourier transform and dual integral Equations method and gained the solution of a Griffith crack in icosahedral quasicrystal. Here only the displacement field is listed as below

(7.4-1)

where

(7.4-2)

the constants are as follows

(7.4-3)

, are composed from elastic constants and given as follows

(7.4-4)

and are defined as below

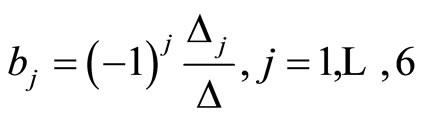(7.4-5)

(7.4-6)

in which the elements are

(7.4-7)

The crack energy release rate and crack opening displacement are depicted by Figures 9 and 10, respectively.

The above Fourier analysis extended the work of I N Sneddon [65] developed in the classical elasticity and fracture.

8. Analytic Solutions of Boundary Value Problems of Quasicrystals-Complex Analysis

The Fourier analysis developed above is fundamental and very important. However the calculation is often very complicated and lengthy. For the crack problems it is needed to solve some dual integral Equations, some among them will not be solved analytically and will not be in closed form always. For the notch problems, the Fourier analysis doesn’t work. So we must seek other analysis tools, among them the complex analysis is effective, powerful and beautiful method.

Since [43] the complex analysis on elasticity and fracture of quasicrystals has begun the probe. Succeeded work are papers [66-69], in which a systematical work have been carried out. We here discuss only the complex analysis on the boundary value problems of quadruple and sextuple harmonic Equations.

8.1. The Complex Analysis of Notch and Crack Problems in Two-Dimensional Quasicrystals-Solutions of Quadruple Harmonic Equation

The plane elasticity of quasicrystals of fiveand ten-fold symmetries can be concluded to solve the quadruple harmonic Equation:

(8.1-1)

The potential function, i.e., the solution of (8.1-1) has

the complex representation:

(8.1-2)

in which Re denotes the real part of a complex number, the complex variable, the conjugate, arbitrary analytic solution. Based on the relation between stress tensor and potential function, the stresses have the complex representation:

where

(8.1-4)

To determine the analytic solutions, it is needed to consider the boundary conditions.We study a notch problem shown in Figure 11, this problem cannot be solved by the Fourier transform method.

For simplicity, the tensile stress at infinity can be equivalent subjected onto surface of the notch, so we have the boundary conditions:

(8.1-5)

The boundary value problem (8.1-1), (8.1-4) and (8.1-5) cannot be solved directly at -plane, instead one can use the conformal mapping

(8.1-6)

(8.1-3)

to transform the problem for solving onto -plane. In this a way, the ellipse is mapped onto the unit circle (refer to Figure 12) at the mapping plane in which

.

The problem at last is reduced to solve the function Equation set, for the case the notch surface under the action of inner pressure, the function Equation set is where represents the value of at the unit circle, and

(8.1-8)

In addition

(8.1-9)

In terms of Cauchy integral and analytic extension principles, the solution of Equations set (8.1-7) as below:

In the above formulas if, the elliptic notch reduces to the Griffith crack, in the case the inversion of conformal mapping(8.1-6) is

(8.1-7)

(8.1-10)

(8.1-11)

Substituting the inversion into (8.1-10) one can obtain the solution at -plane such as

(8.1-12)

The solution in this version is quite simple and pretty, from which it is easy to determine the stress intensity factor and energy release rate:

The calculation is much simpler than that by using the Fourier transform.

8.2. The Complex Analysis of Notch and Crack Problems in Three-Dimensional Quasicrystals-Solutions of Sextuple Harmonic Equation

The power for solving notch/crack problems of icosahedral quasicrystals is more evident, the method is not only able solving the complicated defects problems those cannot be solved by other methods, but also quite simpler.

The plane elasticity of icosahedral quasicrystals is concluded to solve the sextuple harmonic Equation:

(8.2-1)

The complex representation of solution of the Equation is

(8.2-2)

where denotes any analytic functions (I = 1,2,···,6).

Taking similar manner to that in Subsection 8.1, the solution of an elliptic notch under tension or inner pressure at the mapping plane

(8.1-13)

(8.2-3)

As the notch reduces to a Griffith crack, by using the inversion (8.1-11) of conformal mapping (8.1-6), the solution at the physical plane is obtained, so the stress and displacement as follows, respectively

(8.2-5)

(8.2-6)

where

(8.2-7)

Furthermore we get the stress intensity factor and energy release rate of the crack:

(8.2-8)

We can do a comparison between the present results and those given in Subsection 7.4, and it is easy found that, the complex analysis is simpler very much than the Fourier analysis. Of course, this require us to learn and be familiar the complex function theory.

The above work is not only gained important information of elasticity and defects of quasicrystals, but also greatly extend and develop the complex analysis in the classical elasticity created by Muskhelishvili and his school [70].

9. Weak Solutions of Boundary Value Problems of Elasticity of Quasicrystal, Variational Principle and Finite Element

By using the analytic methods to treat elasticity and defects for various classes of quasicrystals mentioned above, we obtained a series of exact solutions, which satisfy all Equations and boundary conditions, and are called the classical solutions as well according to the terminology of mathematical physics. If people relax some requirements for determining solutions, one can obtain the so-called weak solutions, which are also named generalized solutions. The computer implementation of weak solutions needs some discretization. This is a modernized and systematical approach, which is important as the same as the analytic method. Due to the space limitation, we here give a discussion for the aspect in brief only.

9.1. The Uniqueness of Weak (Generalized) Solutions of Boundary Value Problems on Elasticity of Quasicrystals

Through some matrix representation [44,71], the Equation system of elasticity of quasicrystals can be written by an operator Equation

(9.1-1)

where is just the elastic matrix (4-12),

, is transpose of, represents the traction and generalized traction.

The boundary conditions are:

(9.1-2)

The uniqueness of the weak solutions can be proved, in the proof the Korn inequality will be used [44,71]. Because of the lengthy derivation, the detail is omitted here.

9.2. Variational Principle of Elasticity of Quasicrystals

Numerical methods, e.g. finite element method is one of methods to realizing weak solutions. The variational principle is a base of the finite element method. For the purpose, it is needed to introduce the variational principle of elasticity of quasicrystals.

9.2.1. Variational Principle of Elasticity of Quasicrystals

For a sufficient smooth boundary, if and satisfy the Equations of deformation geometry and displacement boundary conditions, the energy functional of quasicrystals

(9.2-1)

takes minimum, i.e.,

(9.2-2)

then they will be the solution satisfying the equilibrium Equations and the stress boundary conditions, in which is defined by

(9.2-2)

represents the region occupied by the quasicrystal, and the boundary of. The proof is omitted, the detail refer to [43,44].

9.3. Finite Element of Elasticity of Quasicystals and Numerical Example

A discretization of variational Equation (9.2-2) and region leads to the finite Element scheme of elasticity of quasicrystals, the detailed formulas can be found in [43,44].

Example Cylindrical tube of octagonal quasicrystal subjected to a inner pressure (Figure 13).

The boundary conditions are:

(9.3-1)

The Figure 14 illustrates the numerical solution of finite element computation.

10. Elasto-/Hydro-Dynamics and Defect Dynamics of Quasicrystals and Finite Difference Method and Solutions

10.1. Simple Elasto-/Hydro-Dynamics and Defect Dynamics of Quasicrystals

In the dynamic regime, the essential differences between phonons and phasons just can be profoundly revealed. Following argument given by [12,13], both phonons and phasons describe wave propagation in dynamic case. According to another argument suggested in [14-18], phonons describe wave propagation, while phasons describe diffusion. Corresponding to the first argument, the mathematical formulation is simpler. At the early time of quasicrystal study many researchers did dynamic analysis by taking this mode, e.g. [25,29,43,72-76]. Up to now there is no evident experimental results to verify wrongness of the argument. However much researchers turn to follow the argument of [14-18], e.g. work [77-81]. Considering the space limitation, we here discuss only for the study based on the mode proposed in [14-18].

In reference [78], the dynamic Equation set is

(10.1-1)

This is the simplest dynamic Equation set of quasicrystals, more complete one will be discussed in Section 14. In (10.1-1) denote the mass density, the diffusive coefficient, the kinetic coefficient of phason field, describing the relaxation of the motion, see [15]. The others are

(10.1-2)

and

(10.1-3)

This is a simplest Equation set of hydrodynamics of quasicrystals, which is simplified from the Equations of [14].

10.2. Application to the Elasticity and Fracture of Two-Dimensional Quasicrystals

Consider a quasicrystal of fiveor ten-fold symmetry, and direction is the direction of fiveor ten-fold axis. Under assumption(6.3-1), Equation set (10.1-1)-(10.1-3) are reduced to

(10.2-1)

where the second terms in left-hand side of the Equations are the manmade damping terms, pure numerical computational treatment, aimed to transfer to static case when the manmade damping constant to be taken a suitable value, so that the left-hand side tends to zero, and

(10.2-2)

Note that and behave the sense of the elastic waves, while  and  do not represent wave speeds, which are diffusive coefficients of phason field.

For the dynamic crack problem shown by Figure 15, we use finite difference method to solve crack of twodimensional quasicrystals In the case, when applied stress is varying with time, or the crack propagates with high speed, the problem must be doing a complete dynamic analysis. For the crack fast propagation, due to the moving of crack surface, this is a moving boundary problem, presents highly nonlinearity, which can be solved in approximate manner by numerical method only. Here we employ finite difference method for solving. Under corresponding boundary and initial conditions, Equation set (10.2-2) are solved by the finite difference approach, one finds the dynamic stress intensity factor given by Figure 16 (see e.g. [78], or [44] for the detail)

The figure shows that the difference between results of quasicrystal and crystal is quite evident. The computation is carried out for decagonal Al-Ni-Co quasicrystal with material constant

for quasicrystal, for crystal.

10.3. Application to Elastodynamics and Fracture Dynamics of Three-Dimensional Quasicrystals

Of course the dynamic study for three-dimensional quasicrystals is more important. Here consider icosahedral quasicrystals. Assume the axis to be the direction of Five-fold axis. Under assumption (6.5-6), the dynamic Equations (10.1-1)-(10.1-3) are reduced to

(10.3-1)

where

(10.3-2)

Note that and represent speeds of elastic waves, while and are not wave speeds, which are diffusive coefficients of phasons. The numerical analysis is given for the specimen shown in Figure 17 made of icosahedral quasicrystal. After finite difference treatment on Equation set (10.3-1) and corresponding boundary and initial conditions, the dynamic stress intensity factor for initiation of crack growth is obtained and shown in Figure 18. In the computation the material is icosahedral Al-Pd-Mn quasicrystal with material constants:,

,

for quasicrystal, and for crystal. It is evident that the results between quasicrystal and crystal are quite large.

The dynamic stress intensity factor for fast crack propagation of the central specimen is illustrated in Figure 17, which comes from monograph [44].

The oscillation of the curve comes from the interfereence and reflection of waves, in which there are reasons come from numerical computation, it is needed doing further study.

10.4. Finite Difference Scheme

The detail on the difference scheme employed in the above is described as Figure 19 (in the case we take for simplicity).

Taking time step and the central difference, then dynamic Equation set (10.2-2) has the difference scheme within network

(10.4-1)

at boundary and.

(10.8-2a)

(10.4-2)

(10.4-3)

(10.4-4)

and

(10.4-4)

At and, there are

(10.4-5)

(10.4-6)

(10.4-7)

In addition, approximately

(10.4-8)

At corner points

(10.4-9)

Similarly, the differences of displacements at and refer to Fan [44].

11. Plasticity and Nonlinear Fracture of Quasicrystals

Quasicrystals present brittle at conventional and low temperature, but dramatically present plasticity at high temperature. This aroused the interest of researchers.

11.1. Measurement of Plastic Deformation of Quasicrystals

Through experiments, researchers measured the plastic deformation process of some quasicrystals. Figure 20 is the stress-strain curve of icosahedral Al-Pd-Mn quasicrystals, which gives a good description on plastic deformation. Among the influence factors to the plastic

deformation, temperature is important, the strain rate is also significant. Here the measurement is carried out under rate . The ductile-brittle transition temperature is very high, 690˚C, and 730˚C - 800˚C is the high temperature scale.

Different from icosahedral quasicrystals, the two-dimensional quasicrystals have a direction of periodic symmetry, so that the plastic deformation of which is different from that of the former. Figure 21(a) gives the diagram of the plastic deformation of decagonal Al-Ni-Co quasicrystal [82]. Due to the coexistence of periodic and quasiperiodic symmetries, the plastic deformation presents anisotropic Figure 21 (b) depicted the orientation of the specimens: vertical, parallel and to the periodic symmetry direction.

The Germany scientists carried out a series of experimental studies on plasticity of quasicrystals[82-91]. The results show that, the mechanism of plastic deformation of quasicrystals is movement of dislocations. The mechanism is the same as in crystals. But there are quite different points to that in crystals at meantime. One of the most different points is the existence of phason variables. What is the effect of phason field to the plastic deformation of the new phase? However the mechanism about this is not clear. Though there are people try to give some explanations on plastic deformation by using dislocation model and so on, the problem is substantively unsolved so far. Due to lack of enough experimental data in macroscopy, the constitutive Equation of plasticity of quasicrystals has not been set up.

This leads to difficulty doing stress analysis of the material. One can say that the study is in an infant stage.

In spite of these difficulties, people pay effort to do some work as pointed out above, the experiments reported in Refs [82-91] provide some hints, which are beneficial for the stress analysis for plasticity and defects

of the material. In the following some semi-phenomenological and semi-theoretical results are listed, they may provide a reference for the researchers in the communicate.

11.2. Generalized Cohesive Force Model [92-95]

Due to lack of constitutive Equation of plasticity of quasicrystals up to now, it may be a possible way that we draw the results of classical plasticity, classical dislocation theory and classical nonlinear fracture theory to study some relevant problems in quasicrystals. A useful model in classical elasto-plastic fracture theory is socalled Dugdale-Barenblatt model, the paper [92] extended it to plastic analysis of quasicrystals, and named it be generalized Dugdale-Barenblatt model, the classical work has been done by [93] and [94]. In terms of the model, we determined the size of plastic zone around the crack tip of anti-plane problem of one-dimensional hexagonal quasicrystals

(11.2-1)

and the crack tip opening displacement

(11.2-2)

and the plastic solution of plane problem of two-dimensional quasicrystals by [92]

(11.2-3)

(11.2-4)

and solution of three-dimensional icosahedral quasicrystals by

(11.2-5)

where

(11.2-6)

and

.

The curve drawn from (11.2-5) refer to Figure 22, which shows the effect of phason and phonon-phason coupling is significant.

11.3. Generalized Continuum Dislocations Model [96]

We developed the continuous dislocation model, Fan et al. [96] which is originated from the classical BCS model [97,98] for crystals. For the instance, the boundary value problem of partial differential Equations is reduced into for solving the following equivalent singular integral Equation of Cauchy kernel

(11.3-1)

in which represents dislocation density. The singular integral Equation of Cauchy kernel (11.3-1) has been systematically studied by monograph [99]. At present case the Equation can be solved exactly, it follows the size of plastic zone at the crack tip and the crack tip opening displacement, etc. The results are exactly identical to those given in Subsection 11.2. The correctness of the solutions are examined each other by different physical models and different mathematical tolls.

11.4. Model Based on Generalized Eshelby Energy-Momentum Tensor [100]

The generalized Dugdale-Barenblatt model and generalized continuum dislocation model, are quite different physically and mathematically, yield amazingly the complete identical solutions, we realized that there exist some inherent connection between the two models. Paper [100] gave a probe for the question. They proposed the generalized energy-momentum tensor of quasicrystals (for crystal the tensor was given by [101])

(11.4-1)

and generalized integral of path independency

(11.4-2)

and found that they are the uniformly theoretical base of generalized Dugdale-Barenblatt model and generalized continuum dislocations model.

12. Phenomenological Theory of Lattice Dynamics of Quasicrystals

Due to existence of quasiperiodic translational symmetry,

the quasicrystals behave lattice, even if which is not periodic lattice. The lattice dynamics is very complicated, which is related not only to phonons, but also phasons and phonon-phason coupling. A simple treatment is based on the dynamic model of [12,13]. Starting from the point of view, the author [73] discussed lattice dynamics of one-dimensional hexagonal quasicrystals. Then [102] studied the problem for dodecagonal quasicrystals. Recently [103] gave a simple treatment for the problem for icosahedral quasicrystals. They found the lattice specific heat and thermodynamic functions. The work [74,75] made a more comprehensive study decagonal and icosahedral Al-Pd-Mn quasicrystals. But the study in this respect there are much difficulties.

13. Mathematical Theory of Energy Spectrum of Electronic Structure of Quasicrystals

After the discovery of quasicrystals, scholars use the Schroedinger Equation

(13-1)

to study the energy spectrum of electronic structure of quasicrystals, where

(13-2)

denotes the Schroedinger operator, h the Planck constant, V(r) the potential energy, E the energy eigenvalue, the wave function. For crystals, there is periodicity

(13-3)

Bloch assume that

(13-4)

where represents the period of lattice. The wave function can be expressed by

(13-5)

Expression (13-5) is named Bloch theorem which leads to the great progress of energy spectrum analysis of crystals, forms the energy band theory etc, constitutes one of basis of solid physics. The quasicrystals do not satisfy the periodic translational symmetry (13-3), they have no the Bloch theory, the solving Schroedinger Equation faces a great difficulty.

In terms of Fibonacci model, solving discrete Schroedinger Equation, one found many meaningful results [104-118]. The detail can be found the references.

14. Elasto-/Hydro-Dynamics of Quasicrystals in Soft Matter

The above description told that the quasicrystals were observed in binary and ternary metallic alloys first for three-dimensional icosahedral quasicrystals and twodimensional 5-, 10-, 8- and 12-fold symmetry quasicrystals then. Recently the structure was discovered in colloidal solutions [119,120], polymers [121-123] and nanoparticle mixture [124]. Especially the work reported by Ref [119] has aroused the great interest of researchers, because the 18-fold quasicrystal was the first observed. From the view point of symmetry, the possible 7-, 14-, 9- and 18-fold quasicrystals in solid phase have been predicated by reference [125] at an earlier time. For 7-, 14-, 9- and 18-fold quasicrystals, by using group representation theory, a “six-dimensional embedding space” concept was proposed in Ref [125]. According to the concept, there are two phason fields apart from phonon field, i.e., the phase angle of order parameter of the density of quasicrystals

(14-1)

in which represents phonon field which is the same as previous and the first phason field, the second phason field which was discussed in the previous sections. So that

(14-2)

denotes the strain tensor associated with the first phason field. If we define the relevant stress tensor and elastic constant tensors then the generalized Hooke’s law is

(14-3)

in which have the same meaning to those defined previously, while is the stress tensor associated with strain tensor, the coupling elastic constant tensor between phonon-first phason fields (the coupling field), coupling elastic constant tensor between first and second phason fields (the coupling field). This means there are pnonon-phason coupling and phason-phason coupling. In addition the effects due to fluid must be considered, i.e., we must study the hydrodynamics of quasicrystals in soft matter. This theory has not been existed beforehand yet. The references [126-129] report a preliminary probe in this respect.

The work reported in Refs [119-124] opens a fascinating area, concerning quasicrystals in soft matter. To develop the theory, we suggest a novel intermediate solidliquid phase quasicrystals. This new structure may be a description of quasicrystals observed in soft matter to date, advances widely the theoretical understanding of quasicrystals, and presents importance to engineering application of quasicrystals as a novel functional and structural material.

From the application angle, the mechanical behaviour of the possible solid-liquid phase quasicrystals is one of basic problems. It is fortunate the theoretical framework on the new quasicrystalline phase can be drawn from the elasto-/hydro-dynamics of Lubensky et al. [14-18] though the theory of Lubensky et al. is not directed to the soft matter in that time. However for 18-fold symmetry we must combine the theory of Lubensky et al with the use of the so-called “six-dimensional embedded space” concept proposed in [125].This combination may allow us to set up a new theory in studying the novel quasicrystalline phase, at least for its continuum mechanics. But the problem is tremendous complex. To overcome the difficulty, we develop a theory in [126-129], and some solutions may be found.

Considering the fact that the 12-fold quasicrystals in different soft matters were discovered frequently and the 18-fold quasicrystal in colloids first observed, one can focus on the discussion on these two kinds of quasicrystals and their mechanical behaviour. The hint of mechanics of liquid crystals, the combination between hydrodynamics suggested by Lubensky et al. and six-dimensional embedding space help us to make some achievements [126-129].

15. Conclusions and Discussion

The review is mainly on the mechanics of solid quasicrystals, and the soft matter quasicrystals are just touched preliminarily. The areas belong to the well studied branches in quasicrystals science. In due of the progress of experimental study and observation technique, there may be more kinds of quasicrystals discovered, and more material constants measured. The current and potential applications exhibit the importance of the materials.

To explore some essentials and to serve the applications, the mathematical theory of elasticity and defects of solid quasicrystals present significance, which has been well developed. However the research of much of important subjects, e.g. the plasticity, dynamics etc is still in infant situation.

The mathematical theory of elasticity of solid quasicrystals presents fundamental importance, not only in theoretical sense but also in practice. The theory has given many applications, for example, in dislocation stress analysis, fracture mechanics, etc, these are meaningful to materials science and technology as well as in mechanical engineering. The theory and results in the respects moreover help the plastic analysis due to the lack of plastic constitutive Equations of the novel material.

The study of the mathematical theory of elasticity of solid quasicrystals promotes the development of some branches of applied mathematics, e.g. applied complex, variational principle, numerical analysis, etc.

The study on elasticity, viscosity, hydrodynamics etc of soft matter quasicrystals begins just, but opens a broad area and will promote a further development of the quasicrystal science, in which some mathematical aspects, e.g. the Poisson’s brackets in condensed matter physics, Lie groups and Lie algebra etc play important role, but we here cannot discussed due to space limitation. In the research work of soft matter quasicrystals, the methodology and results of solid quasicrystals been achieved are useful.

Apart from the above reviewed works, there are many publications in the field, e.g. [130-134] etc., which are very significant, though have not been reviewed here due to the limitation of the space.

16. Acknowledgements

The author thanks the support of the National Natural Science Foundation of China (through grants11272053, 10672022, 10372016 and K19972011) and the Alexander von Humboldt Foundation of Germany over the years. The thanks are also to Professor U. Messerschmidt in the Max Planck Institut fuerMikrostrukturPhysik in Halle in Germany for helpful discussions.

REFERENCES