Applied Mathematics
Vol.5 No.4(2014), Article ID:43573,5 pages DOI:10.4236/am.2014.54064
Lattices Associated with a Finite Vector Space
Mengtian Yue
Office of Scientific Research, Langfang Teachers’ College, Langfang, China
Email: ymtxyz@126.com
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 23 December 2013; revised 23 January 2014; accepted 30 January 2014
ABSTRACT
Let  be a n-dimensional row vector space over a finite field
be a n-dimensional row vector space over a finite field . For
. For , let
, let  be a ddimensional subspace of
be a ddimensional subspace of .
.  denotes the set of all the spaces which are the subspaces of
denotes the set of all the spaces which are the subspaces of  and not the subspaces of
and not the subspaces of 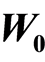 except
except . We define the partial order on
. We define the partial order on  by ordinary inclusion (resp. reverse inclusion), and then
by ordinary inclusion (resp. reverse inclusion), and then  is a poset, denoted by
is a poset, denoted by 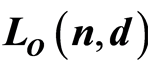 (resp.
(resp. ). In this paper we show that both
). In this paper we show that both  and
and  are finite atomic lattices. Further, we discuss the geometricity of
are finite atomic lattices. Further, we discuss the geometricity of  and
and , and obtain their characteristic polynomials.
, and obtain their characteristic polynomials.
Keywords:Vector Space; Geometric Lattice; Characteristic Polynomial

1. Introduction
Let P be a poset. For , we say a covers b, denoted by
, we say a covers b, denoted by ; if
; if  and there doesn’t exist
and there doesn’t exist  such that
such that . If P has the minimum (resp. maximum) element, then we denote it by 0 (resp. 1) and say that P is a poset with 0 (resp. 1). Let P be a finite poset with 0. By a rank function on P, we mean a function r from P to the set of all the integers such that
. If P has the minimum (resp. maximum) element, then we denote it by 0 (resp. 1) and say that P is a poset with 0 (resp. 1). Let P be a finite poset with 0. By a rank function on P, we mean a function r from P to the set of all the integers such that  and
and  whenever
whenever . Observe the rank function is unique if it exists. P is said to be ranked whenever P has a rank function.
. Observe the rank function is unique if it exists. P is said to be ranked whenever P has a rank function.
Let P be a finite ranked poset with 0 and 1. The polynomial  is called the characteristic polynomial of P, where
is called the characteristic polynomial of P, where  is the
is the  function on P and r is the rank function of P. A poset P is said to be a lattice if both
function on P and r is the rank function of P. A poset P is said to be a lattice if both  and
and  exist for any two elements
exist for any two elements .
.  and
and  are called the join and meet of a and b, respectively. Let P be a finite lattice with 0. By an atom in P, we mean an element in P covering 0. We say P is atomic if any element in
are called the join and meet of a and b, respectively. Let P be a finite lattice with 0. By an atom in P, we mean an element in P covering 0. We say P is atomic if any element in  is the join of atoms. A finite atomic lattice P is said to be a geometric lattice if P admits a rank function
is the join of atoms. A finite atomic lattice P is said to be a geometric lattice if P admits a rank function  satisfying
satisfying ,
, . Notations and terminologies about posets and lattices will be adopted from books [1] [2] .
. Notations and terminologies about posets and lattices will be adopted from books [1] [2] .
The special lattices of rough algebras were discussed in [3] . The lattices generated by orbits of subspaces under finite (singular) classical groups were discussed in [4] [5] . Wang et al. [6] -[8] constructed some sublattices of the lattices in [4] . The subspaces of a d-bounded distance-regular have similar properties to those of a vector space. Gao et al. [9] -[11] constructed some lattices and posets by subspaces in a d-bounded distance-regular graph. In this paper, we continue this research, and construct some new sublattices of the lattices in [4] , discussing their geometricity and computing their characteristic polynomials.
Let  be a finite field with q elements, where q is a prime power. For a positive integer
be a finite field with q elements, where q is a prime power. For a positive integer , let
, let  be the n-dimensional row vector space over
be the n-dimensional row vector space over . Let
. Let . For a fixed
. For a fixed -dimensional subspace
-dimensional subspace  of
of , let
, let .
.
If we define the partial order on  by ordinary inclusion (resp. reverse inclusion), then
by ordinary inclusion (resp. reverse inclusion), then  is a poset, denoted by
is a poset, denoted by  (resp.
(resp. ). In the present paper we show that both
). In the present paper we show that both 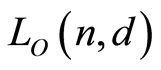 and
and  are finite atomic lattices, discuss their geometricity and compute their characteristic polynomials.
are finite atomic lattices, discuss their geometricity and compute their characteristic polynomials.
2. The Lattice 
In this section we prove that the lattice  is a finite geometric lattice, and compute its characteristic polynomial. We begin with a useful proposition.
is a finite geometric lattice, and compute its characteristic polynomial. We begin with a useful proposition.
Proposition 2.1. ([12] , Lemma 9.3.2 and [13] , Corollaries 1.8 and 1.9). For , the following hold:
, the following hold:
1) The number of k-dimensional subspaces contained in a given m-dimensional subspace of  is
is
 .
.
2) The number of m-dimensional subspaces containing a given k-dimensional subspace of  is
is
 .
.
3) Let P be a fixed m-dimensional subspaces of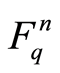 . Then the number of k-dimensional subspaces Q of
. Then the number of k-dimensional subspaces Q of  satisfying
satisfying  is
is
 .
.
Theorem 2.2.  is a geometric lattice.
is a geometric lattice.
Proof. For any two elements ,
,

Therefore  is a finite lattice. Note that
is a finite lattice. Note that  is the unique minimum element. Let
is the unique minimum element. Let  be the set of all the
be the set of all the  -dimensional subspaces of
-dimensional subspaces of , where
, where . Then
. Then  is the set of all the atoms in
is the set of all the atoms in . In order to prove
. In order to prove  is atomic, it suffices to show that every element of
is atomic, it suffices to show that every element of  is a join of some atoms. The result is trivial for
is a join of some atoms. The result is trivial for . Suppose that the result is true for
. Suppose that the result is true for . Let
. Let . By Proposition 2.1 and
. By Proposition 2.1 and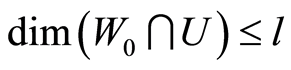 , the number of
, the number of  -dimensional subspaces of
-dimensional subspaces of  contained in
contained in  at least is
at least is
 .
.
Therefore there exist two different l-dimensional subspaces  of
of  such that
such that . By induction
. By induction is a join of some atoms. Hence
is a join of some atoms. Hence  is a finite atomic lattice. For any
is a finite atomic lattice. For any  , define
, define . It is routine to check that
. It is routine to check that  is the rank function on
is the rank function on . For any
. For any , we have
, we have

Hence  is a geometric lattice.
is a geometric lattice. 
Lemma 2.3. For any , suppose that
, suppose that ,
,  and
and . Then the
. Then the  function of
function of  is
is

Proof. The  function of
function of  is
is

By Proposition 2.1, we have
 .
.
Thus, the assertion follows. 
Theorem 2.4. The characteristic polynomial of  is
is

Proof. By Proposition 2.1 and Lemma 2.3, we have

3. The Lattice 
In this section we prove that the lattice  is a finite atomic lattice, classify its geometricity and compute its characteristic polynomial.
is a finite atomic lattice, classify its geometricity and compute its characteristic polynomial.
Theorem 3.1. The following hold:
1) 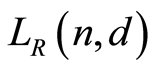 is a finite atomic lattice.
is a finite atomic lattice.
2)  is geometric if and only if
is geometric if and only if .
.
Proof. 1) For any two elements ,
,  and
and

Therefore  is a finite lattice. Note that
is a finite lattice. Note that 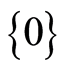 is the unique minimum element. Let
is the unique minimum element. Let  be the set of all the j-dimensional subspaces of
be the set of all the j-dimensional subspaces of , where
, where . Then
. Then  is the set of all the atoms in
is the set of all the atoms in . In order to prove
. In order to prove  is atomic, it suffices to show that every element of
is atomic, it suffices to show that every element of  is a join of some atoms. The result is trivial for
is a join of some atoms. The result is trivial for . Suppose that the result is true for
. Suppose that the result is true for . Let
. Let . By Proposition 2.1, the number of
. By Proposition 2.1, the number of  subspaces of
subspaces of  containing
containing  is equal to
is equal to
 .
.
Then there exist two different  subspaces
subspaces  such that
such that . By induction
. By induction  is a join of some atoms. Therefore
is a join of some atoms. Therefore  is a finite atomic lattice.
is a finite atomic lattice.
2) For any , we define
, we define . It is routine to check that
. It is routine to check that  is the rank function on
is the rank function on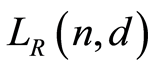 . It is obvious that
. It is obvious that  is a geometric lattice. Now assume that
is a geometric lattice. Now assume that . Let P be a
. Let P be a  -dimensional subspace of
-dimensional subspace of  and
and . By Proposition 2.1, the number of 2-dimensional subspaces of
. By Proposition 2.1, the number of 2-dimensional subspaces of  containing P is equal to
containing P is equal to

Therefore, there exist two different 2-dimensional subspaces  such that
such that . So
. So ,
, . Hence
. Hence , which implies that
, which implies that  is not a geometric lattice when
is not a geometric lattice when .
. 
Lemma 3.2. For any , suppose that
, suppose that ,
,  and
and . Then the
. Then the  function of
function of  is
is

Proof. The  function of
function of  is
is

Proposition 2.1 implies that
 .
.
Theorem 3.3. The characteristic polynomial of  is
is
 .
.
Proof. By Proposition 2.1, we have

References
- Aigner, M. (1979) Combinatorial Theory. Springer-Verlag, Berlin. http://dx.doi.org/10.1007/978-1-4615-6666-3
- Wan, Z. and Huo, Y. (2004) Lattices Generated by Transitive Sets of Subspaces Under Finite Classical Groups. 2nd Edition, Science Press, Beijing.
- Liu, Y.H. (2011) Special Lattice of Rough Algebras. Applied Mathematics, 2, 1522-1524. http://dx.doi.org/10.4236/am.2011.212215
- Huo, Y.J. and Wan, Z.-X. (2001) On the Geomericity of Lattices Generated by Orbits of Subspaces under Finite Classical Groups. Journal of Algebra, 243, 339-359. http://dx.doi.org/10.1006/jabr.2001.8819
- Gao, Y. and You, H. (2003) Lattices Generated by Orbits of Subspaces under Finite Singular Classical Groups and Its Characteristic Polynomials. Communications in Algebra, 31, 2927-2950. http://dx.doi.org/10.1081/AGB-120021900
- Wang, K.S. and Guo, J. (2009) Lattices Generated by Two Orbits of Subspaces Under Finite Classical Groups. Finite Fields and Their Applications, 15, 236-245. http://dx.doi.org/10.1016/j.ffa.2008.12.008
- Wang, K.S. and Li, Z.T. (2008) Lattices Associated with Vector Spaces Over a Finite Field. Linear Algebra and Its Applications, 429, 439-446. http://dx.doi.org/10.1016/j.laa.2008.02.035
- Guo, J., Li, Z.T. and Wang, K.S. (2009) Lattices Associated with Totally Isotropic Subspaces in Classical Spaces. Linear Algebra and Its Applications, 431, 1088-1095. http://dx.doi.org/10.1016/j.laa.2009.04.009
- Gao, S.G., Guo, J. and Liu, W. (2007) Lattices Generated by Strongly Closed Subgraphs in d-Bounded Distance-Regular Graphs. European Journal of Combinatorics, 28, 1800-1813. http://dx.doi.org/10.1016/j.ejc.2006.05.011
- Guo, J. and Gao, S.G. (2008) Lattices Generated by Join of Strongly Closed Subgraphs in d-Bounded Distance-Regular Graphs. Discrete Mathematics, 308, 1921-1929. http://dx.doi.org/10.1016/j.disc.2007.04.043
- Guo, J. and Wang, K.S. (2010) Posets Associated with Subspaces in a d-Bounded Distance-Regular Graph. Discrete Mathematics, 310, 714-719. http://dx.doi.org/10.1016/j.disc.2009.08.014
- Brouwer, A.E., Cohen, A.M. and Neumaier, A. (1989) Distance-Regular Graphs. Springer-Verlag, New York. http://dx.doi.org/10.1007/978-3-642-74341-2
- Wan, Z. (2002) Geometry of Classical Groups over Finite Fields. 2nd Edition, Science Press, Beijing/New York.

