ABSTRACT

A class of martingale estimating functions based on the first two moments of the observed process provides a convenient framework for estimating the parameters of diffusion processes [1]. In the Bayesian set up, combined estimating functions had been studied for diffusion processes in [2] with filtering applications. However, when the conditional mean and the conditional variance are functions of parameters of interest in a diffusion process model, the basic martingales generating components of quadratic estimating functions are such that one is an absolute continuous function with respect to the other [3, p. 94]. Hence, the combined martingale estimating functions cannot be constructed for continuous-time diffusion processes. In this paper, a general framework for parameter estimation of discretely observed interest rate models is developed by using the Milstein approximation and closed form expressions for the information gain are also obtained. The method is used to study the estimates of the parameters for an extended version of the CoxIngersoll-Ross interest rate model.

1. Introduction

Inference for discrete-time stochastic processes using estimating functions was discussed in [4]. In [1] and [5], estimation for semimartingales was studied using estimating functions. In addition, filtering and prediction problems were studied in [6] and [2] using estimating functions in the Bayesian context.

The standard method of estimation for parameters in the drift coefficient of interest rate models [7] involves the calculation of a likelihood ratio (Radon-Nikodym derivative) and hence the maximum likelihood estimator(s). This is less than straightforward for complicated models, and indeed it is not available at all because of the non-existence of the Radon-Nikodym derivative. The estimating function method, however, allows estimators to be obtained straightforwardly under very general conditions on the first two conditional moments [3, p. 131]. They can deal, in particular, with the situation in which the Brownian motion in a diffusion is replaced by a general square-integrable martingale as in [1]. The combined estimating function approach used in this paper, based on selection of an optimal estimating function from within a specified class of martingale estimating functions, involves assumptions on the first four conditional moments of the underlying process. In most realistic situations the diffusions cannot be observed continuously, so discrete time approximation to stochastic integrals or a direct approach using the discrete time observations is required.

Recently in [8], among others, the estimating functions approach was used to study the estimation problems for some discretely observed interest rate models. However, these methods involve the closed form expressions for the first four conditional moments, obtained by Ito’s approximations, and these are not available for general time-homogeneous diffusion process models and in particular for an extended CIR interest rate model.

In [9], the asymptotic theory of the maximum likelihood estimator for diffusion models was studied, first by using Milstein’s approximation of diffusion processes [10], and further by approximating the conditional transition density by a normal density by ignoring the skewness and kurtosis.

In this paper, we study combined martingale estimating functions for interest rate models and show that the combined estimating functions are more informative when the conditional mean and variance of the observed process depend on the parameter of interest. This paper is organized as follows. The rest of Section 1 presents the basics of estimating functions and information associated with estimating functions for discrete-time stochastic processes. Section 2 presents combined estimating functions for discretely observed continuous-time diffusion processes based on closed form expressions for the first four conditional moments via Itô’s formula. In Section 3, the theory of combined estimating functions is applied to general diffusion processes.

Suppose that is a realization of a discrete-time stochastic process and its distribution depends on a vector parameter belonging to an open subset of the p-dimensional Euclidean space. Let denote the underlying probability space, and let be the σ-field generated by. Let , be specified q-dimensional vectors that are martingales. We consider the class of zero mean and square integrable p-dimensional martingale estimating functions of the form

where are matrices depending on ,. The estimating functions are further assumed to be almost surely differentiable with respect to the components of θ and such that

and are nonsingular for all and for each. The expectations are always taken with respect to. Estimators of θ can be obtained by solving the estimating equation. Furthermore, the matrix

is assumed to be positive definite for all. Then in the class of all zero mean and square integrable martingale estimating functions, the optimal estimating function which maximizes, in the partial order of nonnegative definite matrices, the information matrix

is given by

and the corresponding optimal information reduces to

.

The function is also called the optimal estimating function and has properties similar to those of a score function in the sense that and

.This is a more general result in the sense that for its validity we do not need to assume that the true underlying distribution belongs to the exponential family of distributions. Moreover, it follows from [11, p. 916] that if we solve an unbiased estimating equation to get an estimator, then the asymptotic variance of theresulting estimator is the inverse of the information. Hence the estimator obtained from a more informative estimating equation is asymptotically more efficient.

2. Combined Estimating Functions for Discretely Observed Diffusions

In this section, we discuss the discrete time results on combining estimating functions and obtain the closed form expression for the gain in information. Assume the real-valued continuous time process is recorded discretely at the time points where h is the discrete interval of observations of. Now we consider the observable discrete-time process with conditional moments

(2.1)

(2.2)

(2.3)

(2.4)

where is the σ-field generated by

. That is, we assume that the third and the forth moments of do not contain any additional parameters. In order to estimate the parameter θ based on the observations, we consider two classes of martingale differences

and

, where the quadratic variation and covariation of and are

and

respectively. The optimal estimating functions based on the martingale differences and, and the corresponding information are given by

(2.5)

(2.6)

The following theorem provides optimality of the combined estimating function based on martingales and for the multi-parameter case.

Theorem 1. For a discretely observed process, in the class of all combined estimating functions of the form

(a) The optimal estimating function is given by

, where

and

(b) the information is given by

(c) the gain in information is given by

Example 1 (Combined Estimating Functions for CoxIngersoll-Ross Model). Recently there has been a growing interest in studying inference for interest rate models. In most realistic situations, the diffusion cannot be observed continuously, so discrete time approximations to stochastic integrals or a direct approach using discrete time observations is required. As a concrete illustration of the methodology, we shall discuss the estimation for the Cox, Ingersoll and Ross [12] short-term interest rate model of the form

(2.7)

with, , , and is the standard Brownian motion. The unknown parameters of interest are. Let

. It is of interest to note that in this example we can obtain the closed form expressions for the first four conditional moments by using Itô’s formula for,.The first four conditional moments of yth are calculated as (see Appendix A for the details):

(2.8)

(2.9)

(2.10)

and

(2.11)

Then based on the discretely observed observations the martingale differences are

, and Also,

and

The derivatives are given by

(2.12)

(2.13)

Hence, the optimal estimating functions based on the martingale differences and the corresponding information matrix are given by

(2.14)

where

Similarly, the optimal estimating functions based on the martingale differences and the corresponding information matrix are given by

(2.15)

where

The optimal combined estimating function using and is given by

(2.16)

where

and

Further, let be the matrix

(2.17)

where

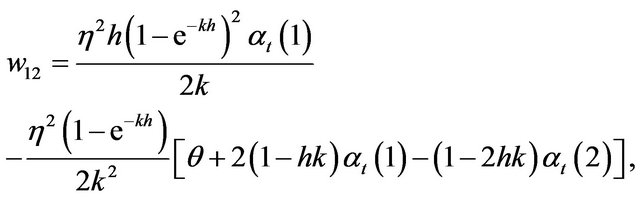
The information associated with the optimal combined estimating function is

Note: If we allow η in (2.7) to be a function of k, then the estimating function and the combined estimating function become intractable.

3. Combined Estimating Functions for General Models

For extended versions of the CIR model, closed form expressions for the first four conditional moments cannot be obtained easily by using Itô’s formula, as was done for the CIR model. Recently, the Milstein’s approximation was used in [9] to obtain the first two conditional moments of the diffusion. In this section, we use Milstein’s approximation to obtain the first four conditional moments and construct the optimal estimating functions.

Consider the diffusion process given by the time-homogeneous stochastic differential equation of the form

(3.1)

Where a and b are the drift and diffusion functions, respectively, and is the standard Brownian motion.

A special case of (3.1) is the Brownian motion with constant drift and diffusion:

where. In this case, the conditional distribution of given is a normal with mean and variance. If we consider the geometric Brownian motion given by

with, then becomes a Brownian motion with drift with and. In this case, the conditional distribution of given is also normal. The CIR process can be re-parameterized to the following form:

In this case, we have computed the first four conditional moments of the process to use in an estimating function framework. Extended versions of the CIR process model have been proposed for modeling interest rate processes. For example, some consider the constant elasticity of variance process of the form

or the nonlinear drift diffusion process [13] given by

For more general extended models, the diffusion is a function of the observation y_t and hence, closed form expressions of the conditional distributions, as well as closed form expressions for the conditional moments cannot be easily obtained by solving differential equations obtained by repeated application Itô’s formula. However, Milstein’s approximation can be used to obtain the first four conditional moments.

Milstein’s approximation applied to (3.1) produces

(3.2)

where and, i.i.d. Unlike the Euler approximation for diffusion processes, the Milstein approximation does not yield a conditional normal distribution for The distribution implied by the Milstein approximation is a mixture of a normal and chisquare distributions. By using (3.2), the first four conditional moments of given are approximated by

(3.3)

(3.4)

(3.5)

(3.6)

Then based on the discretely observed observations the martingale differences are , and. In this case, we have

(3.8)

(3.9)

(3.10)

In addition, if we let, then

(3.11)

The optimal estimating functions based on the martingale differences and, and the corresponding information are given by

(3.12)

(3.13)

The combined estimating function and the corresponding information follow from Theorem 1 by taking.

Example 2 (NLD Process).The nonlinear drift (NLD) diffusion process for modeling interest rates was introduced in [13]. Here we consider the following NLD

(3.14)

where, , , and. These parameter ranges are chosen to guarantee a positive recurrent solution to the SDE. For this process,

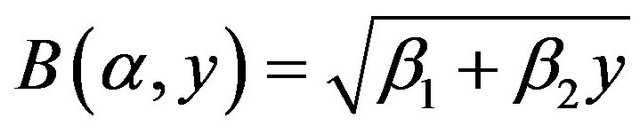, , and

. The Milstein approximation gives the following discretized version of the process:

(3.15)

In this case, we have the following for the first four conditional moments of the discretized process:

(3.16)

(3.17)

(3.18)

(3.19)

The estimating function and corresponding information based on are given by

(3.20)

where

Moreover, the estimating function and corresponding information based on M_t are given by

(3.21)

where

In this case, and the optimal combined estimating function using and is given by, where

with

and

The information for the combined estimating function

is given by

4. Conclusion

For discretely observed general interest rate models, the combined estimating function method allows estimators to be obtained straightforwardly under very general conditions on the first four conditional moments. In this paper, we have studied inference for interest rate models, first by using the Milstein approximation, and then combining estimating functions using martingale differences and have obtained the closed form expression for the information gain.

REFERENCES

Moments of the CIR Process

The first four conditional moments of the CIR process

may be obtained by using Itô’s formula on successive powers of the process. This gives

with as an initial condition. We let

, so that the first four conditional moments of satisfy the following differential equations:

with initial conditions, , , and. Solving the differential equations in turn yields:

Hence, the first four conditional centered moments are given as