ABSTRACT

The solutions of the Alhaidari formalism of the Dirac equation for the gravitational plus exponential potential have been presented using the parametric Nikiforov-Uvarov method. The energy eigenvalues and the corresponding un-normalized eigenfunctions are obtained in terms of Laguerre polynomials.

1. Introduction

The bound state solutions of the Dirac equation are only possible for some potentials of physical interest [1-5]. These solutions could be exact or approximate and they nornally contain all the necessary information for the quantum system. Quite recently, several authors have tried to solve the problem of obtaining exact or approximate solutions of the Dirac equation for a number of special potentials using different methods [6-20]. Some of these potentials are known to play very important roles in many fields of Physics such as Molecular Physics, Solid State and Chemical Physics [21]. When a particle is in a strong potential field, the relativistic effects must be considered, leading to the relativistic quantum mechanical description of such a particle [22-26]. In the relativistic limit, the particle’s motions are very often described using either the Klien-Gordon (KG) equation or the Dirac equation depending on the spin character of the particle [23,24]. The spin-zero particles like the mesons are satisfactorily described by the KG equation while the spin-half particles such as the electrons are described by the Dirac equation. It is therefore of interest in nuclear and high energy physics to obtain exact solutions of the KG and Dirac equations.

The purpose of the present work is to present the solution of the Alhaidari formalism of the Dirac equation [25] with the gravitational plus exponential potential (GEP) of the form:

(1)

where is the displacement, is the momentum, is the mass, is gravitational acceleration and δ is an adjustable parameter. The GEP could be used to calculate the energy of a body falling under gravity from quantum mechanical point of view. Berberan-Santos et al. [22] have studied the motion of a particle in a gravitational field using the GEP without the exponential term. They obtained the classical and quantum mechanical position probability distribution function for the particle. Also quite recently, Ita and Ikeuba [27] have obtained the bound state solutions of the Klein-Gordon equation for the GEP using the parametric NU method. However, not much has been achieved in the area of solving the Dirac equation with GEP in the literature.

2. The Dirac Equation

The Dirac equation for the lower and upper spinor components can be written as [25]:

(2)

where is the rest mass, is the relativistic energy, and is the vector potential.

(3)

where and is a real parameter. The “” designate the upper and lower components respectively.

3. The Nikiforov-Uvarov Method

The Nikiforov-Uvarov (NU) method is based on the solutions of a generalized second-order linear differential equation with special orthogonal functions [28]. The Schrodinger equation of the type as:

(4)

can be solved by this method. This can be done by transforming Equation (2) into an equation of hypergeometric type with appropriate coordinate transformation to get

(5)

To find the exact solution to Equation (3), we write as

. (6)

Substitution of Equation (6) into Equation (5) yields Equation (7) of hypergeometric type as

(7)

In Equation (6), the wave function is defined as the logarithmic derivative [29]

(8)

with being at most first order polynomials. Also, the hypergeometric-type functions in Equation (7) for a fixed integer is given by the Rodrigue relation as

(9)

where is the normalization constant and the weight function must satisfy the condition

(10)

with

(11)

In order to accomplish the condition imposed on the weight function it is necessary that the polynomial be equal to zero at some point of an interval and its derivative at this interval at will be negative [30]. That is

(12)

The function and the parameter required for the NU method are then defined as [31]

. (13)

(14)

The values in Equation (13) are possible to evaluate if the expression under the square-root be square of polynomials. This is possible if and only if its discriminant is zero. Therefore, the new eigenvalue equation becomes [29]

(15)

A comparison between Equations (14) and (15) yields the energy eigenvalues.

Secondly, the parametric generalization of the NU method is expressed by the generalized hypergeometric-type equation [32]

(16)

Equation (16) is solved by comparing it with Equation (5) and the following polynomials are obtained:

(17)

Now, substituting Equation (17) into Equation (13) gives

(18)

where

(19)

The resulting value of in Equation (18) is obtained from the condition that the function under the square-root should be square of a polynomial and we get

(20)

where

(21)

The new for becomes

(22)

value becomes

. (23)

Using Equation (11), we obtain

(24)

The physical condition for the bound state solution is and thus

(25)

With the aid of Equations (12) and (13), we obtain the energy equation as

(26)

The weight function is obtained from Equation (10) as

(27)

And together with Equation (9), we have

(28)

where

(29)

are the Jacobi polynomials. The second part of the wave function is obtained from Equation (6) as

(30)

where

. (31)

Thus the total wave function becomes

(32)

where N_n is the normalization constant.

4. Solutions of the Dirac Equation

The potential in Equation (1) can be written as

. (33)

where. We can also write Equation (33) as

. (34)

On arranging Equation (34) we get our working potential as

. (35)

The potential of Equation (35) can be used to solve various quantum mechanical equations including the Schrodinger equation (SE), Klein-Gordon equation (KG) and Dirac equation using the NU method for their exact solutions. Writing Equation (32) with the GEP we get

. (36)

Ignoring all terms of the form with in Equation (36) as these will not affect the physics of the calculations, we write Equation (36) as

(37)

where we have used and transformation in Equation (36).

Comparing Equation (37) with Equation (16) yields the following parameters

(38)

Other coefficients are determined as

(39)

From Equation (16)

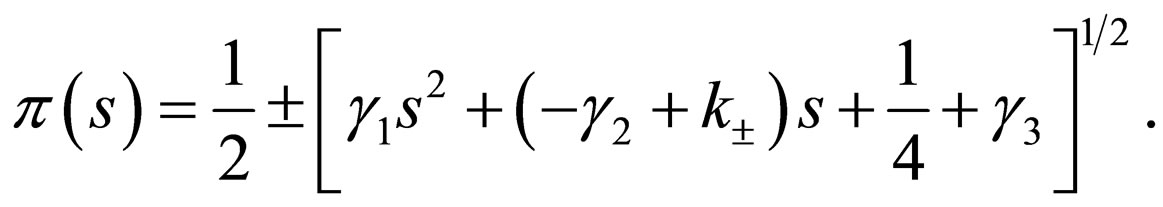(40)

From Equation (18)

. (41)

From Equation (22)

. (42)

The negative derivative of Equation (42) then becomes

. (43)

The new for the NU method is chosen as

. (44)

For

. (45)

Now using Equations (24), (38) and (39) we obtain the energy spectrum of the GEP as

(46)

where

(47)

(48)

. (49)

The weight function is obtained from Equation (25) and the parameters of Equation (39) as

(50)

and using Equation (26) we get the wavefunction χ_n(s) as

(51)

where and is the Laguerre polynomial. From Equation (28) the wave function is

. (52)

The unnormalized wave function is then obtained from Equation (30) as

(53)

where is the normalization constant.

In addition, the corresponding lower-spinor wave function is

. (54)

5. Conclusion

In summary, we have obtained the energy eigenvalues and the corresponding un-normalized wavefunction using the parametric NU method for the Dirac equation with the gravitational plus exponential potential.

6. Acknowledgements

The authors wish to acknowledge Dr. A. N. Ikot of the Department of Physics, University of Uyo in Nigeria for some useful discussions during the preparation of this paper.

REFERENCES

NOTES

^*Corresponding author.