World Journal of Mechanics
Vol.05 No.05(2015), Article ID:56271,8 pages
10.4236/wjm.2015.55008
A Quaternion Solution of the Motion in a Central Force Field Relative to a Rotating Reference Frame
Ioan-Adrian Ciureanu1, Daniel Condurache2
1Department of Medical Informatics and Biostatistics, University of Medicine and Pharmacy “Gr.T. Popa”, Iasi, Romania
2Department of Theoretical Mechanics, Technical University of Iasi, Iasi, Romania
Email: adrian.ciureanu@umfiasi.ro, daniel.condurache@gmail.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 31 March 2015; accepted 10 May 2015; published 13 May 2015
ABSTRACT
The paper presents a quaternion approach of giving a closed form solution of the motion in a cen- tral force field relative to a rotating reference frame. This new method involves two quaternion operators: the first one transforms the motion from a non-inertial reference frame to a inertial one with a very significant consequence of vanishing all the non-inertial terms (Coriolis and cen- tripetal forces); the second quaternion operator provides the solution of the motion in the non- inertial reference frame by applying it to the solution in the inertial reference frame. This process will govern the inverse transformation of the motion and is proved on two particular cases, the Foucault Pendulum and Keplerian motions problems relative to rotating reference frames.
Keywords:
Quaternion, Rotating Reference Frame, Foucault Pendulum Motion, Keplerian Motion

1. Introduction
The present paper presents a quaternion solution of the motion in a central force field relative to a rotating ref- erence frame. It starts from the main Cauchy problem stated below:
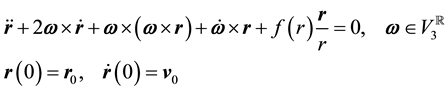 (1.1)
(1.1)
where 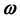 is a differentiable vectorial map and
is a differentiable vectorial map and 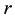 is the magnitude of vector
is the magnitude of vector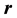 .
.
The quaternion method which will be presented in this paper involves two quaternion operators from which the first one transforms the non-linear with variable coefficients initial value problem (1.1) in another one without the coefficients and the second quaternion operator, applied to the solution of the last problem, will provide the time-explicit closed form solutions for two specific cases, Foucault Pendulum and Keplerian motion problem when 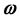 has a fixed direction.
has a fixed direction.
The structure of this paper consists of the following four parts. Section 2 starts with a brief presentation of the quaternion algebra and continues with the presentation of Darboux problem in quaternion form in order to prepare the defining of the quaternion operators.
The next section represents the core of the paper because there the quaternion operators are defined, but not before the transformation in the quaternion form of the Equation (1.1) to be done.
Section 4 proves the accuracy of the method of using quaternion operators for computing the time-explicit closed form solutions for two particular cases, the Foucault Pendulum and Keplerian motions problems in rotating reference frame.
2. Mathematical Preliminaries
2.1. Algebra of Quaternions
The quaternions were invented by William Rowan Hamilton in 1843 [1] . A quaternion can be written as a linear combination:
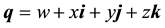 (2.1)
(2.1)
where ,
,  ,
, 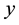 ,
, 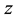 are the constituents of the quaternion and
are the constituents of the quaternion and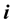 ,
, 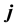 ,
, 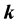 are the imaginary units. The multiplication of two quaternions satisfies the fundamental rules introduced by Hamilton:
are the imaginary units. The multiplication of two quaternions satisfies the fundamental rules introduced by Hamilton:
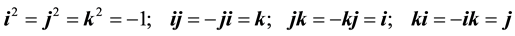 (2.2)
(2.2)
For the quaternion ,
,  is the first constituent and it’s named “the real part” and x, y, z form the vector part of the same quaternion. We can use the quaternions when we need to model rotations, especially in the case of the motion of the rigid body around a fixed point. A quaternion can also be noted as:
is the first constituent and it’s named “the real part” and x, y, z form the vector part of the same quaternion. We can use the quaternions when we need to model rotations, especially in the case of the motion of the rigid body around a fixed point. A quaternion can also be noted as:

where 





The set of quaternions is denoted by 

with 

We already know that an algebra is a vector space where the product may be defined as an additional internal operation. Also, the dimension of an algebra is the algebraic dimension of the vector space. We will define a division algebra as an algebra where the division operation is possible. So, for any 





We will denote with 




when 




We can describe the motion of a particle on a sphere with a constant radius with the help of time-depending quaternions such as:

where 








where 

2.2. Darboux Equation in Quaternion Shape
It is well known that in rigid body kinematics, we need to describe the instantaneous rotation when we know the angular velocity [2] . The common solution is to use the Riccati differential equation which describes the instantaneous rotation of a rigid body when the instantaneous angular velocity is given [3] .
If R is the rotation matrix, the rotation with angular velocity 


If a vector 


and if the matrix 


the instantaneous angular velocity vector 

The rotation matrix that models the rotation with a given instantaneous angular velocity 

where 


The rotation matrix 


Consider 




From Equation (2.14), it results that:

and using vector quaternions property (2.7) we will rewrite (2.18) as

Due to the fact that 



where 


Using (2.15) and the expression of 


3. The Solutions of the Motion in a Central Force Field Relative to a Rotating Reference Frame
In order to find the solutions of the equations specific to the motions in a central force field relative to a rotating reference frame, two reciprocal transformations will be done: first, the motion in the non-inertial reference frame will be transformed in a inertial one through the quaternion operator


Quaternionic Operator
In this section, a quaternion operator 

Knowing that 




and further,

Now, the following quaternion operator 

where 

If
1. For any quaternions 





2. For any quaternions 



3. For any quaternion


4. If 


5. If 


6. 


where 



Theorem 3.1.
The solution of the Cauchy problem:

will be obtained by applying the quaternion operator

Proof. If we apply 

Using the Equation (3.10), it results that:

Replacing 


Consequently, by using the quaternion operator


In the next sections will be studied two particular cases of motions in central force field: the Foucault Pendulum and the Kepler’s motions relative to a rotating reference frame problems.
4. Study of Particular Cases: Foucault Pendulum and Keplerian Motion Problems in Rotating Reference Frames
This section presents the methods adequate to the very known two topics: the Foucault Pendulum and Keplerian motion problems relative to a rotating reference frame problems. In order to achieve the goal of this paper, the motion in central force field Equation (1.1) will be particularized for these two specific cases giving for each of them the characteristic eqaution of 

4.1. Foucault Pendulum Problem
The Foucault Pendulum motion is described by the below initial value problem which is a particular form of the Equation (1.1) that coresponds to a spatial harmonic oscillator relative to a rotating reference frame, with


where 


Applying the quaternion operator

The Equation (4.2) models the spatial harmonic oscillator and it’s solution is:

Due to the Theorem 3.1., the solution of the initial value problem

results from applying the the quaternion operator 

The solution of Equation (4.5) coresponds to a harmonic planar oscillation (with 

In order to compute the closed form solutions of Equation (4.1), we must recall that we’ve assumed that the direction of the vector 






with
If we’ll note:

than the Equation (4.6) can be rewritten as following:

In conclusion, when the direction of the vector 

4.2. Kepler’s Problem in Rotating Reference Frame
The Keplerian motion in a rotating reference frame that rotates with the angular velocity 
following linear initial value problem which is a particular form of the Equation (3.1) with

where 


It was proved in the second section that the solution to the Cauchy problem is obtained by applying the quaternion operator 

The Equation (4.10) describes a typical Keplerian motionunder certain conditions.
In the particular case of negative specific energy, the solution of (4.11) is: [6] [7]

where
In the Equation (4.11), the coefficients 





where the specific energy is noted with 

and the specific angular momentum of the inertial trajectory is noted with 

The eccentricity of the trajectory is given by:

with

and the mean motion is:

where
The function 

with 

Now, in order to find the solution to the Cuchy problem ( 4.21), the quaternion operator 

Using the properties of the quaternion operator

Again, the direction of the vector 






with
Consequenly, similar to the Foucault pendulum case, the Keplerian motion relative to a rotating reference frame consists of two motions: a Keplerian elliptical motion described by the Equation (4.11) and a rotation with the angular velocity
5. Conclusion
The quaternion method described in this work presents a new perspective to the clasical problem of motion in central force field relative to the rotating reference frames and provides us a very powerfull tool to solve the similar problems. Throughout the paper, two quaternion operators are defined in order to reveal the closed form solution to the two particular problems of the Foucault Pendulum and Keplerian motions in rotating reference frame.
References
- Hamilton, W.R. (2000) On Quaternions, or on a New System of Imaginaries in Algebra. The London, Edinburgh and Dublin Philosophical Magazine and Journal of Science, Vols. xxv-xxxvi, No. 3rd Series, 92 p.
- Darboux, G. (1887) Leçons sur la théorie générale des surfaces et les applications géométriques du calcul infinitésimal. Gauthier-Villars, Paris.
- Condurache, D. and Martinusi, V. (2010) Quaternionic Exact Solution to the Relative Orbital Motion Problem. Journal of Guidance, Control, and Dynamics, 33, 1035-1047. http://dx.doi.org/10.2514/1.47782
- Angeles, J. (1988) Rational Kinematics. (Springer Tracts in Natural Philosophy, Vol. 34). Springer-Verlag, New York.
- Condurache, D. and Martinusi, V. (2008) Foucault Pendulum-Like Problems: A Tensorial Approach. International Journal of Non-Linear Mechanics, 43, 743-760. http://dx.doi.org/10.1016/j.ijnonlinmec.2008.03.009
- Condurache, D. and Martinusi, V. (2007) Kepler’s Problem in Rotating Reference Frames; Part 1: Prime Integrals, Vectorial Regularization. Journal of Guidance, Control and Dynamics, 30, 192-200. http://dx.doi.org/10.2514/1.20466
- Condurache, D. and Martinusi, V. (2007) A Complete Closed Form Vectorial Solution to the Kepler Problem. Meccanica, 42, 465-476. http://dx.doi.org/10.1007/s11012-007-9065-7



