ABSTRACT

Dissipative soliton resonance (DSR) is a phenomenon where the energy of a soliton in a dissipative system increases without limit at certain values of the system parameters. Using the method of collective variable approach, we have found an approximate relation between the parameters of the normalized complex cubic-quintic Ginzburg-Landau equation where the resonance manifests itself. Comparisons between the results obtained by collective variable approach, and those obtained by the method of moments show good qualitative agreement. This choice also helps to see the influence of the active terms on the resonance curve, so can be very useful in constructing passively mode-locked laser that generate solitons with the highest possible energies.

Keywords:

High-Energy Pulses, Dissipative Soliton Resonance, Mode-Locked Laser, Fiber Laser, Resonance Curve, Active Terms, Complex Cubic-Quintic Ginzburg-Landau Equation

1. Introduction

One of the most perceptible features of solitons in dissipative systems is that they exist only when there is a continuous energy supply from an external source. Dissipative solitons have an internal energy exchange mechanism [1] , whenever the energy supply is stopped, they “stop living”. This energy has to be dissipated in the medium where solitons are found. Thereby, their formation and stability require a double balance: between the energy supplied and lost on the one hand and between dispersive and nonlinear conservative effects on the other hand. More specifically, their existence depends very deeply on the mutual interaction of losses, nonlinear Kerr effects, gain and dispersion.

The dynamic and stability of dissipative soliton are governed by parameters fluctuations and noise, which can lead to the formation of complex structures like stationary, pulsating solutions [2] .

More specifically, the shape, amplitude, width and all other parameters of dissipative soliton and its energy are defined in advance by the initial conditions and the equation parameters. Nevertheless, the profile of these structures is indeed fixed for a given set of parameters, but one can obtain a wide range of dissipative solitons profiles by tuning each equation parameter.

It has recently been demonstrated that for certain values of the system parameters, the dissipative soliton energy can increase indefinitely and so the process resembles the resonance phenomenon in the theory of oscillators. In such specific situation, the solitons increase their width indefinitely while keeping their amplitude constant. This feature of dissipative soliton was labeled “dissipative soliton resonance”.

These main features of that localized structures offer highly desirable properties for applications, such as the generation of stable trains of laser pulses by mode-locked cavities, or the in-line regeneration of optical data streams [3] .

One of the master equations for wave dynamic in dissipative nonlinear media can be based on a cubic-quintic complex Ginzburg-Landau equation (CGLE) [4] [5] . Also, it was shown numerically that the energy of the dissipative solitons of the cubic-quintic complex Ginzburg-Landau (CGLE) increases significantly when its parameters are located on a special line in the space of parameters [6] . The CGLE has been widely used in nonlinear dissipative optics, due to the clear physical meaning of all its terms in any particular application. Among the important applications are passively mode-locked laser systems and optical transmission lines.

In recent past, Chang et al. have also predicted a novel soliton formation, dissipative-soliton-resonance, in the frame of CGLE [7] [8] . In the reference [7] , they found the resonance approximately by using technique called the method of moments (trial function technique). As it seems impossible to find analytical solutions of the CGLE except for specific values of its parameters [2] , then the same holds true to find the dissipative-soliton-resonance (DSR) parameters using direct analytic technique, to the best of our knowledge.

Indeed, finding the solutions of the CGLE or the region of parameters where DSR exists for a given set of parameters and a given initial conditions is an extremely lengthy and costly task. It requires an enormous number of numerical simulations. In this context, it is helpful to develop theoretical tools that can perceive CGLE soliton solutions more efficiently. In the case of DSR, this task can be simplified with approximations of the pulse shape, finding the set of parameters which predicts the areas where resonances can be found.

In this present study, we devoted, in Section 2 to find the resonance curve by applying the collective variable approach and then we compare our result to the reference [7] where they use the method of moments. In the Section 3 the effects of dissipative terms of the complex cubic-quintic Ginzburg-Landau equation on the resonance curve are intensively study. Finally, in the Section 4 we conclude after the discussion of the result.

2. Resonance Curve from a Collective Variable Approach

We consider, as in the work [7] , the pulse in a system modeled by the complex cubic-quintic Ginzburg-Landau equation. This is in agreement with recent experimental observations of high-energy pulses from passively mode locked lasers, both fiber [9] [10] and solid-state ones [11] . The design of each of these lasers requires specific modeling and numerical simulations [12] [13] . This is tedious procedure. Also, as noted the DSR effect has predictive features, ideally, it can be used to design laser systems for the generation of high-energy pulses. This problem is highly complicated because it requires the use of several equations. One possibility, to certain extent, is to use the master equation approach to simplify this work. This procedure allows us to find the critical parameters of the system that will generate the pulse with the highest possible energy. It is also help to describe any particular laser model. The normalized propagation equation reads:

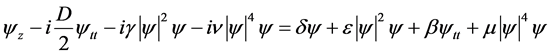(1)

The left-hand-side contains the conservative terms which describe gain and loss of the pulse in the cavity and the right-hand-side includes all dissipative terms. The optical envelope is a complex function of two real variables, where is the retarded time in the frame moving with the pulse, is the propagation distance or the cavity round-trip number. 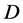accounts for the dispersion, being positive (negative), in the anomalous (normal) dispersion regime. The dispersion is responsible for the net dispersion in the cavity while the saturation coefficient of the Kerr nonlinearity, describes the active part of the reactive nonlinearity. is the Kerr nonlinearity coefficient. The coefficients 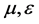and 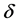are mainly determined by the gain in the system, cavity losses, and transmission characteristics of the mode-locking device while 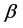roughly describes the main part of the spectral response of the cavity. Higher-order dissipative terms are responsible for the nonlinear transmission characteristics of the cavity, which allows, for example, passive mode locking. This equation admits stationary [14] pulsating [15] and many other types of soliton solutions [16] . Thus, transitions between them occur in the form of sequences of bifurcations [2] [15] . Finding and classification of the different types of CGLE’s solutions are not easy. In [2] we have demonstrated the relevance of the collective variable method for a systematic search of stability domains for different types of solitons in the system leading by CGLE. As well, we use the same approach to draw where resonances can be found; leading to a dramatic reduction of the computation time and later we compare these results with those obtained by the method of moment in the reference [7] .

As in these works [2] [14] [15] , we are dealing with the Collective variable theory [17] , with the same way we decompose the field 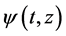in the following way:

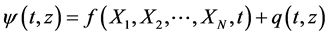
The function 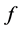named the trial function is a function of the collective variable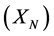, and the excitations in the system (noise, radiation, dressing field, etc.) are represented by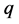. Here one can make an approximation that the exact pulse field propagation can be completely characterized by the trial function. This approximation of neglecting the residual 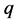field is called the bare approximation [17] . At this stage the precise choice of the trial function which introduces the collective variable is very important.

As in the example in [7] we have chosen the following higher-order Gaussian function:

(2)

where is the soliton amplitude, 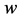is the soliton width, is the soliton chirp, and is the global phase that evolves along with propagation.

The collective variables are variables that evolve along the propagation direction.

Applying the bare approximation by setting the residual field to zero

() to the CGLE namely substituting the pulse field by a given trial function and projecting the resulting equations in the direction [17] of

(3)

we get easily the four collective variables evolve according to the following set of four coupled ordinary differential equations. It gives the dynamical system for the evolution of the soliton amplitude, width, quadratic chirp coefficient and its global phase.

(4)

The main advantage of the trial function lies in its simplicity, which makes the procedure of derivation of the variational equations relatively easy. Thus it allows seeing clearly the influence of each parameters of the CGLE on the various physical parameters of the soliton. To a certain extent the natural control parameter of the soliton is the total energy, and one of the key benefit of the collective variables approach is that the total energy can also expressed as function of the trial function parameters. Here it is interesting to gain insight from this simple and useful quantity, which is defined as:

(5)

Likewise the energy density can expressed as function of soliton parameters:

(6)

And the corresponding flux, is given by:

(7)

Then the evolution equations (Equation (4)) for the soliton parameters can also be expressed as a function of the total energy as following:

(8)

Here the master equation (Equation (1)) is reduced to an ordinary differential equation given by the soliton energy, width and quadratic chirp coefficient. These differential equations are expressed as in term of the energy and are in good agreement to those found by the method of moments (see Equation (7) in [7] ). There are the same terms in both variational equations, and the energy evolves identically in both cases. But the coefficients of the chirp propagation differ slightly from the Equation (8), probably due to the added phase constant.

The results clearly confirm that the collective variable approach is a useful tool for studying the dynamic of the soliton evolution. It also helps to research the resonance curve analytically. We know that near the resonance curve, that soliton energy, its width and the quadratic chirp coefficient.

So the terms in Equation (8) of the order of and are close to zero and can be neglected (see details in [7] Appendix B). Consequently, the ordinary differential equation Equation (8) is then simplified and becomes:

(9)

It is recognised that near the resonance curve the fixed points are defined by the zeros of the right-hand side of the equation presented above. As well as the values end tend to approach constants with being negative. So solving the first two equations in Equation (9) relative end we obtain:

where,

Substituting these equations into the third equation in Equation (9), we obtain the expression for the resonance curve in terms of the system parameters

(10)

The expression Equation (10) depends on all coefficients of the propagation equation Equation (1). It has the same terms as that found by the method of moments (see Equation (10) in [7] ). Thanks to collective variable approach, we have found a simple analytic expression for the resonance curve which is in good qualitative agreement with in [7] . Below, in the plane of parameters and, we plot the resonance curve obtained by the collective variable approach (solid line) and the method of moments (dash line). The solid one is in reasonably good qualitative agreement with the other one. According for the chosen values of the CGLE (see inside the Figure 1), the resonance curve appears for negative and positive. When and are small the curve tends to a relative constant value. However, when the same parameters increase, the resonance curve rises quickly and its slope tends almost to zero. Near these curve the soliton energy and width increase to infinitely large values.

3. Influence of Dissipative Terms on Dissipative Curve

The design of a particular laser with specific features requires numerous modeling

and numerical simulations [18] [19] . So, as the dissipative soliton resonance effect of CGLE has predictive, it can be uses to design laser systems for the generation of high-energy pulses. It knows that the physical meaning of each term of CGLE depends on the real problem which must be examined. For instance, as and determine the gain in the system, cavity losses, transmission characteristics of the mode-locking device and the main part of the spectral response of the cavity, they can be suitably chosen for generation of high-energy dissipative solitons. The coefficients of CGLE equation can be determined for each particular laser. These coefficients could be too complex functions of the real laser parameters or very complicated specific design factors. Under these conditions it is important to study the impact of these coefficients on the resonance curve. The role of, the higher-order reactive nonlinearity term has been studied in [20] . In this present study we focus namely on the influence of the dissipative (or active) terms of the CGLE on the resonance curve. The higher-order gain and nonlinearity terms actions on the dissipative resonance curve are summarized on the Figure 2 and Figure 3. The soliton resonance curves in the plane for three values of are shown in Figure 2 and for three values of are shown in Figure 3. For the low values of the dispersion (below −6) regardless of the choice of higher-order reactive nonlinearity term (Figure 2) and the saturation of the nonlinear gain (when negative) (Figure 3) the resonance

curve retains almost the same value. The different curves have the same distinctive features. First, they kept an almost constant value but when the dispersion value is greater than −6 the resonance curves differentiate and increase steadily. In this case the solitons have different amplitudes, widths and therefore energies which basically provide the highest distinguishing features.

The other active term, plays an importance role in the dynamic of dissipative soliton. When it is negative, it means linear loss in the system. The effect of this coefficient on the resonance curve is plot in the Figure 4 for different values. For the chosen values inside the figure, when, whatever the coefficient, the resonance curve stains the same value. For a given set of parameters, each curve begins with different values and allure but when we increase progressively the nonlinear gain, the different curves converge in the same value and evolution. This fact is very important for the design for specific laser. It shows how one can manage this parameter for the desire behavior.

The spectral filtering or gain dispersion (if positive) in the cavity is described by the coefficient. Its action is determining in the study of dissipative solitons and on the pulse profile. As well its influence on the resonance curve in plane is represented in the Figure 5. Depending on the coefficient sign the curve evolves differently. The curves are symmetrical along the vertical axis passing through the origin. For positive values, the resonance curves exist only

when the dispersion is negative. However, for positive dispersion values, the coefficient must be negative to have the resonance curves. Nevertheless, regardless of the sign of the dispersion the curves evolve gradually for low values of, but when the nonlinear gain increases, the resonance curve surge ahead to towards a relatively variable value.

4. Conclusion

Finally, in this present study, we have presented collective variable approach for the phenomenon of dissipative soliton resonance found earlier using numerical simulations and confirmed by the method of moments. In particular, using the method of collective variable approach, we have found an approximate relation between the parameters of the normalized complex cubic-quintic Ginzburg- Landau equation and simple analytic expression for the resonance curve which is in good qualitative agreement with the results of the method of moments. But also as the master equation that describes laser systems has many parameters, it’s so difficult to study the influence of all of them on the soliton properties. Here we describe the influence of dissipative terms of CGLE on resonance curve. Namely how the linear loss, the gain and its saturation in the system and the spectral response of the cavity can be suitably chosen for generation of high-energy pulses. Clearly this work can help to optimize the active parameters of cavities that generate solitons with the highest possible energies. We think that these results can be helpful for the design of the mode-locked laser systems that generate record-high energy short pulses, without the need for additional amplifiers.

Cite this paper

Kamagaté, A., Konaté, A., Soro, P.A. and Asseu, O. (2017) Effects of Dissipative Terms on Dissipative Soliton Resonance Curve. Optics and Photonics Journal, 7, 57-66. https://doi.org/10.4236/opj.2017.73005

References