Boundary Value Problem for an Operator-Differential Riccati Equation in the Hilbert Space on the Interval

O. O. Pokutnyi^*

Institute of Mathematics of NAS of Ukraine, Kiev, Ukraine.

DOI: 10.4236/apm.2015.514081                

Abstract

The paper is devoted to obtaining the necessary and sufficient conditions of the solvability of weakly perturbed boundary-value problems for the nonlinear operator-differential Riccati equation in the Hilbert space on the interval and whole line with parameter ?. We find the solution of the given boundary value problem which for ε = 0 turns in one of the solutions of generating boundary value problem. Solution of the generating problem is constructed with the using generalized operator in analytical form. Iterative process for finding of solutions of weakly nonlinear equation with quadratic error is constructed.

Keywords

Riccati Equation, Hamiltonian System, Generalized Green’s Operator

Received 28 July 2015; accepted 27 December 2015; published 30 December 2015

1. Introduction

Riccati equation plays an important role in the theory of optimal control, physics and many others applications. It should be emphasized that such equations are very often used in the games theory and calculus of variations. It should be noted here that in general, many papers are devoted to obtaining the conditions of the solvability in the regular case. We noted such papers as [1] -[12] where considering equation was investigated in the finite- dimensional and in the infinite-dimensional cases. It should be noted that this equation was investigated as in the operator and matrix form or as in the operator-differential and differential form (see the bibliography).

There are many papers where the matrix Riccati equations and operator-differential Riccati equations were investigated. As a rule, such equations were investigated in the regular case where the given problem had a unique solution. In the nonregular case, such equation was investigated (in the periodic case) in the work of Boichuk O. A. and Krivosheya S. A. [12] . In the paper [4] , the discrete Riccati equation was investigated. In the paper of Pronkin [8] , the question about quasiperiodic solutions of the matrix Riccati equation with coefficients which are Arnold functions is investigated. Dissertation of Christian Wyss [1] is also devoted to the perturbation theory for Hamiltonian operator matrices and Riccati equations in the Hilbert space.

In the present paper, using the technique of generalized inverse operators, we derive a criterion for the solvability of the given problem, generating problem and analyzing the structure of the solution set. We construct the iterative process for finding the solutions of weakly nonlinear problem which is the modification of Newton method and converges with quadratic error.

The article consists of three parts.

The first part of the given paper is devoted to the statement of the problem and denotations.

The second part is devoted to obtaining the necessary and sufficient conditions of the existence of bounded solutions of generating boundary value problem.

The last part is devoted to obtaining the necessary and sufficient conditions of the existence of solutions of weakly nonlinear Riccati operator-differential equation.

In this paper, Riccati equation was investigated in the critical case in the Hilbert space. And we obtain the full theorem of the solvability in linear case.

2. Statement of the Problem

We consider the following boundary value problem

(1)

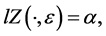(2)

where 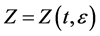is an unknown operator function from the space, and 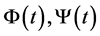are bounded operator-valued functions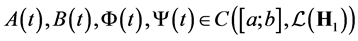; or in another words these operators are the ways in the space of linear and bounded operators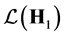, 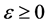is a small parameter. We find the solution 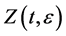of boundary value problem (1), (2) which for 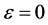turns in one of the solutions of the generating boundary value problem

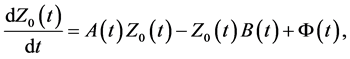(3)

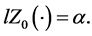(4)

3. A Solvability Criterion and the Structure of the Solution Set of the Nonperturbed Problem

Solutions on the Finite Interval

Consider the case when the differential equation is defined on the finite interval 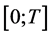or on the infinite inter- val. Let us the operator whose action on the operator-valued function is given by the formula

(5)

where, are evolution operators [13] , of the following operator-differential equations

(6)

(7)

respectively. Obviously, that satisfies the following operator-differential equation

Using the operator, we write out the general solution of the nonperturbed problem

(8)

(9)

in the form

where M is an arbitrary operator and

The main statement of this part is the following theorem.

Theorem 1. Consider the boundary value problem (8), (9).

1) There are exist solutions of the boundary value problem (8), (9) if and only if the following condition is true

(10)

where, and; under this condition the family of solutions have the following form

(11)

is generalized Green’s operator and is Moore-Penrose pseudoinvertible;

2) There are exist generalized solutions of boundary value problem (8), (9) if and only if

where is strong generalized invertible operator. Then the family of solutions of the Equation (8) has the form

(12)

where

is generalized Green’s operator.

3) There are exist the quasisolutions if and only if and in this case we have the solutions in the following form

(13)

with the same generalized invertible.

Sketch of the proof: Substituting in the boundary condition we will have

(14)

and then we obtain the following operator equation

(15)

Using the notion of generalized invertible operator [14] [15] , we have the following variants for the equation:

1) If then Equation (15) has the solution if and only if the following condition is true

(16)

If the condition (16) is satisfied then the set of the solutions of the Equation (15) has the following form:

for any linear and bounded operator C. Then the family of solutions of the boundary value problem (8), (9) has the form

(17)

where

is generalized Green’s operator.

2) If. If the we have the generalized solutions in the following form

if and only if the following relation is hold

where is strong generalized invertible operator [15] . Then the family of solutions of the boundary value problems (8), (9) has the form

(18)

where

is generalized Green’s operator.

3) If the we have the quasisolutions in the form

(19)

with the same generalized invertible (see also the paper [16] ).

4. Weakly Nonlinear Case

4.1. Necessary Condition

Now we consider the boundary value problem (1), (2). We find the solution of the boundary value problem (1), (2) which for turns in one of the solutions of boundary value problem (8), (9). Now we obtain the necessary condition of the existence of such solutions.

Theorem 2. (necessary condition) Let the boundary value problem (1), (2) has the solution which for turns in one of the solution with operator. Then the operator satisfies the following operator equation for generating operators

(20)

Proof. Suppose that the boundary value problem (1), (2) has solution which for turns in one of the solutions with C₀. By virtue of the theorem 1 thefollowing condition of solvability is true

(21)

where

Such as condition (10) is true, then the condition of solvability (21) we can rewrite in the following form

Dividing by and passing to the limit when tends to zero we obtain

or in the form

(22)

From this condition we obtain the theorem 2.

4.2. Sufficient Condition of the Solvability

Now we obtain the sufficient condition of the solvability of boundary value problem (8), (9). We make the change of the variable by the rule. Then we obtain the following boundary value problem

(23)

(24)

The family of solutions of the Equation (23) has the following form

(25)

(26)

under condition (21)

(27)

Substituting in this expression (25) and using the Equation (20), we have

(28)

Then we can rewrite this expression in the following form of the operator equation

(29)

where

(30)

and

(31)

If the following condition

(32)

is true then the equation (30) has the solution

(33)

Under condition (32), we can prove that boundary value problem (23), (24) have solutions. In a such way, we prove the following theorem.

Theorem 3. (sufficient condition) Under condition (32) boundary value problem (23), (24) is solvable. Solution of the given boundary problem can be found with using the following converging iterative process

(34)

(35)

(36)

with zero initial data.

Proof.

Proof of this theorem uses the modification of the fixed point theorem and is performed as well as the proof of the theorem 3 from the paper [17] .

Example 1.

Considering the following boundary value problem with the matrix-valued in l₂ functions,

(37)

nonhomogenous part has the following form

(38)

and conditions on infinity

(39)

In this case

(40)

(41)

Operator has the following form

(42)

with *-star matrix which has the following form

(43)

(44)

In this case, the operator has the following form

(45)

From the condition (39) we obtain that, etc. and, etc. we can take arbitrary.

In the such way, we have

(46)

The unperturbed problem has the following form

(47)

(48)

Consider the following problem with the matrix,

(49)

nonhomogenous part has the following form

(50)

In this case

(51)

where

(52)

where

(53)

Here are and characteristic numbers of the block of the Fibonacci matrix B.

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Wyss, C. (2008) Perturbation Theory for Hamiltonian Operator Matrices and Riccati Equations. Dissertation, Bern, 164 p.
[2]	Abbasbandy, S. (2006) Iterated He’s Homotopy Perturbation Method for Quadratic Riccati Differential Equation. Applied Mathematics and Computation, 175, 581-589. http://dx.doi.org/10.1016/j.amc.2005.07.035
[3]	Sragovich, V.G. and Chornik, (1995) About Asymptotical Behavior of Solutions of Algebraic Riccati Equation for Continuous Time. Automation and Remote Control, No. 8, 90-92.
[4]	Lazareva, A.B. and Pakshin, P.V. (1986) Solution of Matrix Lurier, Riccati and Lyapunov Equations for Digital Systems. Automation and Remote Control, No. 12, 17-22.
[5]	Chu, E.K.-W., Fan, H.-Y. and Lin, W.-W. (2005) A Structure-Preserving Doubling Algorithm for Continuous-Time Algebraic Riccati Equations. Linear Algebra and Its Applications, 396, 55-80. http://dx.doi.org/10.1016/j.laa.2004.10.010
[6]	Freiling, G. (2002) A Survey of Nonsymmetric Riccati Equations. Linear Algebra and Its Applications, 351-352, 243-270. http://dx.doi.org/10.1016/S0024-3795(01)00534-1
[7]	Hiramoto, K., Doki, H. and Obinata, G. (2000) Optimal Sensor/Actuator Placement for Active Vibration Control Using Explicit Solution of Algebraic Riccati Equation. Journal of Sound and Vibration, 229, 1057-1075. http://dx.doi.org/10.1006/jsvi.1999.2530
[8]	Pron’kin, V.S. (1994) On Quasiperiodic Solutions of the Matrix Riccati Equation. Russian Academy of Sciences, Izvestiya Mathematics, 43, 455-470. http://dx.doi.org/10.1070/im1994v043n03abeh001575
[9]	Osmolovskii, N.P. and Lempio, F. (2000) Jacobi Conditions and the Riccati Equation for a Broken Extremal. Journal of Mathematical Sciences, 100, 2572-2592. http://dx.doi.org/10.1007/BF02673843
[10]	Grigoryan, G.A. (2015) Global Solvability of Scalar Riccati Equations. Russian Mathematics (Izvestiya VUZ. Matematika), 59, 31-42.
[11]	Boichuk, O.A. and Krivosheya, S.A. (1998) Criterion of the Solvability of Matrix Lyapunov Type Equations. Ukrainian Mathematical Journal, 50, 1021-1026. http://dx.doi.org/10.1007/BF02513089
[12]	Boichuk, A.A. and Krivosheya, S.A. (2001) A Critical Periodic Boundary-Value Problem for a Matrix Riccati Equation. Differential Equations, 37, 464-471. http://dx.doi.org/10.1023/A:1019267220924
[13]	Krein, M.G. (1970) Stability of Solutions of Differential Equations in Banach Space. Science, Moscow, 534 p. (In Russian)
[14]	Boichuk, A.A. and Samoilenko, A.M. (2004) Generalized Inverse Operators and Fredholm Boundary-Value Problems. VSP, Utrecht-Boston, 317 p. http://dx.doi.org/10.1515/9783110944679
[15]	Pokutnyi, O.O. (2013) Generalized-Invertible Operator in the Banach Hilbert and Frechet Spaces. Visnik of the Kiev National Taras Shevchenko University, Series of Physical and Mathematical Sciences.
[16]	Panasenko, E.V. and Pokutnyi, O.O. (2013) Boundary Value Problems for Differential Equations in Banach Space with Unbounded Operator in Linear Part. Nonlinear Oscillations, 16, 518-526.
[17]	Pokutnyi, A.A. (2012) Bounded Solutions of Linear and Weakly Nonlinear Differential Equations in Banach Space with Unbounded Linear Part. Differential Equations, 48, 803-813. http://dx.doi.org/10.1134/S0012266112060055