Utilizing Dimensional Analysis with Observed Data to Determine the Significance of Hydrodynamic Solutions in Coastal Hydrology ()
1. Introduction
Surface-water modeling is an important tool to support many types of hydrologic investigations. As is generally the case in modeling, it allows the prediction of future conditions and investigation of causative factors. Surface- water models offer a variety of formulas to represent flow and water level. Formulas that make simplifying as- sumptions by neglecting certain terms provide for solutions requiring fewer calculations and often require less parameterization. Hydrodynamic flow governing equations account for spatial and temporal changes in mo- mentum, whereas simpler formulations retain only the frictional and gravitational forcing terms or combine an empirical flow relationship with mass conservation. Generic criteria are used to determine the formula appropriate for a specific hydrologic situation. For example, a location with dominant tidal fluctuations requires the full hy- drodynamic equations whereas a steadily flowing mountain stream can be represented without the inertial terms. But for more complex and diverse conditions, it is difficult to develop the insight and details required to choose a formula without a thorough examination of the terms in the numerical formulation and how they relate to actual flow conditions.
Comparisons between different surface-water flow formulations have usually relied on simulation results only or comparisons of model results to field water levels or discharge values. Reference [1] compared a level-pool reservoir routing model to a Muskingum-Cunge river-routing model by using output from the hydrodynamic DAMBRK model as criteria for comparison. The hydrologic conditions under which each of the two modeling methods incurs the most errors relative to DAMBRK were identified. Reference [2] examined the parameteriza- tion of differing formulations to identify the mathematical advantages and disadvantages. This approach does not give a direct quantification of the errors induced in each method, but does offer guidelines to each formulation’s limitations.
Field data are almost always used for model comparison and verification, as the purpose of any model is to represent a physical system. Basic parameters of the model output, such as water level, discharge, and constituent concentrations, are compared between the model output and data measured in the field. However, substantially more information can be derived from the field data than a simple comparison of values. Statistics are often de- rived from field data, lending insight into the system’s behavior. Furthermore, sufficient field data exist in many locations to compute the individual mathematical terms in the surface-water flow equations and find their relative magnitude, yielding insight into what formulation is appropriate for a particular situation.
This paper describes an effort to parameterize the flow conditions under which inertial terms are important and are needed in surface-water flow computations. The importance of the inertial terms in surface-water flow com- putations is analyzed through: 1) computation of surface-water flow equation terms from field data; 2) formulation of parameters that incorporate dimensionless numbers to represent the significance of the inertial terms; and 3) comparison of test-case model simulations with and without inertial terms. Two field sites are used for com- parison, a natural river in a tidal environment and a structure-managed coastal canal. The results of the analyses demonstrate the importance of the inertial terms and the conditions in which a full hydrodynamic solution is needed.
2. Formulations
The different surface-water flow formulations can be categorized according to complexity, that is, how many of the terms in the conservation equations of mass and momentum are included. Terms that are small relative to the predominant terms can be neglected, allowing for simpler formulations and solution schemes.
The governing hydrodynamic flow equations in one dimension [3] , with a momentum coefficient equal to one and neglecting lateral inflows and wind shear, take the form:
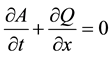(1)
(A) (B) (C) (D)
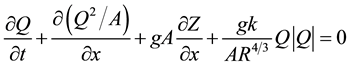(2)
temporal spatial gravity friction
where, Q is discharge, t is time, A is cross-sectional area, x is distance, g is gravitational acceleration, Z is stage, k is the friction coefficient, and R is hydraulic radius (area divided by wetted perimeter). The friction coefficient k is Mannings n squared in SI units or Mannings n squared divided by 2.208 in English units. Equation (1) ex- presses conservation of mass and Equation (2) expresses conservation of momentum.
Each term on the left-hand side of Equation (2) expresses a force or a change in momentum. Term A is the change in momentum from temporal acceleration. Term B is the change in momentum from spatial acceleration. Term C is the gravity force and Term D is the force due to friction. The sum of the forces and change in mo- mentum equal zero.
If the temporal acceleration term is removed from Equation (2), it represents flow that is steady in time but varies gradually in space. If both the temporal acceleration and spatial acceleration terms are removed, Equation (2) represents steady, uniform flow and it reduces to a simple, Mannings-based, equation for flow [4] :
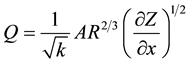(3)
Equation (3) can be combined with the continuity equation (Equation (1)) to form the diffusion analogy equa- tion. When rearranged in terms of the dependent variable Q, this equation resembles the classic diffusion equation in mathematics [5] . However, another variation involves computing the Q value with Equation (3) and using this value in Equation (1). This is the diffusion-analogy formulation that will be discussed and contrasted to the full hydrodynamic Equations (1) and (2) in this paper.
The ability to evaluate the effects of the inertial (acceleration) terms without resorting to the complex solution of Equations (1) and (2) is of considerable interest. Reference [6] developed linear analogs of the inertial terms for the diffusion-analogy formulation. The formulation defined the inertial effects in terms of the Froude Number and the hydraulic diffusivity. The linearized form is a parabolic analog to the hyperbolic equation, so only one wave propagation direction is possible. However, the study indicated that including just one of either of the inertial terms is worse than neglecting both terms [6] so the relative magnitudes of the terms were considered in our work. Also, the study indicated that the Froude Number can be used to indicate the magnitude of the hydrodynamic effects. Another study to examine simplified overland flow equations developed dimensionless forms of the in- ertial terms to determine the effectiveness of the kinematic wave and diffusion analogy formulations [7] . The kinematic wave is similar to the diffusion analogy except that the water slope term ∂Z/∂x in Equation (3) is re- placed by the bed slope. The analysis examined the magnitude of the temporal and spatial acceleration terms in response to rainstorms using a one-dimensional numerical model. It was found that in order for the kinematic wave approximation to be appropriate, a larger Froude Number, over 0.5, is necessary. The temporal acceleration was found to exceed the spatial acceleration in the cases examined. Reference [8] also developed criteria for use of the diffusive analogy in terms of the Froude Number and the kinematic wave number. Limits on the accurate use of the diffusive analogy were developed through a numerical solution. These analyses yield useful insight but do not utilize the wealth of field data available to examine hydrodynamic phenomena.
One use of Froude-Number-based parameters is to determine when the full hydrodynamic equation should be used instead of the diffusion analogy in a numerical model. Such a parameter is derived below and comparisons to field data and numerical model results are shown.
2.1. Computer Models
Both the full hydrodynamic formulation and the diffusion-analogy formulation are used by many numerical model applications. Commonly, models designed for estuaries and coastal rivers use the full hydrodynamic formulation. This includes one-dimensional models such as BRANCH [9] and UNET [10] , two-dimensional models such as RMA2 [11] and SWIFT2D [12] , and three-dimensional models such as the Environmental Fluid Dynamics Code [13] and ADCIRC [14] . For applications to many watersheds and inland rivers where flow is less dynamic, dif- fusion-analogy formulations are simpler and easier to solve. These applications include one-dimensional models such as DAFLOW [15] and two-dimensional applications as in the South Florida Water Management Model [16] . The choice of model to apply to a given situation is often intuitively determined, and based on the user’s judgment as to the behavior of the hydrologic system and the parameters of interest.
Many of these hydrodynamic and diffusion analogy models are used while coupled to a groundwater model [17] - [20] . The coupling of the SWIFT2D two-dimensional hydrodynamic flow and transport model to the three- dimensional SEAWAT groundwater model is referred to as the Flow and Transport in a Linked Overland/Aquifer Density-Dependent System (FTLOADDS). SEAWAT is the variable-density transport version of the commonly used groundwater flow model MODFLOW [21] . SEAWAT has been applied to several areas in South Florida to investigate coastal estuarine flow, salinity and heat transport, and groundwater and surface-water interactions [22] - [24] . Another tool under development for application in South Florida is the SWR1 package for MODFLOW [25] . SWR1 represents one- and two-dimensional surface-water flow using a simple-routing or the diffusion analogy method. The primary motivation for the development of SWR1 is to represent the heavily managed canal network and structures that have been constructed throughout the southeast coast of Florida.
TheSWIFT2D model, imbedded in FTLOADDS, was used to compare the hydrodynamic and diffusion analogy methods. Simulations of the same scenario are run with the fully hydrodynamic formula and also with the inertial terms (A and B in Equation (2)) removed. Without the hydrodynamic terms, the solution resembles the SWR1 diffusion analogy method. A two-dimensional test problem was used to simulate a rainfall event dissipating in a shallow-water environment. A range of frictional resistance and mean flow values were used to assess the mag- nitude of the hydrodynamic effects on flow velocity, discharge, and stage. The SWIFT2D model with and without inertial terms was also applied to one of the field site conditions.
2.2. Field Computation of Hydrodynamic Terms
In order to examine the magnitude of the component terms in the hydrodynamic flow Equation (2), continuous stage and discharge data were used from two sites in South Florida. Each site had two measurement stations, al- lowing the computation of the water level slope and the spatial changes in discharge. The two stations on the North River, southwest coast of Whitewater Bay, are located about 2550 meters apart and continuously collect stage measurements and acoustically-measured discharge. The Miami Canal site is located upstream of hydraulic con- trol structure S-26 (Figure 1). Stage levels are measured on the upstream side of the S-26 gated spillway, and a station 366 meters upstream from S-26 measures continuous stage and discharge. Fifteen-minute data from Jan- uary 1, 2008-December 31, 2008 were used for the analysis.
The terms in the hydrodynamic flow equation (Equation (2)) can be expressed in finite-difference form to compute their values from the field data. At the North River location, the terms referenced in Equation (2) take the form:
![]()
Figure 1. Location of field data collection sites.
Term A (temporal acceleration) =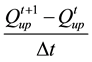 
upstream and 
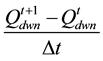downstream;
Term B (spatial acceleration) =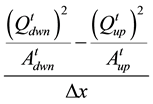
;
Term C (gravity term) =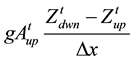 
upstream and 
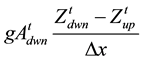downstream;
Term D (friction term) =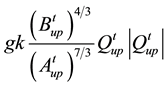 
upstream and 
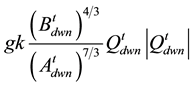downstream.
where Δt is the data-collection time interval (15 minutes), Δx is the spacing between the stations (2550 meters), B is the channel top width (approximating the wetted perimeter), the superscripts indicate the collection time (t is the current time), and the subscripts indicate the station location (upstream or downstream). Note in Table 1 that the temporal and spatial weightings of each term are limited by the available data.
The magnitudes of hydrodynamic equation component terms at North River in 2008, shown in Figure 2, in- dicate that the gravity component achieves the largest magnitudes, both positive and negative. The magnitudes of all terms tend to be larger at the downstream location where the cross section is larger. The inertial terms are smaller; the mean absolute value of the temporal acceleration term is 4.2 percent of the gravity term upstream and 9.2 percent of the gravity term downstream. The temporal acceleration term is consistently larger than the spatial acceleration term, as were the findings in [7] . More importantly, the temporal acceleration term is occasionally larger in magnitude than the gravity term, 3.7 percent of the time upstream and 7.0 percent of the time downstream. These are times when flows are changing fastest, such as tidal reversals, when the gravity term is low due to the flat slope. The spatial acceleration term is smaller with a mean absolute value 2.8 percent of the gravity term.
The analysis of the North River data indicates that the inertial terms can be important in their absolute magni- tude and percent of time they dominate. North River is in a coastal environment with a tidal signature and is fed at its upstream end from the Shark Slough (Figure 1). A seasonal cycle is visible with higher values and more va- riability between June and November. Summer and fall are the wet season in South Florida with higher rainfall and flows, so the terms in the momentum equation, especially friction and inertial, are higher. The effects of Tropical Storm Fay when it hit South Florida in mid-August 2008 can be seen in Figure 2, especially in the gravity term. However, the inertial terms did not respond remarkably to Fay, indicating more gradually varying effects.
A somewhat different hydrologic condition exists on the east coast of South Florida where canal conveyance of surface water is highly regulated using control structures. The Miami Canal location (Figure 1) is upstream of the coastal control structure S-26 and is subject to the most rapid transients when the gate on the control structure is operated. The upstream station has both continuous stage and discharge measurements, but the downstream sta- tion only has measured stage, and discharge is estimated based on the gate opening and stages at the gate. The spatial acceleration term cannot be calculated without a downstream discharge measurement. However, temporal acceleration is consistently much larger than spatial acceleration, as seen in the North River analysis and [7] . A decision was made to use the measured upstream discharge and calculate only the upstream values of temporal acceleration (Term A), gravity (Term C), and friction (Term D). In the Miami Canal example, Δt is 15 minutes and Δx is 366 meters.
The magnitude of each term for the 2008 time series at Miami Canal, shown in Figure 3, can be compared and contrasted with the North River data in Figure 2. The Miami Canal inertial component remains smaller than at North River for the majority of the time, but peaks occasionally along with the friction term as a result of S-26 gate operations. For the period August through November, the gates are operated more frequently with large flows to drain the excess wet-season rainfall. One interesting phenomena is visible in late March, early April, and to a lesser degree after October. The friction and temporal acceleration component terms are both larger in magnitude than the gravity term when the S-26 gate is opened. Rather than a balance primarily of gravity and friction forces, temporal acceleration and friction occasionally predominate in the Miami Canal, where short-term gate operations create a larger hydrodynamic effect than the tidal fluctuations create at North River. The ratio of the mean absolute values of the temporal acceleration term to the gravity term for Miami Canal is 11.2 percent, somewhat larger than
![]()
Table 1. Temporal and spatial locations of field values used to evaluate terms in Equation (2).
![]()
Figure 2. Computed terms for conservation of momentum at North River stations.
![]()
Figure 3. Computed terms for conservation of momentum at Miami Canal station.
at North River. The water-surface slope in the Miami Canal tends to be very low, reaching no slope when the gate is closed, making the hydrologic conditions conducive to hydrodynamic dominance.
There are two attributes suggesting the Miami Canal is a better site to analyze hydrodynamic effects. Upstream and downstream measurement points at Miami Canal are closer than at North River (366 meters versus 2550 meters) so computed spatial-difference terms are more reliable. Also, the manmade cross section is more uniform at Miami Canal, which better satisfies the assumptions of one-dimensional flow. One reasonable indicator of the analysis reliability is to sum the terms in Equation (2), which should equal zero, and average them over the time period. Another is the standard deviation of the sum of the terms, which indicates how much the sum fluctuates from its mean value. At North River, the mean of the sum of the computed terms is −0.623 × 10−3 cubic meters per second squared, 45.3 percent of the gravity term’s mean value of −1.376 × 10−3 cubic meters per second squared. At Miami Canal, it is assumed that the spatial acceleration term would be negligible enough so that the mean of the sum of the computed terms is representative, yielding a value of 0.195 × 10−3 cubic meters per second squared, which is 8.1 percent of the gravity term’s mean value of −2.415 × 10−3 cubic meters per second squared. This lower discrepancy at Miami Canal is reasonably attributable to its spatially uniform cross section and closer up- stream and downstream stations. The standard deviation of the sum of computed terms is 1.40 × 10−2 cubic meters per second squared for North River and 0.85 × 10−2 cubic meters per second squared for Miami Canal, demon- strating a lower variability for Miami Canal also.
3. Deriving Relationships with the Froude Number
In order to quantify the significance of the component inertial terms, a formula was developed in terms of di- mensionless quantities.
The Froude Number is defined as:
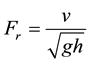(4)
where, v is the flow velocity, g is gravitational acceleration, and h is depth of water. Differentiating the Froude Number squared with respect to time:
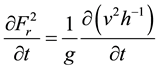(5)
Expanding and multiplying through by v:
![]()
(6)
Dividing by ![]()
yields:
![]()
(7)
The continuity equation (Equation (1)) can be simplified for a unit width of flow and relatively uniform depth as:
![]()
(8)
Combining Equations (7) and (8):
![]()
(9)
Rearranging:
![]()
(10)
Equation (7) can be rearranged to:
![]()
(11)
Combining Equations (10) and (11):
![]()
(12)
where the right-hand side of Equation (12) is the temporal and spatial acceleration (inertial) terms in the mo- mentum equation expressed in terms of velocity v rather than discharge Q as in Equation (2).
A similar approach is taken when differentiating the Froude Number with respect to spatial location x:
![]()
(13)
Expanding and multiplying through by v:
![]()
(14)
Dividing by ![]()
yields:
![]()
(15)
Equation (8), the continuity equation, can be rearranged:
![]()
(16)
Combining Equations (15) and (16):
![]()
(17)
Multiplying through by v and rearranging:
![]()
(18)
Rearranging:
![]()
(19)
Modifying the equation so the right-hand side of the equation is in terms of stage, Z, instead of depth, h:
![]()
(20)
where ε is the bottom bed elevation. A rearrangement yields:
![]()
(21)
As![]()
, the first term in the parentheses can be modified:
![]()
(22)
The right-hand side of Equation (22) is the gravity term in the momentum equation.
3.1. Evaluating Interrelationship of Formulation Terms
The comparison of Equations (12) and (22) can indicate the properties of the dimensionless numbers when inertial terms dominate:
![]()
(23)
Rearranging and transforming this into finite-difference form: the conditions when Equation (12) (inertial terms) is substantially larger than Equation (22) (gravity term) can be expressed:
![]()
(24)
where the absolute value signs indicate that magnitude, not sign, is the important factor. The first term on the left-hand side and the last term on the right-hand side represent the effects of temporal and spatial variations in Froude Number, whereas the last term on the left-hand side and the first term on the right hand side represent the effects of temporal variations in depth and the channel slope Δε/Δx. This can be visualized as two sets of rela- tionships, dependent on each other, one dealing with the temporal and spatial change in the Froude Number squared:
![]()
(25)
and the other with the relationship of temporal depth changes to the bottom slope:
![]()
(26)
Equations (25) and (26) cannot be considered independent of each other, but they do give a framework to define important quantities. Equation (25) includes![]()
, ![]()
, and ![]()
and Equation (26) includes, ![]()
, ![]()
, and![]()
. The channel slope ![]()
is a constant for a given location, so relevant pairs of the other variables calculated at North River are plotted in Figure 4. Note that the vertical lines in Figure 4(d) are due to the measurement of depth h occurring at the increment of the field meter, and do not indicate a physical relationship. The only distinct relations are seen in Figure 4(b) and Figure 4(c), where both ![]()
and ![]()
appear to have an inverse relationship to![]()
.
3.2. Observed Froude Number Relationships in Field Data
As the variable ![]()
appears to have the most correlation to other variables in Equations (25) and (26), it is compared to the ratio of inertial terms to gravity terms at North River, displaying a similar inverse relationship as seen in Figure 5(a). When the ratio of the inertial terms to gravity terms is greater than 0.5, there are very few values of ![]()
greater than 3000 meters-seconds−1. The same relationship is plotted for the Miami Canal data in Figure 5(b). As described above, the spatial acceleration term cannot be calculated at this site and only the temporal acceleration is considered. However, the relation-ship of ![]()
and the ratio of terms are similar, with an approximate maximum ![]()
value of 3000 meters-seconds−1 at a ratio of terms value 0.5. One alternative might be to replace ![]()
with 1/Fr2, a non-dimensional parameter, but doing this with the North River data produces a poorer relationship to the ratio of inertial terms to gravity terms, as seen in Figure 5(c).
The results in Figure 5 indicate that values of ![]()
greater than 3000 meters-seconds−1 strongly indicate than inertial terms are less than half of the gravity terms. However, values of ![]()
less than 3000 meters-seconds−1 seem to occur at both high and low inertial/gravity values. So this parameter can only confirm that inertial forces are not important.
3.3. Deriving the Hydrodynamic Significance Number
Equation (12) can be divided by Equation (22) in finite-difference form to get the ratio of the inertial to gravity terms:
![]()
(27)
Multiplying numerator and denominator by Δt and rearranging:
![]()
(28)
Defining ![]()
as the advective Courant Number:
![]()
(29)
where HSN is the Hydrodynamic Significance Number, which can be defined with six dimensionless numbers:
![]()
is the Froude Number squared;
![]()
is the temporal change in the Froude Number squared divided by the Froude Number squared;
![]()
is the spatial change in the Froude Number squared divided by the Froude Number squared;
![]()
is the temporal change in depth divided by the depth;
Cr is the advective Courant Number ![]()
and;
![]()
is the bed elevation spatial difference divided by the depth.
Equation (29) can be recalculated with the numerator only representing the temporal acceleration Term A in Equation (2) to yield a modified Hydrodynamic Significance Number:
![]()
(30)
Note the sign change in the numerator between Equations (29) and (30). This corresponds to the formulation in [6] which also has a sign difference in the Froude Number term between the temporal and spatial acceleration terms.
3.4. Hydrodynamic Significance Number in Field Data
Miami Canal has good hydrologic conditions for evaluating Equation (29), but lacks downstream discharge meas- urements that are needed to compute the spatial acceleration term. North River has both upstream and downstream measurements of discharge and depth, but large variations in channel width, 13 meters at the up-stream site and 80 meters at the downstream site. The unit width form of the continuity equation (Equation (8)) was used for deriving the Hydrodynamic Significance Number, which assumes a constant width over the distance Δx. This assumption applies to a uniform numerical grid, as in a numerical model, but is obviously contradicted in the case of North River field data.
Given these limitations in both North River and Miami Canal field data, the spatial acceleration terms are neglected for comparisons to these data. The modified HSNt in Equation (30) is compared to the temporal ace- leration (A in Equation (2)) divided by the gravity term (C in Equation (2)) for upstream North River and upstream Miami Canal. Six-hour average values are plotted in Figure 6; the temporal averaging helping to mitigate mea- surement and timing errors. Figure 6(a) shows very poor correlation for the North River station, with an R2 value of 0.003, but a good relationship is shown in Figure 6(b) for Miami Canal with an R2 value of 0.847. The most obvious explanation for this big difference between the two locations is that North River has quite a variable width whereas Miami Canal has a relatively constant width. This appears to be a factor even when not considering the spatial acceleration term. The other observation from Figure 6 is that HSNt values are consistently smaller than the ratio of terms for both sites. Neglecting the spatial acceleration terms may be a factor in this, but a more likely cause is the large Δx distances between upstream and downstream stations, which violates the small increment assumption for Δx, creating a larger value of Cr and a smaller HSNt. Despite these limitations, Figure 6(b) indi- cates that, for a system of relatively constant flow width, the Hydrodynamic Significance Number can be a rep- resentative indicator of the relative magnitude of the inertial forces relative to gravity forces.
4. Applying Hydrodynamic Significance Number in Numerical Models
Applying the Hydrodynamic Significance Number to numerical model simulations avoids the bias due to variable channel width, as the cell to cell widths are the same. This provides an indicator of when and where the flow conditions warrant a full hydrodynamic solution. In order to examine the importance of the inertial terms, several simulations were performed with the SWIFT2D hydrodynamic code and the SWR diffusion-analogy code.
4.1. Miami Canal Test Problem Description
A test problem was constructed using the SWIFT2D simulator and represented a 3.05 kilometer section of the Miami Canal upstream of hydraulic gate/structure S-26 (Figure 1 and Figure 7). In this area, the canal is oriented with flow originating from the northwest and flowing toward the southeast. The gate is operated in response to upstream and downstream stage levels. The input data was synthesized from a combination of flow and stage data measured 366 meters upstream of S-26 and stage data measured at S-26. The model simulates 335 days beginning on January 1, 2008 and ending December 1, 2008.
The model is composed of 128 columns and 7 rows of 25-meter-square grid cells. The upstream boundary is a time-varying stage boundary and a flow boundary, based on the measurement station, is established downstream
![]()
Figure 6. Comparison of the ratio of inertial/gravity terms to: (a) Modified Hydrodynamic Significance Number at North River and (b) Modified Hydrodynamic Significance Number at Miami Canal.
![]()
Figure 7. Model grid setup for Miami Canal simulation.
to simulate gate operations. The active model can be divided into two sections. A 122 column long by 1 row wide segment is located through the center of the model with the last cell containing the downstream flow boundary. In addition, a 4 column by 5 row pool is added to the upstream section in order to maintain more stable specified stage levels and provide adequate boundary inflows (Figure 7). All other boundaries were specified as no-flow.
Bottom elevations were fixed at −5.00 meters for the widened pool section and were set to −2.64 meters for the simulated canal section. The vertical datum used was the North American Vertical Datum of 1988 (NAVD88). For stability, a constant time step of 18 seconds was required. In order to isolate the hydrodynamic effects, precipita- tion, evapotranspiration and wind were not included in any of the simulations. All cells were given an equal Manning’s n value of 0.02, which is within the common range of 0.02 - 0.03 for straight, uniform dredged/ex- cavated channels [26] .
The stage boundary input data were linearly extrapolated to the boundary 3 kilometers upstream of the structure using stage data measured at S-26 and at the field station 366 meters upstream of S-26 (Figure 7). The flow vo- lumes used at the downstream boundary were set to measured values at the station 366 m upstream S-26. The data were measured and applied to the model in 15-minute increments throughout the simulation.
The Hydrodynamic Significance Number (HSN) was computed using the time series output from the Miami Canal numerical model and Equation (29). A 300-minute period of time was chosen which covers the gate opera- tions creating the highest peak in the friction term seen on June 20, 2008 (Figure 3). The time series of HSN at various distances upstream of the gate is shown with the simulated stage and flow at the gate in Figure 8. Time 0 minutes corresponds to 14:26 hours on June 20, 2008. At approximately time 66 minutes, the S-26 gate is opened and the discharge peaks as the stage drops. Higher HSN values result and a cyclic fluctuation is seen. The HSN exceeds a value of 1 at the earlier peaks after the gate opening, but at later times only exceeds a value of 1 at the location furthest upstream (2650 meters). The cyclic fluctuation appears to be an artifact of the boundaries, in that the travel time for a gravity wave in the 3-meter-deep canal traversing the 3050 meter length of the model area and back is about 19 minutes. This is approximately the length of the oscillatory cycle seen in Figure 8. This fluctuation is difficult to see in the stage or flow data, and reveals that boundary effects can be subtle in a hydrodynamic model.
![]()
Figure 8. Stage, Flow, and Hydrodynamic Significance Number generated by Miami Canal model.
Note that the HSN values in Figure 8 are much large than those in Figure 6 and are more of the size ex- pected to represent the ratio of inertial to gravity terms. The effects of using different schemes are examined next.
4.2. Synthetic Test Problem Description
A purely synthetic test problem was also created using the SWIFT2D simulator to examine the importance of inertial terms and the use of the Hydrodynamic Significance Number. Ten scenarios were simulated with different flow rates and frictional resistances. Each test case was initiated with a common initial stage and designed to drain and reach a static state of 1-meter-deep flow to the east down a sloped surface. Each simulation lasted 7 days and the transient period from each case was plotted and compared.
The model utilized 500-meter-square grid spacing and consisted of 10 active rows and columns resulting in 100 active cells (Figure 9). The western boundary was set up as a constant inflow boundary. The eastern boundary was simulated with a fixed stage of 1.05 meter, which maintained a 1 meter depth. The northern and southern boun- daries were simulated as no-flow boundaries. Bottom elevations decreased uniformly from west to east with a cell center value of 1.05 meter in the western most active cell and a cell center value of 0.05 meter in the eastern most active cell. All cases had an initial stage of 2.05 meter and a constant time step of 6 seconds. The simulation is begun with the defined flow rate on the west boundary held steady and the stage on the east boundary immediately dropped to 1.05 meters. The transient response depends on the flow and velocities, and the simulation approaches steady state.
![]()
Figure 9. Model grid for synthetic problem.
A variety of input flow rates and Manning’s n values were chosen to produce a steady-state flow condition with 1-meter-deep flow for all 10 cases. The Manning equation was used to specify the western boundary flow rates for each Manning’s value chosen and is defined as:
![]()
(31)
where V is the velocity, n is the Manning’s value, R is the hydraulic radius defined as the cross-sectional area of flow divided by the wetted perimeter, and S is the slope of the water surface. Equation (31) shows that velocity and Manning’s n are inversely proportional. With a 1 meter flow depth, a 0.0002 meter/meter slope, and a hydraulic radius of 1 meter, several test problems were constructed with various Manning’s n values and corresponding flow rates (Table 2). By varying the flow velocity and friction, and maintaining the same steady-state flow depth, the ratio of the inertial terms to the gravity term is varied and the effects on flow and Hydrodynamic Significance Number can be examined.
The Hydrodynamic Significance Number (HSN) was computed from the synthetic test problem output for differing values of Manning’s n. The values at selected columns (identified in Figure 9) are shown in Figure 10. The HSN values for the simulation with n = 0.03 are an order of magnitude larger than those with n = 0.3. The peak values are erratic and do not occur at the same location or time in the two simulations. As in the Miami Canal simulation shown in Figure 8, the pattern indicates wave oscillations are predominantly affecting the HSN. However in this case, the system settles to steady-state after only a couple of oscillations. The peak HSN for the case of n = 0.03 is 3.6, showing that the inertial terms are substantially higher than the gravity terms. When n = 0.3 the peak HSN is only 0.30.
The behavior of the system can be seen from the stage time series as shown in Figure 11. In the case where Manning’s n = 0.03, the simulation with inertial terms displayed a lag in the stage drop compared to the noniner- tial simulation. This difference is not seen to nearly the same degree in the case where Manning’s n = 0.3, as flow velocities and inertial effects are much smaller. This deviation in stage solution depending on the inertial terms is indicated by the higher HSN numbers in Figure 10.
The flow velocities at the center row for different columns are shown in Figure 12. The hydrodynamic solution tends to have lower velocities than the noninertial solution at the beginning and larger values than the noninertial solution at the end. This is consistent with the fact that the hydrodynamic solution takes momentum changes into account and represents changes in flow more sluggishly. As was the case in the previous figures, the difference between the hydrodynamic and noninertial solution is much less when Manning’s n is 0.3.
![]()
Table 2. Manning’s n values and corresponding velocity and flow for synthetic test case.
![]()
Figure 10. Hydrodynamic Significance Number at column locations in synthetic test problem.
5. Summary and Conclusions
A formulation was derived in terms of several dimensionless numbers that represents the ratio of the inertial terms to the gravity term in the conservation of momentum equation. Important parameters were identified by com-
![]()
Figure 11. Computed stage at column locations in synthetic test problem.
parisons with field data collected at two waterways in South Florida. The formulation was used to develop a Hydrodynamic Significance Number (HSN) that is combined with simulations of field site and synthetic scenarios to indicate flow situations where the inertial terms are important.
The parameter ![]()
was identified as a having a significant correlation to hydrodynamic dominance in the field data. At times when ![]()
is greater than about 3000 meters-seconds−1, inertial terms are consistently less than half of the gravity terms. Lower values of ![]()
encompass almost all of the higher inertial/gravity values, but also a number of lower values. So the parameter ![]()
can be a good indicator of when hydrodynamic forces do not dominate, but a less useful indicator of when they do.
The two field sites represent substantially different conditions, with the Miami Canal site more controlled than North River. The peak hydrodynamic effects are commonly associated with boundary transients such as when the hydraulic control structure on Miami Canal is opened or closed. North River has a large variation in cross section between the upstream and downstream stations, whereas Miami Canal is quite uniform. This difference is the most likely factor causing HSN to show good correlation to the ratio of the inertial and gravity terms at Miami Canal but a bad correlation at North River. A numerical model solution with constant-width grid cells would not have this problem.
The effect of the hydraulic control on the Miami Canal site, relative to North River, can be seen in the behavior of the inertial and other terms in the momentum equation. Whereas the North River data produce more gradually varying terms, the Miami Canal data yield sudden peaks in the inertial and friction terms. However, at more nat-
![]()
Figure 12. Computed velocity at column locations in synthetic test problem.
ural sites like North River the inertial terms can pre-dominate at times when the gravity term is low (near hori- zontal slope).
The synthetic test problem indicated that the inertial terms are more important at lower frictional resistances for similarly configured systems. The difference in results from a hydrodynamic solution and a diffusion-analogy solution depends on the magnitude of the HSN.
The formulations developed can be applied to both field measurements and numerical models to help evaluate when inertial terms are important. Both ![]()
and the HSN are relatable to the Froude Number and demonstrate the relationships of dimensionless numbers important to hydrodynamic dominance.
Notation
A cross-sectional area;
Cr advective Courant Number,![]()
;
Fr Froude Number,![]()
;
g gravitational acceleration;
h depth of water![]()
;
k Manningsn squared in SI units or Manningsn squared divided by 2.208 in English units;
Q discharge;
R hydraulic radius (area divided by wetted perimeter);
t time;
v flow velocity;
x distance;
Z stage;
Ε bottom bed elevation.