A Unified CFD Based Approach to a Variety of Condensation Processes in a Viscous Turbulent Wet Steam Flow ()
1. Introduction
The theory of non-equilibrium inviscid spontaneously condensing flow has been presented in a number of reviews and monographs and applied in stationary and nonstationary airfoil, nozzle and bladed passage calculations ( [1] [2] [3] [4] [5] ). Although pure condensation by homogeneous nucleation is not frequently found in nature, the concepts developed for homogeneous vapor phase nucleation form the foundation of analysis of heterogeneous condensation on extraneous pre-existing particles. Consistent methodology of solution of the related problems involves an explicit time-marching algorithm in Eulerian or Eulerian-La- grangian frame for solving the main flow conservation equations, linked with the classical theory of nucleation and droplet growth. Little information is available in the literature on the application of droplet formation in three-dimensional flows ( [5] - [11] ). Correct application of viscous physical models to the two-phase non equilibrium flow features the interaction of condensation with the secondary flow, boundary layers, shock, and wake gas-dynamic systems.
In the present paper, an accurate procedure, based on Navier-Stokes equations with turbulent effect, simulated according to the Baldwin-Lomax model [12] , is developed for the calculation of the condensation process in 2D flow passages.
The effect of turbulent pulsations on the kinetic equations is investigated. The problem of closing based on momentum kinetic equations (Hill’s chain, [13] ) is generalized for the case of turbulence and arbitrary expression of the droplet growth. There has been recent interest in modeling the process of condensation in the presence of electric field. To address this, changes in kinetic model are introduced and the model of closing is proposed.
The implicit second order accurate TVD type relaxation technique was mo- dified to solve the Navier-Stokes system of conservation laws for the medium and condensate mass fraction. High spatial resolution is achieved by implementing the two-phase discontinuity breakdown analytical solution into the numerical technique of flux computations. The procedure was found to provide stable convergence without any artificial dissipation.
2. Basic Model
In the absence of velocity slip the compressible Navier-Stokes conservative equations of mass, momentum and energy for the wet steam flow take an identical form to its single-phase counterpart ( [1] [6] )
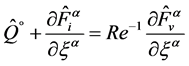 (1)
(1)
where
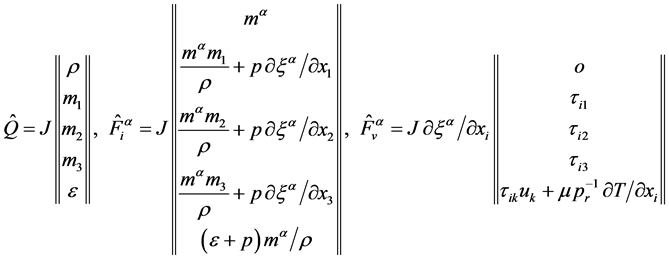
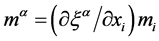 ,
, 
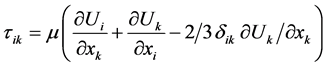
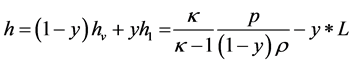
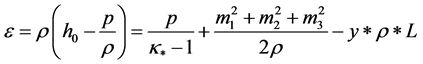
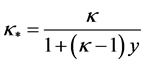
The usual convention is assumed everywhere when a letter appearing twice in one term is regarded as being summed from 1 to 3. The dotted terms indicate partial derivatives with respect to time. The system (Equation (1)) is not complete since the last additive term in the expression of enthalpy h, representing heat release to the flow, is proportional to the unknown condensate mass fraction, y. The latter can be deduced from the conservation law for the liquid formation, including nucleation and growth of the existing droplets and existing charge, bearing by droplets. Considering primary polydispersed condensate, it’s possible to treat droplets as a continuum by the use of a statistical function distribution as a function of time, space coordinates, droplet radius and droplet charge  such as
such as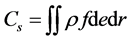 ―concentration of condensate,
―concentration of condensate, 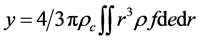 ―wetness,
―wetness,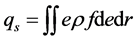 ―concentration of charge at the current moment of time at the current location.
―concentration of charge at the current moment of time at the current location.
The closure balance for corresponding function of drop size distribution may be derived from the condition of mass conservation (V―denotes Cartesian volume).
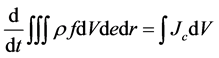 (2)
(2)
Using the divergence theorem, a multidimensional integral with variable limits can be expressed as a surface integral over the boundary “enclosing” the fluid boundary, droplet size and charge boundaries. Omitting some intermediate derivations, the final result, relating to the laminar flow, may be presented in the following form (subscript after comma means partial derivation by corresponding variable).
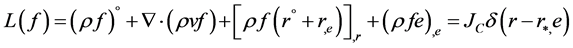 (3)
(3)
The expressions of the nuclei rate, 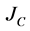 , critical droplet size r∗ and droplet size growth rate
, critical droplet size r∗ and droplet size growth rate , taking into account the charge, borne by the droplet, can be found in [14] .
, taking into account the charge, borne by the droplet, can be found in [14] .
Describing a turbulent flow of a condensate we assume traditional Boussinesq’s type relation, which constitutes the corresponding turbulent mass flow as proportional to the gradient of function distribution (the prime sign ( ) indicates turbulent pulsation, bar above―averaging)
) indicates turbulent pulsation, bar above―averaging)
 (4)
(4)
As a result of an averaging of convective terms in Equation (3) arrive to the closure balance to determine unknown function distribution ![]()
![]() (5)
(5)
Averaging terms, relating to nucleation rates, droplet size and charge growth needs special investigation and is omitted here. In all calculations these terms have been considered in quasi-laminar approximation.
The value of droplet charge growth, incorporated into kinetic Equation (5), is governed by elementary charge precipitation. The charge on a particle can result from two sources: field charging and diffusion charging. If a particle is in a uniform electric field, ions will travel along the electric field lines and deposit on the particle ( [14] [15] ). Ultimately a charge is accumulated sufficient to repel additional ions and the saturation charge is attained. Diffusion charging occurs as a result of collisions between ions and particles due to the random thermal motion of the ions. Diffusion charging is a much slower process than field charging but becomes the dominant mechanism for sub-micron particles. Generally the charging mechanism can be represented in the following unsteady form convenient to implement in the original time marching frame![]() . The complete set of details relating to the charging phenomena may be found in [14] [15] .
. The complete set of details relating to the charging phenomena may be found in [14] [15] .
The final closure to determine the evolution of charge bearing by droplets can be modeled by equations of electrodynamic field, where the contribution of moving charges on electric field is taken into account (q―space density of electrical field, b, D―field and diffusion coefficients)
![]() (6)
(6)
Equations ((5) and (6)) describe the procedure of charging disperse phase, which becomes the ions carrier, in the neighborhood of corona discharge. Distribution of charge in an electric field at initial moment of time based on a statistical evaluation of experimental measurements, serves as an initial condition for the time dependent electromagnetic problem. Equations of hydrodynamics (1) and kinetic Equation (3) must be solved simultaneously with the Maxwell Equation (6), and thermodynamic relations.
2.1. Equilibrium Condensation
Wet steam calculations simulate the flow under the vapor dome where both liquid and vapor phases exist in thermodynamic equilibrium. The equilibrium pressure of a vapor coexisting with its liquid or solid phase is given by the Clausius-Clapeyron type relations![]() . With this dependence the kinetic Equation (5) are taken out of consideration, simplifying as a result the computational problem. The flow domain consists of two types of regions: the first one without condensation (supersaturation S < 1) which is identical to the classical single phase analysis. The second region is described by Equation (1) with the pressure value determined by equilibrium condition. Reference [16] contains the details of implementation of an equilibrium condensation model into our computer code analysis of a wet steam flow in a multistage turbine.
. With this dependence the kinetic Equation (5) are taken out of consideration, simplifying as a result the computational problem. The flow domain consists of two types of regions: the first one without condensation (supersaturation S < 1) which is identical to the classical single phase analysis. The second region is described by Equation (1) with the pressure value determined by equilibrium condition. Reference [16] contains the details of implementation of an equilibrium condensation model into our computer code analysis of a wet steam flow in a multistage turbine.
2.2. Homogeneous Non-Equilibrium Condensation
To reduce the computation time we replace Equation (5) by a set of momentum equations. For simplicity we omit electrical terms. Multiplying (5) by rk (k = 0, 1, 2, 3) and integrating from r = r∗ to r =∞, we explore the usual way to reduce the problem to the more compact space of variables
![]() (7)
(7)
If droplet growth does not depend on r, the known momentum equations are derived. Usually for droplets r > 1 μm the Knudsen’s expression for ![]() independent on r is no longer valid. To extend validity of the momentum approach to the bigger droplet size we approximate r by the linear form,
independent on r is no longer valid. To extend validity of the momentum approach to the bigger droplet size we approximate r by the linear form, ![]() , converting the integral―differential Equation (7) to the following system of partial differential equations
, converting the integral―differential Equation (7) to the following system of partial differential equations
![]() (8)
(8)
3. Numerical Technique
The linked system of partial derivative equations is solved on an adaptive curvilinear mesh. Using limited extrapolations of the conservative variables, the fluxes are evaluation according to the TVD approach described, for instance, in [17] [18] [19] . The general Riemann problem for discontinuity breakdown in a two phase mixed flow is utilized to evaluate the inviscid fluxes at the edges of each cell. The convective part of implicit operator is built by using the upstream differences with consideration of the sign of the characteristic speed (eigenvalues of the Jacobean matrix). Implicit boundary conditions for the variations of variables are incorporated. The basic solver strategy employs a Gauss-Seidel relaxation procedure, sequentially applied to the systems of Equations [1] and [8] . In addition Newton sub-iterations are used at each global time step to increase stability and reduce linearization errors. The procedure is of the second order accurate in both space and time and provides stable convergence without any artificial dissipation. Further details of numerical technique can be found in [17] [18] [19] [20] .
4. Results
Calculations have been applied for the two-dimensional viscous superheated and super cooled, spontaneously condensing flow through the rotor cascade described in [21] [22] . The experiment performed at a downstream isentropic Mach number Ma = 1.2 and a Reynolds number of about 500,000 based on a cascade chord. The following parameters of the flow were imposed: flow inlet angle between the stream and circumferential direction of 128˚, stagnation pressure at the inlet section Pο = 1.008 bar; stagnation temperature Tο = Ts(Pο) − 5.7 K (for super cooled steam), Pο/Pout =2.32. Calculations were done on 100 × 60 grid, with 61 nodes normal to the surface and the first point away from the surface y+ < 2. Figure 1 shows the calculated domain and the grid over the cascade. Figure 2 shows the calculated wall pressure for this case. The calculated data are compared with experimental data, measured along pressure and suction sides, where the pressure distributions are observed of being typical of this type of airfoil and Mach number. Local deceleration at the leading edge is associated with corresponding over-expansion at the suction side. A slight inflection (plateau) in the pressure distribution can be seen from both experimental and theoretical distributions, affected by an abrupt change of surface curvature at approximately 40% of axial chord. Figures 3-7 show the data from the case characterized by the initially super-cooled steam, in which spontaneously condensation is known to occur within the cascade passage. The same blade geometry and analysis grid is used. Figure 3 contains the airfoil pressure distributions on the pressure and suction sides, plotted alongside the measured wall pressure data. The pressure rise on the suction side is associated with over-expansion at the leading edge and a rapid condensation at approximately 50% of axial chord. The first pressure rise is located at the same position as its counterpart from the superheated test. The second rise of pressure is caused by the heat release during
![]()
Figure 1. “H” type grid 120 × 60 for 2D cascade viscous simulation.
![]()
Figure 2. Wall pressure distribution for superheated test.
![]()
Figure 3. Surface pressure distribution. Nucleating test.
rapid condensation (heat shock) and corresponds to the location with the abrupt change of curvature on a suction side. Figure 4 shows static pressure contour lines inside the flow passage and indicates both types of discontinuities: heat shock, pertaining to the heat reveal and Rankin-Hugoniot shock, associated with the trailing edge. Figure 5, Figure 6 show wet condensate fraction contours in the flow-field passage. The combined effect of viscous turbulent boundary layer is quantified. As the temperature in the boundary layer rises approaching the wall, the super-cooling decreases and the droplet growth and heat release to the
![]()
Figure 4. Static pressure contours. Nucleating test.
![]()
Figure 6. Wetness fraction contours at the trailing edge.
![]()
Figure 7. Distribution of averaged droplet radius across flow passage.
flow weakens and vanishes to zero at the solid walls. Comparing condensate wetness fraction with its counterpart obtained by inviscid simulation reveals the absence of liquid fraction very near the wall in the viscous simulation. The phenomenon was discovered originally in [22] using visualization by light scattering of transonic condensing internal flow, that showed the existence of a near wall zone without droplets. Similar results for a nozzle and a cascade were numerically obtained in laminar approximation in [9] . Variation of droplet radius along circumferential mesh line at four axial coordinate locations x = 0.6, 0.9, 1, 1.5 (non-dimensional, referenced to the axial chord) are shown in Figure 7. The distribution of droplet size is quite consistent―dramatically decreasing in the boundary layers at the suction and pressure sides by the reason discussed above, and generally diminishing from suction side to the pressure side within the core of the flow. At the trailing edge, the calculations indicate low concentration (20 times lower than in the core flow) of relatively big droplets―0.9 micron. Downstream the radius of droplets is approximately 0.05 micron with a slight variation across the pitch. Results may be compared with the 0.025 - 0.05 micron size range deduced from the light extinction measurements at this position [22] .
5. Conclusions
A family of quasi linear mathematical models is presented and calculations made for viscous turbulent wet steam flow with a variety of condensation phenomena. These models can be applied to the analysis of equilibrium condensation, homogeneous (spontaneous) condensation, heterogeneous condensation on extraneous particles, and condensation of charged dispersed phase moving in an electrostatic field. The unified model is represented by coupled systems of gas dynamic equations for viscous turbulent two-phase flow, kinetic and electro- kinetic equations tracing out combined processes of size and charge growth and electromagnetic field equations described an electric field with an account of self-induced in-part by a moving electrical cluster.
The effect of turbulent pulsations on the kinetic equations is investigated. The problem of closing based on momentum kinetic equations (Hill’s chain, [12] ) is generalized for the case of turbulence and arbitrary expression of the droplet growth. There has been recent interest in modeling the process of condensation in the presence of electric field. To address this, changes in kinetic model are introduced and the model of closing is proposed.
The implicit second order accurate TVD type relaxation technique was implemented to solve the Navier-Stokes system of conservation laws, supplemented by the Baldwin-Lomax turbulence model for the medium and condensate mass fraction. The numerical procedure is time marching, monotone, implicit, of second order accuracy by space and time coordinates, and exhibits high resolution shock capturing ability. Viscous flow field calculations made with this procedure reveal significant influence on condensation by the shear boundary layers and wakes. Distributions of cooling rate, droplet radius and parameters of the bulk flow are predicted. Verification of the codes against known experimental data is presented. The procedure was found to provide stable convergence without any artificial dissipation.
Acknowledgements
The authors gratefully acknowledge support of this work by the Electric Power Research Institute. They are grateful to Professor F. Bakhtar for the valuable information supplied relating to the experimental data.
Nomenclature
![]() = intensity of electrostatic field
= intensity of electrostatic field
e = charge bearing by the droplet
![]() = contravariant vector of conservation variables
= contravariant vector of conservation variables
![]() = contravariant components of inviscid fluxes
= contravariant components of inviscid fluxes
![]() = contravariant components of viscous fluxes
= contravariant components of viscous fluxes
f = statistical function distribution of the number of particles
h = internal enthalpy of the mixture per unit mass
J = Jacobian of coordinates transformation
Jc = nucleation rate per unit volume
L = latent heat of the phase transition
mi = Cartesian components of momentum
mα = contravariant components of momentum
p = static pressure of the mixture
Pr = Prandtl number
Re = Reynolds number
![]() = turbulent Reynolds number
= turbulent Reynolds number
r = radius of droplets
r∗ = Kelvin-Helmholtz critical radius
![]() = turbulent Schmidt number
= turbulent Schmidt number
T = static temperature of the vapor
![]() = Cartesian components of velocity
= Cartesian components of velocity
![]() = Cartesian coordinates
= Cartesian coordinates
y = wetness fraction
δ = delta function
δik = Kronecker delta
ε = total internal energy of the mixture per unit volume
κ = specific heat ratio
![]() = dynamic viscosity
= dynamic viscosity
τik = Cartesian components of stress tensor
ξα = curvilinear coordinates
![]() = gradient operator
= gradient operator