Chaos in a Fractional-Order Single-Machine Infinite-Bus Power System and Its Adaptive Backstepping Control ()
1. Introduction
As a mathematical branch with a history of over 300 years, fractional calculus and its applications to physics and engineering have attracted increasing attentions in recent years [1] [2] . Fractional calculus provides a good instrument to describe the memory, hereditary, non-locality and self-similarity properties of various materials and processes. Many chaotic systems, such as Lorenz system [3] , Chua’s system [4] , Duffing system [5] , Rössler system [6] , Chen system [7] and so on, still remain chaotic when their equations become fractional.
Chaotic phenomena have been observed in power systems during the past few decades [8] - [13] . Chaos causes electromechanical oscillations to behave randomly, which are harmful to the secure and stable operation of power systems, and even produce undesired negative consequences, such as angle divergence, voltage collapse and system splitting [14] . So far, almost all the studies of dynamics of power systems are concerned with the integer-order models, and there are little research results on fractional modeling and control design of power systems. Tan et al. studied the dynamics of a fractional-order interconnected power system and found that the system became chaotic when the fractional order is no less than 0.88 [15] . Sun and Li investigated the chaotic and bifurcation phenomena in a fractional-order three-bus power system and the existence of chaos was demonstrated for different orders [16] .
In this paper, we numerically investigate the chaotic dynamics of a fractional-order single-machine infinite-bus (FOSMIB) power system. Period-doubling bifurcation and chaos are observed in FOSMIB power system and the existence of chaos is confirmed by evaluating the largest Lyapunov exponent (LLE). Based on the fractional-order backstepping method, an adaptive controller is presented to suppress chaos in the FOSMIB power system, and the effectiveness of the proposed controller is proved by the numerical simulation results.
The rest of the paper is organized as follows. Some definitions and lemmas about fractional calculus are introduced in Section 2. The dynamics of the FOSMIB power system are analyzed in Section 3. An adaptive controller is designed using the fractional-order backstepping method to suppress chaos in the FOSMIB power system in Section 4. Finally, conclusions are addressed in Section 5.
2. Preliminaries
There are several different definitions of fractional derivatives. The most appropriate one for practical problems is the Caputo definition. The Caputo fractional derivative is given by
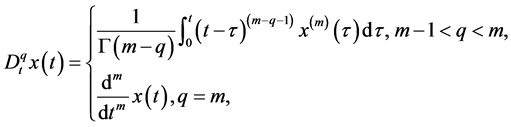 (1)
(1)
where m is integer and 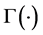 is the Gamma function.
is the Gamma function.
The Caputo fractional derivative satisfies the following properties:
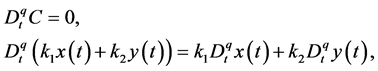 (2)
(2)
where C, 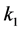 and
and 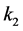 are real constants.
are real constants.
Lemma 1. [17] - [19] Consider the fractional-order system
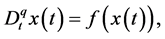 (3)
(3)
where 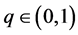 and
and . The equilibrium point
. The equilibrium point  of system (3) is locally asymptotically stable if all the eigenvalues
of system (3) is locally asymptotically stable if all the eigenvalues 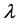 of the Jacobian matrix
of the Jacobian matrix  satisfy
satisfy
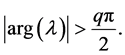 (4)
(4)
Lemma 2. [20] Let  be a continuous differentiable function. Then, at any instant the following inequality holds
be a continuous differentiable function. Then, at any instant the following inequality holds
 (5)
(5)
A continuous function 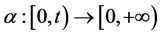 is referred as class-K if it is strictly increasing and
is referred as class-K if it is strictly increasing and  [21] .
[21] .
Lemma 3. (Fractional-order extension of Lyapunov direct method [22] ) Let  be an equilibrium point of the nonautonomous fractional-order system
be an equilibrium point of the nonautonomous fractional-order system
 (6)
(6)
with initial condition![]() . Assume that
. Assume that ![]() is a Lyapunov candidate and
is a Lyapunov candidate and ![]() are class-K functions. Then
are class-K functions. Then ![]() is asymptotically stable if the following conditions hold
is asymptotically stable if the following conditions hold
![]() (7)
(7)
![]() (8)
(8)
where ![]() and
and ![]() denotes an arbitrary norm.
denotes an arbitrary norm.
3. The FOSMIB Power System
In [12] Chen et al. analyzed the angle dynamics of the classical single-machine infinite-bus (SMIB) power system, which is governed by the so-called swing equation
![]() (9)
(9)
where M is the moment of inertia, D is the damping constant, ![]() is the maximum power of generator and
is the maximum power of generator and ![]() is the power of the machine.
is the power of the machine.
Let ![]() and
and![]() , then Equation (9) can be rewritten as
, then Equation (9) can be rewritten as
![]() (10)
(10)
where![]() ,
, ![]() and
and ![]() are positive constant parameters. When
are positive constant parameters. When![]() ,
, ![]() ,
, ![]() and
and![]() , the SMIB power system is chaotic.
, the SMIB power system is chaotic.
Here, we consider the fractional-order single-machine infinite-bus (FOSMIB) power system
![]() (11)
(11)
where ![]() is the fractional order. When
is the fractional order. When![]() , system (11) is the original integer-order SMIB power system.
, system (11) is the original integer-order SMIB power system.
The autonomous system (11) (as![]() ) has two equilibrium points:
) has two equilibrium points: ![]() and
and![]() . For the equilibrium point O, the Jacobian matrix is
. For the equilibrium point O, the Jacobian matrix is
![]() (12)
(12)
and its eigenvalues are
![]() (13)
(13)
In both cases,![]() . According to Lemma 1, O is asymptotically stable.
. According to Lemma 1, O is asymptotically stable.
For the equilibrium point E, the Jacobian matrix is
![]() (14)
(14)
and its eigenvalues are
![]() (15)
(15)
It can be seen that ![]() and
and![]() . In accordance with Lemma 1, E is unstable.
. In accordance with Lemma 1, E is unstable.
4. Dynamic Analysis of the FOSMIB Power System
In this section, we use the Adams-Bashforth-Moulton predictor-corrector algorithm proposed by Diethelm et al. in [22] - [24] to solve the FOSMIB power system (11). The dynamics are numerically analyzed by means of bifurcation diagrams, phase portraits and Lyapunov exponents. In the following simulations, parameter f is chosen as bifurcation parameter and the other parameters are fixed at![]() ,
, ![]() ,
,![]() . The initial conditions are selected as
. The initial conditions are selected as![]() ,
,![]() .
.
First, let![]() , and vary f from 2.4 to 3.5. The corresponding bifurcation diagram is plotted in Figure 1(a), from which a period-doubling route to chaos can be found. To confirm chaos, the largest Lyapunov exponent (LLE) is calculated using Wolf
, and vary f from 2.4 to 3.5. The corresponding bifurcation diagram is plotted in Figure 1(a), from which a period-doubling route to chaos can be found. To confirm chaos, the largest Lyapunov exponent (LLE) is calculated using Wolf
![]() (a) (b)
(a) (b)
Figure 1. Bifurcation diagram and the LLE versus f for q = 0.95: (a) Bifurcation diagram; (b) The LLE.
algorithm [25] and plotted in Figure 1(b). The FOSMIB power system is chaotic over most of the range![]() , where the LLEs are positive. The phase portraits for different values of f are plotted in Figure 2. With the increase of f from 2.4, period-1, period-2 and period-4 orbits are obtained at
, where the LLEs are positive. The phase portraits for different values of f are plotted in Figure 2. With the increase of f from 2.4, period-1, period-2 and period-4 orbits are obtained at![]() ,
, ![]() and
and![]() , respectively. After a cascade of period-doubling bifurcations, the system loses its stability and enters chaos at
, respectively. After a cascade of period-doubling bifurcations, the system loses its stability and enters chaos at![]() . As f increases further, the system becomes stable again via inverse period-doubling bifurcations.
. As f increases further, the system becomes stable again via inverse period-doubling bifurcations.
Now, let![]() ,
, ![]() ,
, ![]() ,
, ![]() and vary q from 0.87 to 1. The resulting bifurcation diagram is plotted in Figure 3(a), which indicates period-doubling bifurcations and chaos. The fractional-order SMIB power system is chaotic over most of the range
and vary q from 0.87 to 1. The resulting bifurcation diagram is plotted in Figure 3(a), which indicates period-doubling bifurcations and chaos. The fractional-order SMIB power system is chaotic over most of the range![]() , where the LLEs are positive as shown in Figure 3(b). The phase portraits for different values of q are plotted in Figure 4. With the increase of q from 0.87, period-1, period-2 and period-4 orbits are obtained at
, where the LLEs are positive as shown in Figure 3(b). The phase portraits for different values of q are plotted in Figure 4. With the increase of q from 0.87, period-1, period-2 and period-4 orbits are obtained at![]() ,
, ![]() and
and![]() , respectively. As q increases further, after a cascade of period-doubling bifurcations, a chaotic attractor is obtained at
, respectively. As q increases further, after a cascade of period-doubling bifurcations, a chaotic attractor is obtained at![]() .
.
5. Adaptive Backstepping Control of Chaos
In this section, an active controller is designed using fractional-order backstepping method to suppress chaos in the FOSMIB power system and stabilize it to the unstable equilibrium point![]() .
.
5.1. Controller Design
Consider the controlled FOSMIB power system
![]() (16)
(16)
![]()
Figure 2. Phase portraits for different values of f: (a) f = 2.5; (b) f = 2.55; (c) f = 2.61; (d) f = 2.65.
![]() (a) (b)
(a) (b)
Figure 3. Bifurcation diagram and the LLE versus q for f = 2.8: (a) Bifurcation diagram; (b) The LLE.
![]()
Figure 4. Phase portraits for different values of q: (a) q = 0.88; (b) q = 0.893; (c) q = 0.913; (d) q = 0.92.
where ![]() and the parameter f is unknown. The backstepping design procedure consists of two steps.
and the parameter f is unknown. The backstepping design procedure consists of two steps.
Step 1. Define![]() . Its derivative is given by
. Its derivative is given by
![]() (17)
(17)
where![]() ,
, ![]() is the virtual control to be defined later.
is the virtual control to be defined later.
Select the candidate Lyapunov function as
![]() (18)
(18)
Now, applying Lemma 2, it can be found that
![]() (19)
(19)
Define the virtual control ![]() as
as
![]() (20)
(20)
where ![]() is a positive constant, which leads to
is a positive constant, which leads to![]() . Substituting Equation (20) into Equation (17) and inequality (19), we have
. Substituting Equation (20) into Equation (17) and inequality (19), we have
![]() (21)
(21)
![]() (22)
(22)
Step 2. The derivative of ![]() is expressed as
is expressed as
![]() (23)
(23)
where ![]() is the estimate of
is the estimate of![]() . Choose the candidate Lyapunov function as
. Choose the candidate Lyapunov function as
![]() (24)
(24)
where k is a positive constant, which can adjust the speed of the adaptive law. Using Lemma 2, it can be found that
![]() (25)
(25)
Choose the control input and the adaptive law as
![]() (26)
(26)
![]() (27)
(27)
where ![]() is a positive constant. Substituting Equation (26) and Equation (27) into Equation (23) and inequality (25), we have
is a positive constant. Substituting Equation (26) and Equation (27) into Equation (23) and inequality (25), we have
![]() (28)
(28)
![]() (29)
(29)
According to Lemma 3, the closed-loop error system is asymptotically stable at the origin![]() . It means that, with the proposed controller and adaptive law, the FOSMIB power system is asymptotically stable at the equilibrium point
. It means that, with the proposed controller and adaptive law, the FOSMIB power system is asymptotically stable at the equilibrium point![]() .
.
5.2. Simulation Results
In the simulation, the fractional order q is equal to 0.95. The parameters of system (16) are taken as![]() ,
, ![]() ,
, ![]() and
and![]() . The parameters of the controller (26) and the adaptive law (27) are chosen as
. The parameters of the controller (26) and the adaptive law (27) are chosen as ![]() and
and![]() . The initial conditions are taken as
. The initial conditions are taken as![]() ,
,![]() . The initial parameter estimate is given by
. The initial parameter estimate is given by![]() . The closed-loop system consisted of Equations ((16), (26) and (27)) is solved by using the predictor-corrector algorithm. The simulation results are shown in Figure 5.
. The closed-loop system consisted of Equations ((16), (26) and (27)) is solved by using the predictor-corrector algorithm. The simulation results are shown in Figure 5.
The time-domain waveforms the states of the controlled system (16) are shown in Figure 5(a) and Figure 5(b). The FOSMIB power system has experienced chaotic behavior before the controller is put into effect. By activating the controller u at![]() , the chaotic behavior is suppressed and the controlled system converges to the equilibrium point
, the chaotic behavior is suppressed and the controlled system converges to the equilibrium point ![]() quickly. The parameter estimate
quickly. The parameter estimate ![]() is converged to
is converged to ![]() as shown in Figure 5(c) and the controller u is bounded as shown in Figure 5(d). From Figure 5, it can be seen that the proposed controller is feasible for suppressing chaos in the FOSMIB power system.
as shown in Figure 5(c) and the controller u is bounded as shown in Figure 5(d). From Figure 5, it can be seen that the proposed controller is feasible for suppressing chaos in the FOSMIB power system.
6. Conclusion
In this paper, we have numerically investigated the FOSMIB power system. The parameter f and the fractional order q are selected as bifurcation parameters respectively. Complex dynamical behaviors, such as periodic orbits, period-doubling bifurcations and chaotic attractors, are observed in the FOSMIB power system. The LLE is calculated using Wolf algorithm to confirm the existence of chaos. Furthermore, by exploiting the fractional-order backstepping method, we propose an adaptive controller to suppress chaos in the FOSMIB power system. The effectiveness of the presented controller is verified by numerical simulation results.
![]()
Figure 5. The time-domain waveforms of the controlled system (16).
Acknowledgements
The work was supported by the Natural Science Foundation of Henan Province, China (Grant No. 14A120005) and Excellent Young Scientist Development Foundation of Zhengzhou University, China (Grant No. 1421319086).