The exp(-φ(ξ))-Expansion Method and Its Application for Solving Nonlinear Evolution Equations ()
1. Introduction
The nonlinear partial differential equations of mathematical physics are major subjects in physical science [1] . Exact solutions for these equations play an important role in many phenomena in physics such as uid mechanics, hydrodynamics, optics, plasma physics and so on. Recently many new approaches for finding these solutions have been proposed, for example, extended Jacobian Elliptic Function Expansion Method [2] , the modified simple equation method [3] , the tanh method [4] , extended tended tanh-method [5] - [7] , sine-cosine method [8] - [10] , homogeneous balance method [11] [12] , F-expansion method [13] - [15] , exp-function method [16] [17] ,
trigonometric function series method [18] ,  -expansion method [19] - [22] , Jacobi elliptic function method [23] - [26] , the exp
-expansion method [19] - [22] , Jacobi elliptic function method [23] - [26] , the exp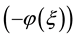 -expansion method [27] - [29] and so on.
-expansion method [27] - [29] and so on.
The objective of this article is to apply the exp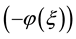 -expansion method for finding the exact traveling
-expansion method for finding the exact traveling
wave solution of dynamical system in a new double-Chain model of DNA and a diffusive predator-prey system which play an important role in biology and mathematical physics.
The rest of this paper is organized as follows: In Section 2, we give the description of the exp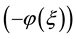 -ex-
-ex-
pansion method. In Section 3, we use this method to find the exact solutions of the nonlinear evolution equations pointed out above. In Section 4, conclusions are given.
2. Description of Method
Consider the following nonlinear evolution equation
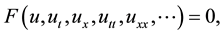 (2.1)
(2.1)
where 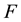 is a polynomial in
is a polynomial in 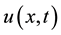 and its partial derivatives in which the highest order derivatives and nonlinear terms are involved. In the following,we give the main steps of this method:
and its partial derivatives in which the highest order derivatives and nonlinear terms are involved. In the following,we give the main steps of this method:
Step 1. We use the wave transformation
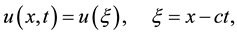 (2.2)
(2.2)
where 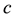 is a positive constant, to reduce Equation (2.1) to the following ODE:
is a positive constant, to reduce Equation (2.1) to the following ODE:
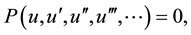 (2.3)
(2.3)
where 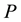 is a polynomial in
is a polynomial in 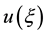 and its total derivatives,while
and its total derivatives,while 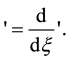
Step 2. Suppose that the solution of ODE (2.3) can be expressed by a polynomial in ![]() as follows
as follows
![]() (2.4)
(2.4)
where ![]() satisfies the ODE in the form
satisfies the ODE in the form
![]() (2.5)
(2.5)
the solutions of ODE (2.5) are when![]() ,
, ![]()
![]() (2.6)
(2.6)
when ![]()
![]() (2.7)
(2.7)
when ![]()
![]() (2.8)
(2.8)
when ![]()
![]() (2.9)
(2.9)
when ![]()
![]() (2.10)
(2.10)
where ![]() are constants to be determined later,
are constants to be determined later,
Step 3. Substitute Equation (2.4) along Equation (2.5) into Equation (2.3) and collecting all the terms of the same power![]() ,
, ![]() and equating them to zero, we obtain a system of algebraic equa-
and equating them to zero, we obtain a system of algebraic equa-
tions, which can be solved by Maple or Mathematica to get the values of![]() .
.
Step 4. substituting these values and the solutions of Equation (2.5) into Equation (2.3) we obtain the exact solutions of Equation (2.3).
3. Application
3.1. Example 1: Dynamical System in a New Double-Chain Model of DNA
An attractive nonlinear model for the nonlinear science in the deoxyribonucleic acid (DNA). The dynamics of DNA molecules is one of the most fascinating problems of modern biophysics because it is at the basis of life. The DNA structure has been studied during last decades. The investigation of DNA dynamics has successfully predicted the appearance of important nonlinear structures. It has been shown that the nonlinearity is responsible for forming localized waves. These localized waves are interesting because they have the capability to transport energy without dissipation [30] - [38] . In Ref. [37] [38] , it is given that a new double-chain model of DNA consists of two long elastic homogeneous strands which represent two polynucleotide chains of the DNA mole- cule, connected with each other by an elastic membrane representing the hydrogen bonds between the base pair of the two chains. Under some appropriate approximation, the new double-chain model of DNA can be des- cribed by the following two general nonlinear dynamical system:
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
where
![]() (3.3)
(3.3)
where![]() ,
, ![]() ,
, ![]() and
and ![]() denote respectively the mass density, the area of transverse cross-section, the Young’s modulus and tension density of each strand;
denote respectively the mass density, the area of transverse cross-section, the Young’s modulus and tension density of each strand; ![]() is the rigidity of the elastic membrance;
is the rigidity of the elastic membrance; ![]() is the distance between the two strands, and
is the distance between the two strands, and ![]() is the height of the membrance in the equilibrium positive. In Equations (3.1) and (3.2),
is the height of the membrance in the equilibrium positive. In Equations (3.1) and (3.2), ![]() is the difference of the longitudianl displacements of the bottom and top strands, while
is the difference of the longitudianl displacements of the bottom and top strands, while ![]() is the difference of the transverse displacements of the bottom and top strands.
is the difference of the transverse displacements of the bottom and top strands.
we first introduce the transformation
![]() (3.4)
(3.4)
where ![]() and
and ![]() are constants, to reduce Equations (3.1) and (3.2) to the following system of equations:
are constants, to reduce Equations (3.1) and (3.2) to the following system of equations:
![]() (3.5)
(3.5)
and
![]() (3.6)
(3.6)
Comparing Equations (3.5) and (3.6) and using (3.4) we deduce that ![]() and
and![]() . Now Equations (3.5) and (3.6) can be written as
. Now Equations (3.5) and (3.6) can be written as
![]() (3.7)
(3.7)
where
![]() (3.8)
(3.8)
The wave transformation![]() ,
, ![]() , reduce Equation (3.7) to the following ODE:
, reduce Equation (3.7) to the following ODE:
![]() (3.9)
(3.9)
where![]() . Balancing
. Balancing ![]() and
and ![]() yields,
yields,![]() . Consequently, we have the formal solution:
. Consequently, we have the formal solution:
![]() (3.10)
(3.10)
where ![]() and
and ![]() are constants to be determined, such that
are constants to be determined, such that![]() . It is easy to see that
. It is easy to see that
![]() (3.11)
(3.11)
substituting Equation (3.10) and its derivatives in Equation (3.9) and equating the coefficient of different power’s of ![]() to zero, we get
to zero, we get
![]() (3.12)
(3.12)
![]() (3.13)
(3.13)
![]() (3.14)
(3.14)
![]() (3.15)
(3.15)
Equations (3.12)-(3.15) yields
![]()
![]()
![]()
Thus the solution is
![]() (3.16)
(3.16)
Let us now discuse the following case:
Case 1. if ![]()
![]() (3.17)
(3.17)
Case 2. if ![]()
![]() (3.18)
(3.18)
Case 3. if ![]()
![]() (3.19)
(3.19)
Case 4. if ![]()
![]() (3.20)
(3.20)
Case 5. if ![]()
![]() (3.21)
(3.21)
3.2. Example 2. A Diffusive Predator-Prey System
Consider a system of two coupled nonlinear partial differential equations describing the spatio-temporal dyna- mics of a predator-prey system [39] ,
![]() (3.22)
(3.22)
where![]() ,
, ![]() ,
, ![]() and
and ![]() are positive parameters. The solutions of predator-prey system have been studied in various aspects [39] - [41] . The dynamics of the diffusive predator-prey system have assumed the following
are positive parameters. The solutions of predator-prey system have been studied in various aspects [39] - [41] . The dynamics of the diffusive predator-prey system have assumed the following
relations between the parameters, namely ![]() and
and![]() . Under there assumptions, Equation (3.22) can be rewritten in the form:
. Under there assumptions, Equation (3.22) can be rewritten in the form:
![]() (3.23)
(3.23)
We use the wave transformation ![]() to reduce Equation (3.23) to the following nonli- near system of ordinary differential equations:
to reduce Equation (3.23) to the following nonli- near system of ordinary differential equations:
![]() (3.24)
(3.24)
where ![]() is a nonzero constant.
is a nonzero constant.
In order to solve Equation (3.24), let us consider the following transformation
![]() (3.25)
(3.25)
Substituting the transformation (3.25) into Equation (3.24), we get
![]() (3.26)
(3.26)
Balancing ![]() with
with ![]() in Equation (3.26) yields,
in Equation (3.26) yields,![]() . Consequently, we get the same formal solution (3.10). Substituting Equation (3.10) and its derivatives in Equation (3.26) and equating the coefficient of different power's of
. Consequently, we get the same formal solution (3.10). Substituting Equation (3.10) and its derivatives in Equation (3.26) and equating the coefficient of different power's of ![]() to zero, we get
to zero, we get
![]() (3.27)
(3.27)
![]() (3.28)
(3.28)
![]() (3.29)
(3.29)
![]() (3.30)
(3.30)
Equations (3.27)-(3.30) yields
Case 1.
![]()
![]()
Case 2.
![]()
![]()
Thus the solution is
Case 1.
![]() (3.31)
(3.31)
Case 2.
![]() (3.32)
(3.32)
Let us now discuss the following cases:
Case 1.
Case (1.1). if ![]()
![]() (3.33)
(3.33)
Case (1.2). if ![]()
![]() (3.34)
(3.34)
Case (1.3). if ![]()
![]() (3.35)
(3.35)
Case (1.4). if ![]()
![]() (3.36)
(3.36)
Case (1.5). if ![]()
![]() (3.37)
(3.37)
Case 2.
Case (2.1). if ![]()
![]() (3.38)
(3.38)
Case (2.2). if ![]()
![]() (3.39)
(3.39)
Case (2.3). if ![]()
![]() (3.40)
(3.40)
Case (2.4). if ![]()
![]() (3.41)
(3.41)
Case (2.5). if ![]()
![]() (3.42)
(3.42)
4. Conclusion
We establish exact solutions for the dynamics of DNA molecules is one of the most fascinating problems of modern biophysics because it is at the basis of life. The DNA structure has been studied during last decades. The investigation of DNA dynamics has successfully predicted the appearance of important nonlinear structures and a system of two coupled nonlinear partial differential equations describing the spatio-temporal dynamics of a
predator-prey system where the prey per capita growth rate is subject to the Allee effect. The ![]() -
-
expansion method has been successfully used to find the exact traveling wave solutions of some nonlinear evolution equations. As an application, the traveling wave solutions for Dynamical system in a new Double- Chain Model of DNA and a diffuusive predator-prey system, which have been constructed using the ![]() -
-
expansion method. Let us compare between our results obtained in the present article with the well-known results obtained by other authors using different methods as follows: Our results of Dynamical system in a new Double-Chain Model of DNA and a diffusive predator-prey system, are new and different from those obtained in [37] -[41] and Figure 1 and Figure 2 show the solitary traveling wave solution of Dynamical system in a new
Double-Chain Model of DNA and a diffusive predator-prey system. It can be concluded that this method is reliable and proposes a variety of exact solutions NPDEs. The performance of this method is effective and can be applied to many other nonlinear evolution equations.
NOTES
*Corresponding author.