Nonlinear General Integral Control Design via Equal Ratio Gain Technique ()
1. Introduction
Integral control [1] plays an important role in practice because it ensures asymptotic tracking and disturbance rejection when exogenous signals are constants or planting parametric uncertainties appears. However, nonlinear general integral control design is not trivial matter because it depends on not only the uncertain nonlinear actions and disturbances but also the nonlinear control actions. Therefore, it is of important significance to develop the design method for nonlinear general integral control.
For general integral control design, there were various design methods, such as general integral control design based on linear system theory, sliding mode technique, feedback linearization technique and singular perturbation technique and so on, were presented by [2] -[5] , respectively. In addition, general concave integral control [6] , general convex integral control [7] , constructive general bounded integral control [8] and the generalization of the integrator and integral control action [9] were all developed by using Lyapunov method and resorting to a known stable control law. Equal ratio gain technique firstly was proposed by [10] , and was used to address the linear general integral control design for a class of uncertain nonlinear system.
All these general integral controllers above constitute only a minute portion of general integral control, and therefore lack generalization. Moreover, in consideration of the complexity of nonlinear system, it is clear that we can not expect that a particular integral controller has the high control performance for all nonlinear system. Thus, the generalization of general integral controller naturally appears since for all nonlinear system, we can not enumerate all the categories of integral controllers with high control performance. It is not hard to know that this is a very valuable and challenging problem, and equal ratio gain technique can be used to deal with this trouble since it is a powerful and practical tool to solve the nonlinear control design problem.
Motivated by the cognition above, this paper proposes a generic nonlinear integral controller and a practical nonlinear integral controller for a class of uncertain nonlinear system. The main contributions are that: 1) By defining two function sets, the generalization of general integral controller is achieved; 2) A canonical interval system matrix can be designed to be Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio; 3) Theorems to ensure regionally as well as semi-globally asymptotic stability is established in terms of some bounded information. Moreover, for the practical nonlinear integral controller, a real time method to evaluate the equal ratio coefficient is proposed such that its value can be chosen moderately. Theoretical analysis and simulation results demonstrated that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.
Throughout this paper, we use the notation 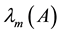 and
and 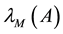 to indicate the smallest and largest eigenva- lues, respectively, of a symmetric positive define bounded matrix
to indicate the smallest and largest eigenva- lues, respectively, of a symmetric positive define bounded matrix , for any
, for any . The norm of vector x is
. The norm of vector x is
defined as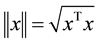 , and that of matrix A is defined as the corresponding induced norm
, and that of matrix A is defined as the corresponding induced norm .
.
The remainder of the paper is organized as follows: Section 2 describes the system under consideration, assumption and definition. Sections 3 and 4 present the generic and practical nonlinear integral controllers along with their design method, respectively. Example and simulation are provided in Section 5. Conclusions are presented in Section 6.
2. Problem Formulation
Consider the following controllable nonlinear system,
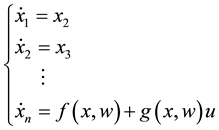 (1)
(1)
where  is the state;
is the state; 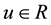 is the control input;
is the control input;  is a vector of unknown constant parameters and disturbances. The function
is a vector of unknown constant parameters and disturbances. The function 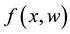 is the uncertain nonlinear action, and the uncertain nonlinear function
is the uncertain nonlinear action, and the uncertain nonlinear function  is continuous in
is continuous in  on the control domain
on the control domain . We want to design a control law
. We want to design a control law 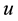 such that
such that 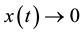 as
as![]() .
.
Assumption 1: There is a unique pair ![]() that satisfies the equation,
that satisfies the equation,
![]() (2)
(2)
so that ![]() is the desired equilibrium point and
is the desired equilibrium point and ![]() is the steady-state control that is needed to maintain equilibrium at
is the steady-state control that is needed to maintain equilibrium at![]() .
.
Assumption 2: Suppose that the functions ![]() and
and ![]() satisfy the following inequalities,
satisfy the following inequalities,
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
for all ![]() and
and![]() . where
. where![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are all positive constants.
are all positive constants.
Definition 1: ![]() with
with![]() ,
, ![]() and
and ![]() denotes the set of all continuous functions,
denotes the set of all continuous functions, ![]() such that
such that
![]()
and
![]()
hold for all ![]() and
and![]() . Where
. Where ![]() is a point on the line segment connecting
is a point on the line segment connecting ![]() to
to![]() .
.
Definition 2: ![]() with
with![]() , and
, and ![]() denotes the set of all integrable functions,
denotes the set of all integrable functions, ![]() such that
such that
![]()
and
![]()
hold for all![]() . Where
. Where ![]() is a point on the line segment connecting
is a point on the line segment connecting ![]() to the origin.
to the origin.
3. Generic Nonlinear Integral Control
The generic nonlinear integral controller is given as,
![]() (7)
(7)
where ![]() and
and ![]() belong to the function sets
belong to the function sets ![]() and
and![]() , respectively,
, respectively, ![]() ,
, ![]() and
and ![]() are all positive constants.
are all positive constants.
Thus, substituting (7) into (1), obtain the augmented system,
![]() (8)
(8)
By Assumption 1 and choosing ![]() to be large enough, and then setting
to be large enough, and then setting ![]() and
and ![]() of the system (8), obtain,
of the system (8), obtain,
![]() (9)
(9)
Therefore, we ensure that there is a unique solution![]() , and then
, and then ![]() is a unique equilibrium point of the closed-loop system (8) in the domain of interest. At the equilibrium point,
is a unique equilibrium point of the closed-loop system (8) in the domain of interest. At the equilibrium point, ![]() , irrespective of the value of
, irrespective of the value of![]() .
.
Now, by Definition 1, 2 and![]() ,
, ![]() and
and ![]() can be written as,
can be written as,
![]() (10)
(10)
![]() (11)
(11)
where ![]() and
and![]() .
.
Thus, substituting (9)-(11) into (8), obtain,
![]() (12)
(12)
where ![]()
![]()
And ![]() is an
is an ![]() matrix, all its elements are equal to zero except for
matrix, all its elements are equal to zero except for
![]()
Moreover, it is worthy to note that the function ![]() is integrated into
is integrated into ![]() via a change of variable. This has not influence on the results if the inequality (4) holds and it can be taken as
via a change of variable. This has not influence on the results if the inequality (4) holds and it can be taken as ![]() in the design. Therefore, it is omitted in all the following demonstrations.
in the design. Therefore, it is omitted in all the following demonstrations.
For analyzing the stability of closed-loop system (12), we must ensure that the matrix ![]() is Hurwitz for all
is Hurwitz for all![]() ,
, ![]() ,
, ![]() and
and![]() . This can be achieved by Routh’s stability criterion.
. This can be achieved by Routh’s stability criterion.
3.1. Hurwitz Stability
Hurwitz stability of the matrix ![]() can be achieved by Routh’s stability criterion, which is motivated by the idea [10] , as follows:
can be achieved by Routh’s stability criterion, which is motivated by the idea [10] , as follows:
Step 1: the polynomial of the matrix ![]() with
with ![]() is,
is,
![]() (13)
(13)
By Routh’s stability criterion, ![]() and
and ![]() can be chosen such that the polynomial (13) is Hurwitz for all
can be chosen such that the polynomial (13) is Hurwitz for all ![]() and
and![]() . Obviously, if
. Obviously, if ![]() and
and ![]() are all large to zero, and then the necessary condition, that is, the coefficients of the polynomial (13) are all positive, is naturally satisfied.
are all large to zero, and then the necessary condition, that is, the coefficients of the polynomial (13) are all positive, is naturally satisfied.
Step 2: based on the gains![]() ,
, ![]() and Hurwitz stability condition to be obtained by Step 1, the maximums of
and Hurwitz stability condition to be obtained by Step 1, the maximums of ![]() and
and![]() , that is,
, that is, ![]() and
and![]() , can be obtained, respectively. Since
, can be obtained, respectively. Since ![]() and
and ![]() interact, there exist innumerable
interact, there exist innumerable ![]() and
and![]() . Thus, two kinds of typical cases are interesting, that is, one is that
. Thus, two kinds of typical cases are interesting, that is, one is that ![]() is evaluated with
is evaluated with![]() ; another is that let
; another is that let![]() , and then
, and then ![]() can be obtained together.
can be obtained together.
Step 3: by ![]() and
and ![]() obtained by Step 2, check Hurwitz stability of the matrix
obtained by Step 2, check Hurwitz stability of the matrix ![]() for all
for all ![]() and
and![]() . If it does not hold, redesign
. If it does not hold, redesign ![]() and
and ![]() and repeat the previous steps until the matrix
and repeat the previous steps until the matrix ![]() is Hurwitz for all
is Hurwitz for all ![]() and
and![]() .
.
It is well known that Hurwitz stability condition is more and more complex as the order of the matrix ![]() increases. Thus, for clearly illustrating the design method above, we consider two kinds of cases, that is,
increases. Thus, for clearly illustrating the design method above, we consider two kinds of cases, that is, ![]() and
and![]() , respectively, as follows:
, respectively, as follows:
Case 1: for![]() , the polynomial (13) is,
, the polynomial (13) is,
![]() (14)
(14)
By Routh’s stability criterion, if![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are all positive numbers, and the following inequality,
are all positive numbers, and the following inequality,
![]() (15)
(15)
holds, and then the polynomial (14) is Hurwitz for all ![]() and
and![]() .
.
Sub-class 1:![]() ,
, ![]() and
and ![]() are multiplied by
are multiplied by![]() , and then substituting them into (15), obtain,
, and then substituting them into (15), obtain,
![]() (16)
(16)
By the inequality (16), obtain,
![]()
Sub-class 2:![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are multiplied by
are multiplied by![]() , and then substituting them into (15), obtain,
, and then substituting them into (15), obtain,
![]() (17)
(17)
For this sub-class, there are two kinds of cases:
1) if![]() , and then by the inequality (17), obtain,
, and then by the inequality (17), obtain,
![]()
2) if![]() , and then by the inequality (17), obtain,
, and then by the inequality (17), obtain,
![]()
Case 2: for![]() , the polynomial (13) is,
, the polynomial (13) is,
![]() (18)
(18)
By Routh’s stability criterion, if![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are all positive numbers, and the following inequality,
are all positive numbers, and the following inequality,
![]() (19)
(19)
holds, and then the polynomial (18) is Hurwitz for all ![]() and
and![]() .
.
Sub-class 1:![]() ,
, ![]() ,
, ![]() and
and ![]() are multiplied by
are multiplied by![]() , and then substituting them into (19), obtain,
, and then substituting them into (19), obtain,
![]() (20)
(20)
By the inequality (20), obtain,
![]()
Sub-class 2:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are multiplied by
are multiplied by![]() , and then substituting them into (19), obtain,
, and then substituting them into (19), obtain,
![]()
For this sub-class, although the situation is complex, a moderate solution can still be obtained, that is,
![]()
From the demonstration above, it is obvious that for![]() ,
, ![]() and
and ![]() or
or ![]() of the matrix
of the matrix![]() , there all exist
, there all exist ![]() such that the matrix
such that the matrix ![]() is Hurwitz for all
is Hurwitz for all![]() ,
, ![]() and
and![]() . Therefore, for the high order matrix
. Therefore, for the high order matrix![]() , the same result can be still obtained with the help of computer. Thus, we can conclude that the n+1-order matrix
, the same result can be still obtained with the help of computer. Thus, we can conclude that the n+1-order matrix ![]() can be designed to be Hurwitz for all
can be designed to be Hurwitz for all![]() ,
, ![]() ,
, ![]() and
and![]() .
.
Theorem 1: There exist ![]() and
and ![]() such that the system matrix
such that the system matrix ![]() for
for ![]() is Hurwitz, and then it is still Hurwitz for all
is Hurwitz, and then it is still Hurwitz for all ![]() and
and![]() .
.
Discussion 1: From the statements above, it is easy to see that: 1) the system matrix ![]() is an interval matrix; 2) in consideration of the controllable canonical form of linear system, the system matrix
is an interval matrix; 2) in consideration of the controllable canonical form of linear system, the system matrix ![]() can be called as the controllable canonical interval system matrix; 3) although Theorem 1 is demonstrated by the single variable system matrix
can be called as the controllable canonical interval system matrix; 3) although Theorem 1 is demonstrated by the single variable system matrix![]() , it is easy to extend Theorem 1 to the multiple variable case since Routh’s stability criterion applies to not only the single variable system matrix but also the multiple variable one. Thus, the following proposition can be established.
, it is easy to extend Theorem 1 to the multiple variable case since Routh’s stability criterion applies to not only the single variable system matrix but also the multiple variable one. Thus, the following proposition can be established.
Proposition 1: A canonical interval system matrix can be designed to be Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio.
3.2. Closed-Loop Stability Analysis
The matrix ![]() can be designed to be Hurwitz for all
can be designed to be Hurwitz for all![]() ,
, ![]() ,
, ![]() and
and![]() . Thus, by linear system theory, if the matrix
. Thus, by linear system theory, if the matrix ![]() is Hurwitz, and then for any given positive define symmetric matrix
is Hurwitz, and then for any given positive define symmetric matrix![]() , there exists positive define symmetric matrix
, there exists positive define symmetric matrix ![]() that satisfies Lyapunov equation
that satisfies Lyapunov equation![]() . Therefore, the solution of Lyapunov equation [11] is,
. Therefore, the solution of Lyapunov equation [11] is,
![]() (21)
(21)
where
![]() ,
,![]() and
and![]()
Thus, using ![]() as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop systems (12) is,
as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop systems (12) is,
![]() (22)
(22)
where![]() .
.
Now, using the inequalities (3), (5) and (6), obtain,
![]() (23)
(23)
where ![]() is a positive constant.
is a positive constant.
Substituting (23) into (22), and using![]() , obtain,
, obtain,
![]() (24)
(24)
By proposition proposed by [10] , that is, as any row controller gains, or controller and its integrator gains of a canonical system matrix tend to infinity with the same ratio, if it is always Hurwitz, and then the same row solutions of Lyapunov equation all tend to zero, we have,
1) ![]()
![]() as
as ![]()
2) ![]() as
as ![]()
where![]() .
.
Although there is innumerable![]() , the maximum
, the maximum ![]() exists and
exists and ![]() as
as![]() . Thus, there exist
. Thus, there exist ![]() with
with![]() , or
, or ![]() such that the following inequality,
such that the following inequality,
![]() (25)
(25)
holds for all ![]() with
with![]() , or
, or![]() . Therefore, we have
. Therefore, we have![]() .
.
Using the fact that Lyapunov function ![]() is a positive define function and its time derivative is a negative define function if the inequality (25) holds, we conclude that the closed-loop system (12) is stable. In fact,
is a positive define function and its time derivative is a negative define function if the inequality (25) holds, we conclude that the closed-loop system (12) is stable. In fact, ![]() means
means ![]() and
and![]() . By invoking LaSalle’s invariance principle, it is easy to know that the closed-loop system (12) is exponentially stable. As a result, the following theorem can be established.
. By invoking LaSalle’s invariance principle, it is easy to know that the closed-loop system (12) is exponentially stable. As a result, the following theorem can be established.
Theorem 2: Under Assumptions 1 and 2, if the system matrix ![]() is Hurwitz for all
is Hurwitz for all
![]() ,
,![]() ,
,
![]() and
and![]()
and then the equilibrium points ![]() and
and ![]() of the closed-loop system (12) is an exponentially stable for all
of the closed-loop system (12) is an exponentially stable for all
![]() with
with![]() , or
, or![]()
Moreover, if all assumptions hold globally, then it is globally exponentially stable.
Remark 1: From the statements of Subsections 3.1 and 3.2, it is to see that: by extending equal ratio gain technique to a canonical interval system matrix and using Lyapunov method, the asymptotic stability of the uncertain nonlinear system with generic nonlinear integral control can be ensured in terms of some bounded information. This shows that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.
Discussion 2: From the statements above, it is obvious that: although the generalization of nonlinear general integral control is achieved by defining two function sets, there are two unavoidable drawbacks, that is, one is that the controller (7) is too generic such that it is shortage of pertinence; another is that it is difficulty to obtain the less conservative ![]() or
or ![]() such that it is shortage of practicability. All these mean that Theorem 2 has only theoretical significance and not practical significance. Therefore, a practical nonlinear integral controller along with a new design method is proposed to solve these troubles in the next Section.
such that it is shortage of practicability. All these mean that Theorem 2 has only theoretical significance and not practical significance. Therefore, a practical nonlinear integral controller along with a new design method is proposed to solve these troubles in the next Section.
4. Practical Nonlinear Integral Control
For making up the shortage indicated by Discussion 2, a practical nonlinear integral controller is given as,
![]() (26)
(26)
where![]() ,
, ![]() ,
,
![]() and
and ![]() are the slopes of the line segment connecting
are the slopes of the line segment connecting ![]() to the origin
to the origin![]() , and they are utilized to harmonize the actions of
, and they are utilized to harmonize the actions of ![]() in the controller and integrator, respectively.
in the controller and integrator, respectively. ![]()
![]() is used to attenuate the uncertain nonlinear action of
is used to attenuate the uncertain nonlinear action of![]() .
. ![]()
![]() is applied to improve
is applied to improve
the performance of integral control action. ![]()
![]() is used to reorganize the integrator
is used to reorganize the integrator
output.![]() ,
, ![]() and
and ![]() are all positive constants, and
are all positive constants, and![]() .
.
Assumptions 3: By the definition of the controller (26), it is convenient to suppose that the following inequalities,
![]() (27)
(27)
![]() (28)
(28)
hold for all![]() ,
, ![]() and
and![]() , where
, where ![]() and
and ![]() are all positive constants.
are all positive constants.
By the same way as Section 3, we have,
![]() (29)
(29)
where![]() ,
,
![]()
![]() is an
is an ![]() matrix, all its elements are equal to zero except for
matrix, all its elements are equal to zero except for
![]()
and the functions ![]() and
and ![]() are integrated into
are integrated into ![]() and
and![]() , respectively.
, respectively.
By the design method proposed by Subsection 3.1, the system matrix ![]() can be designed to be Hurwitz for all
can be designed to be Hurwitz for all![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]()
![]() . Thus, by linear system theory, there exists positive define symmetric matrix
. Thus, by linear system theory, there exists positive define symmetric matrix ![]() that satisfies Lyapunov equation
that satisfies Lyapunov equation ![]() for any given positive define symmetric matrix
for any given positive define symmetric matrix![]() . Therefore, we can utilize
. Therefore, we can utilize ![]() as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop system (29) is,
as Lyapunov function candidate, and then its time derivative along the trajectories of the closed-loop system (29) is,
![]() (30)
(30)
where![]() .
.
Now, using the inequalities (4), (5), (6), (27) and (28), obtain,
![]() (31)
(31)
where ![]() is a positive constant.
is a positive constant.
Substituting (31) into (30), obtain,
![]() (32)
(32)
By proposition proposed by [10] (details see Subsection 3.2), for any moment![]() , there exists
, there exists ![]() with
with![]() , or
, or ![]() such that the inequality,
such that the inequality,
![]() (33)
(33)
holds for all ![]() with
with![]() , or
, or![]() . Consequently, if
. Consequently, if
the inequality (33) holds for all![]() , and then we conclude that
, and then we conclude that ![]() holds uniformly in
holds uniformly in![]() .
.
Using the fact that Lyapunov function ![]() is a positive define function and its time derivative is a negative define function if the inequality (33) holds for all
is a positive define function and its time derivative is a negative define function if the inequality (33) holds for all![]() , we conclude that the closed-loop system (29)
, we conclude that the closed-loop system (29)
is stable. In fact, ![]() means
means ![]() and
and![]() . By invoking LaSalle’s invariance principle, it is easy
. By invoking LaSalle’s invariance principle, it is easy
to know that the closed-loop system (29) is uniformly exponentially stable. As a result, we have the following theorem.
Theorem 3: Under Assumptions 1, 2 and 3, if the system matrix ![]() is Hurwitz for all
is Hurwitz for all
![]() ,
,![]() ,
,![]() ,
,![]() and
and![]()
and then the equilibrium point ![]() and
and ![]() of the closed-loop system (29) is uniformly exponentially stable for all
of the closed-loop system (29) is uniformly exponentially stable for all
![]() with
with![]() , or
, or![]()
Moreover, if all assumptions hold globally, and then it is globally uniformly exponentially stable.
Now, the design task is to provide a method to evaluate the instantaneous value ![]() with
with![]() , or
, or![]() . To achieve this objective, the procedure can be summarized as follows:
. To achieve this objective, the procedure can be summarized as follows:
Firstly, by the definitions of ![]() and
and![]() , the instantaneous values
, the instantaneous values ![]() and
and ![]() can be given as,
can be given as,
![]()
and
![]()
Secondly, by the inequality (33), the impermissible minimum of ![]() is,
is,
![]()
Finally, by the limitation conditions,
![]() with
with![]() , or
, or![]()
and the iterative method to solve Lyapunov equation,
![]()
![]() with
with![]() , or
, or ![]() can be obtained.
can be obtained.
Discussion 3: From the statements above, it is easy to see that: 1) all the component of the nonlinear integral controller (26) have the clear actions; 2) ![]() is not greater than
is not greater than ![]() since
since ![]() can be used to attenuate the
can be used to attenuate the
uncertain nonlinear action of ![]() and
and ![]() can be designed moderately; 3)
can be designed moderately; 3) ![]()
or ![]() is less conservative since they are all evaluated by the instantaneous values
is less conservative since they are all evaluated by the instantaneous values ![]() and
and![]() . All these not only solve the problem indicated by Discussion 2 but also mean that equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.
. All these not only solve the problem indicated by Discussion 2 but also mean that equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.
5. Example and Simulation
Consider the pendulum system [1] described by,
![]()
where![]() ,
, ![]() is the angle subtended by the rod and the vertical axis, and
is the angle subtended by the rod and the vertical axis, and ![]() is the torque applied to the pendulum. View
is the torque applied to the pendulum. View ![]() as the control input and suppose we want to regulate
as the control input and suppose we want to regulate ![]() to
to![]() . Now, taking
. Now, taking![]() ,
, ![]() , the pendulum system can be written as,
, the pendulum system can be written as,
![]()
and then it can be verified that ![]() is the steady-state control that is needed to maintain equilibrium at the origin.
is the steady-state control that is needed to maintain equilibrium at the origin.
By the practical nonlinear integral controller (26), the control law can be given as,
![]()
Thus, it is easy to obtain![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , and then the closed-loop system can be written as,
, and then the closed-loop system can be written as,
![]()
where![]() ,
,
![]()
and
![]()
The normal parameters are ![]() and
and![]() , and in the perturbed case,
, and in the perturbed case, ![]() and
and ![]() are reduced to 1
are reduced to 1
and 5, respectively, corresponding to double the mass. Thus, we have![]() .
.
Now, with![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() , the following inequality,
, the following inequality,
![]()
holds for all![]() , and then the matrix
, and then the matrix ![]() is Hurwitz for all
is Hurwitz for all![]() . Consequently, taking
. Consequently, taking ![]() as the initial value, the simulation is implemented under the normal and perturbed cases, respectively. Moreover, in the perturbed case, we consider an additive impulse-like disturbance
as the initial value, the simulation is implemented under the normal and perturbed cases, respectively. Moreover, in the perturbed case, we consider an additive impulse-like disturbance ![]() of magnitude 60 acting on the system input between 15 s and 16 s.
of magnitude 60 acting on the system input between 15 s and 16 s.
Figure 1 and Figure 2 showed the simulation results under normal (solid line) and perturbed (dashed line) cases. The following observations can be made: 1) The instantaneous value ![]() holds for all
holds for all![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and![]() . This shows that the closed-loop system is uniformly asymptotic stable and the equal ratio coefficient can be used to improve the conservatism. 2) The system responses are almost identical before the additive impulse-like disturbance appears. This means that by equal ratio gain technique, we can tune a nonlinear general integral controller with good robustness and high control performance. All these demonstrate that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.
. This shows that the closed-loop system is uniformly asymptotic stable and the equal ratio coefficient can be used to improve the conservatism. 2) The system responses are almost identical before the additive impulse-like disturbance appears. This means that by equal ratio gain technique, we can tune a nonlinear general integral controller with good robustness and high control performance. All these demonstrate that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.
![]()
Figure 1. The values of ![]() under normal (solid line) and perturbed case (dashed line).
under normal (solid line) and perturbed case (dashed line).
![]()
Figure 2. System output under normal (solid line) and perturbed case (dashed line).
6. Conclusions
This paper proposes a generic nonlinear integral controller and a practical nonlinear integral controller for a class of uncertain nonlinear system. The main contributions are that: 1) By defining two function sets, the generalization of general integral controller is achieved; 2) A canonical interval system matrix can be designed to be Hurwitz as any row controller gains, or controller and its integrator gains increase with the same ratio; 3) Theorems to ensure regionally as well as semi-globally asymptotic stability are established in terms of some bounded information. Moreover, for the practical nonlinear integral controller, a real time method to evaluate the equal ratio coefficient is proposed such that its value can be chosen moderately.
Theoretical analysis and simulation results demonstrated that not only nonlinear general integral control can effectively deal with the uncertain nonlinear system but also equal ratio gain technique is a powerful and practical tool to solve the control design problem of dynamics with the nonlinear and uncertain actions.