Performance of Suboptimal Controllers for Affine-Quadratic Problems ()
1. Introduction
One of the most active areas in control theory is optimal control and methods to find them [1] - [3] . It has a wide range of practical applications in engineering (Aerospace, Chemical, Mechanical, Electrical), science (Physics, Biology), and economics (see e.g. [4] - [7] ). Optimal control theory has been developed for linear systems ( [1] [2] [8] ) and explicit formulae for computing optimal control inputs are available. However, control of nonlinear systems is much more challenging and obtaining formulae for optimal controls seems in general not possible. This motivated researchers to study various classes of nonlinear control problems separately, and affine-qudratic problems is one such class. In a recent paper [9] , the optimal control for affine-quadratic problems is obtained in terms of the associated costate. But, in practice, it is difficult to compute the costate (at each time ) as the knowledge of its terminal condition is required.
) as the knowledge of its terminal condition is required.
In this article, we study the affine-quadratic control problem given by ((1), (2)). We note that a method for finding the initial condition for the costate is recently proposed [10] . This allows one to compute the initial costate (at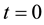 ) exactly or approximately. This approximation of the initial costate and the explicit formula for optimal control (as in [11] ) are shown, in this article, which give rise to suboptimal controls of practical importance. More precisely, our main theorem (Theorem 2) provides an upper bound for the difference in performance between these suboptimal and optimal control.
) exactly or approximately. This approximation of the initial costate and the explicit formula for optimal control (as in [11] ) are shown, in this article, which give rise to suboptimal controls of practical importance. More precisely, our main theorem (Theorem 2) provides an upper bound for the difference in performance between these suboptimal and optimal control.
The article is organized as follows. In Section 2, the affine-quadratic control problem is described. We also explain how to obtain the optimal control in terms of costate. The main (Theorem 2) is proved in Section 3. This theorem provides a method to obtain the costate (without the knowledge of its terminal value) which results in an explicit formula and performance bounds for a class of suboptimal controls.
Notation: For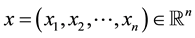 ,
, 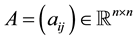 , and
, and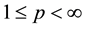 , we use the notation
, we use the notation
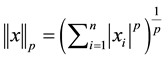 ,
,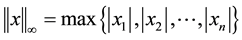 ,
,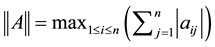 .
.
2. Problem Description
We consider the affine control system
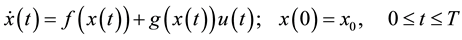 , (1)
, (1)
with the quadratic cost functional
 . (2)
. (2)
Here 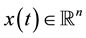 is the state vector,
is the state vector, 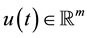 is the control vector,
is the control vector, 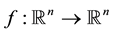 ,
,
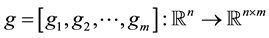 ,
, 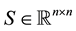 ,
, 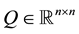 ,
, 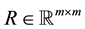 , and ' denotes transposition.
, and ' denotes transposition.
Throughout this paper, it is assumed that  are positive semidefinite,
are positive semidefinite, ![]() is positive definite, the functions
is positive definite, the functions ![]() are continuously differentiable with bounded derivatives, the control input
are continuously differentiable with bounded derivatives, the control input ![]() is chosen
is chosen
from the admissible control space![]() .
.
Under these assumptions, for each admissible control ![]() there exist a unique solution (trajectory) of
there exist a unique solution (trajectory) of
the control system (1) denoted by![]() .
.
The value function of the control problem given by (1), (2), is defined as
![]() .
.
A control input ![]() is optimal (for
is optimal (for![]() ) if
) if
![]() .
.
Similarly a control input ![]() is
is ![]() -optimal (for
-optimal (for![]() ) if
) if
![]() .
.
Given![]() , the optimal control problem is to find a control
, the optimal control problem is to find a control ![]() which minimizes the cost functional
which minimizes the cost functional
![]() . The Hamiltonian associated with the optimal control problem (1), (2), is given as
. The Hamiltonian associated with the optimal control problem (1), (2), is given as
![]() , (3)
, (3)
where ![]() is the adjoint vector.
is the adjoint vector.
To derive an expression for the optimal control ![]() (for
(for![]() ), it is convenient to introduce the adjoint
), it is convenient to introduce the adjoint
system:
![]() . (4)
. (4)
Here![]() . We now state the Pontryagin’s Minimum Principle (PMP) for the affine-quadratic
. We now state the Pontryagin’s Minimum Principle (PMP) for the affine-quadratic
control system (1), (2), which provides a set of necessary conditions for ![]() to be optimal [12] .
to be optimal [12] .
Theorem 1 [PMP] Let![]() ,
, ![]() , and
, and![]() . Also let
. Also let ![]() be the adjoint vector
be the adjoint vector
corresponding to ![]() and
and![]() , as given by the equation (4). Then for a control input
, as given by the equation (4). Then for a control input ![]() to be optimal
to be optimal
for![]() , it is necessary that the map
, it is necessary that the map
![]() ,
,
attains minimum at![]() , for a.e.
, for a.e.![]() .
.
Corollary 1 Let![]() ,
, ![]() , and
, and![]() . Also let
. Also let ![]() be the adjoint vector
be the adjoint vector
corresponding to ![]() and
and![]() , as given by the equation (4). Then the optimal control (for
, as given by the equation (4). Then the optimal control (for![]() ) is
) is
![]() . (5)
. (5)
Proof. The proof follows immediately from the above theorem. □
Now to obtain ![]() (in (5)) in terms of
(in (5)) in terms of![]() , we solve the coupled systems given in (1) and (4)
, we solve the coupled systems given in (1) and (4)
together with the initial conditions ![]() and
and ![]() respectively.
respectively.
In general, solving this coupled system and finding a closed form solution ![]() is very difficult. However
is very difficult. However
it may be easier to find ![]() approximately. Such an approximation
approximately. Such an approximation ![]() will lead to the associated adjoint state
will lead to the associated adjoint state
![]() and admissible control
and admissible control![]() . In the next section, we provide bounds for the
. In the next section, we provide bounds for the
difference between the performance indices corresponding to ![]() and
and![]() .
.
3. Performance of suboptimal controllers
In this section, we prove the main result.
Theorem 2 Consider the affine-quadratic control problem (1), (2). Let![]() ,
, ![]() be the optimal
be the optimal
control as given in (5), ![]() , and
, and ![]() be the adjoint vector corresponding to
be the adjoint vector corresponding to ![]() and
and![]() .
.
Also let ![]() be a suboptimal control and
be a suboptimal control and ![]() be the solution of the coupled system ((1), (4)) with
be the solution of the coupled system ((1), (4)) with
initial condition![]() . Then
. Then
![]() ,
,
where
![]()
The constant ![]() depends only on the matrix function
depends only on the matrix function ![]() and the constant
and the constant ![]() depends only on its gra- dient.
depends only on its gra- dient.
Proof. Note that
![]()
(6)
From R.H.S. of (6), we first consider the term
![]() .
.
By adding and subtracting ![]() inside the integral, we get
inside the integral, we get
![]()
Therefore
![]() . (7)
. (7)
From R.H.S. of (6), we next consider the term
![]() .
.
In a similar manner (as for (7)), we have
![]() . (8)
. (8)
From R.H.S. of (6), we next consider the term
![]() .
.
Let us have
![]()
In the above term, put the ![]() matrix
matrix ![]() as
as ![]() and the
and the ![]() matrix
matrix
![]() as
as ![]() for each
for each![]() . Then we have,
. Then we have,
![]()
Now using assumption on the matrix function![]() , we have that the matrix function
, we have that the matrix function ![]() is continuously differentiable and has bounded derivatives. Therefore
is continuously differentiable and has bounded derivatives. Therefore
![]()
Using this and following the procedure as for the inequality (7), we get
![]()
Therefore
![]() . (9)
. (9)
Hence the result follows by the inequalities (7), (8), and (9). □
Remark 3 It follows from the previous theorem that![]() , when
, when![]() .
.
This implies that ![]() is a good suboptimal control when
is a good suboptimal control when ![]() is a good approximation of
is a good approximation of
![]() . We emphasize the fact that
. We emphasize the fact that ![]() (and hence
(and hence![]() ) can be computed at each time
) can be computed at each time ![]() as
as ![]() is known.
is known.