Generalizations of Rough Functions in Topological Spaces by Using Pre-Open Sets ()
1. Introduction
Rough set theory [1], is an extension of set theory for the study of intelligent systems characterized by inexact, uncertain or insufficient information. Moreover, this theory may serve as a new mathematical tool to soft computing besides fuzzy set theory [2-4], and has been successfully applied in machine learning, information sciences, expert systems, data reduction, and so on. Recently, lots of researchers are interested to generalize this theory in many fields of applications [5-7]. In classical rough set theory, partition or equivalence (indiscernibility) relation is an important and primitive concept. But, partition or equivalence relation is still restrictive for many applications. To study this issue, several interesting and meaningful generalizations to equivalence relation have been proposed in the past, such as tolerance relations [8], topological bases and subbases [9-12]. Particularly, some researchers have used coverings of the universe of discourse for establishing the generalized rough sets by coverings [13]. Others [14-16] combined fuzzy sets with rough sets in a fruitful way by defining rough fuzzy sets and fuzzy rough sets. Furthermore, another group has characterized a measure of roughness of a fuzzy set making use of the concept of rough fuzzy sets [17-19]. They also suggested some possible real world applications of these measures in pattern recognition and image analysis problems. Some results of these generalizations are obtained about rough sets and fuzzy sets in [20-22].
Topological ideas are present not only in almost all areas of today mathematics, for example biochemistry [23] information systems [24] and others for more fields of topology applications [25] and its related links. The subject of topology itself consists of several different branches such as point set topology, algebraic topology and differential topology which have relatively little in common this richness of applications and differentiate between branches of topology implied a difficult to give an accurate definition for topology. The topology concepts like continuity, irresoluteness, compactness, connectedness, convergence, denseness and others are as basic to mathematicians. The topology structure τ on a set X is a general tool for constructing the above concepts. This tool contains many classes of near open sets such as: regular open [26], semi open sets [27], pre-open sets [28], β-open sets [29] and b-open sets [30]. Many authors used the previous types of near open sets to introduce some types of near continuous functions such as: In [28] the concept of pre-continuous functions are introduced. In [31] the concept of α-continuous functions is introduced.
The pair of lower and upper approximation operators is just a pair of interior and closure operators of a topology [32-34]. In [35] the concept of rough functions is introduced. In [35,36] we found the definition of the rough real number. In this paper, we propose to give a further study on rough functions and to introduce some concepts based on rough functions. In the beginning we will study rough sets on the real line.
In Section 2, we will initiate the notion of rough real functions. The aim of Section 3 is to define and study the new notion of “topological pre-rough function”. The main goal of Section 4 is to initiate and study the pre-approximations of a function as a relation. Finally, we aim in Section 5 to define an alternative description of the topological pre-rough functions and topological pre-rough continuity.
A topological space [36] is a pair  consisting of a set X and family τ of subsets of X satisfying the following conditions:
consisting of a set X and family τ of subsets of X satisfying the following conditions:
1)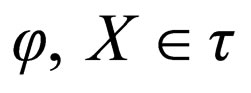 .
.
2) τ is closed under arbitrary union.
3) τ is closed under finite intersection.
The pair  is called a topological space, the elements of X are called points of the space, the subsets of X belonging to are called open set in the space, and the complement of the subsets of X belonging to τ be called closed set in the space; the family τ of open subsets of X is also called a topology for X.
is called a topological space, the elements of X are called points of the space, the subsets of X belonging to are called open set in the space, and the complement of the subsets of X belonging to τ be called closed set in the space; the family τ of open subsets of X is also called a topology for X.
 is called τ-closure of a subset
is called τ-closure of a subset .
.
Evidently, A is the smallest closed subset of X which contains A. Note that A is closed iff .
.
 is called the τ-interior of a subset
is called the τ-interior of a subset .
.
Evidently, 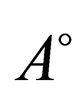 is the union of all open subsets of X which containing in A. Note that A is open iff
is the union of all open subsets of X which containing in A. Note that A is open iff . And
. And  is called the τ-boundary of a subset
is called the τ-boundary of a subset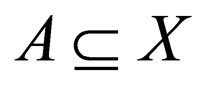 .
.
Let A be a subset of a topological space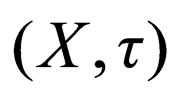 . Let
. Let ,
,  and
and  be closure, interior, and boundary of A respectively.
be closure, interior, and boundary of A respectively.  is exact if
is exact if , otherwise A is rough. It is clear
, otherwise A is rough. It is clear  is exact iff
is exact iff .
.
Definition 1.1: A subset A of a topological space  is called pro-open if
is called pro-open if .
.
The family of all pre-open sets of  is denoted by
is denoted by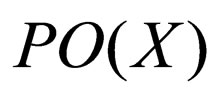 . The complement of pre-open set is preclosed set. The family of preclosed sets is denoted by
. The complement of pre-open set is preclosed set. The family of preclosed sets is denoted by .
.
Definition 1.2: A function  is said to be pre-continuous if
is said to be pre-continuous if  for every
for every  [28].
[28].
2. Rough Functions on Real Line
Let  be the set of non-negative real numbers, and let
be the set of non-negative real numbers, and let 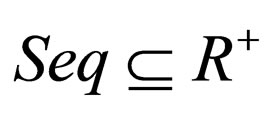 be a sequence of real numbers defined by
be a sequence of real numbers defined by  such that
such that . The sequence
. The sequence  defines the partition
defines the partition  of
of  by
by , where
, where 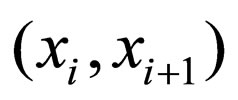 denote open intervals
denote open intervals . The sequence
. The sequence  is called a categorization of
is called a categorization of 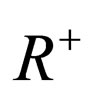 and the ordered pair
and the ordered pair  is an approximation space, where
is an approximation space, where  is the equivalence relation associated with
is the equivalence relation associated with .
.
Let  be an approximation space. By
be an approximation space. By  in
in  we denote the block of the partition
we denote the block of the partition  containing x, in particular if
containing x, in particular if , we have
, we have ,
,  is the closure of
is the closure of  with respect to the usual topology on R. Let
with respect to the usual topology on R. Let  be an approximation space, by
be an approximation space, by 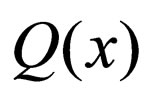 we denote the closed interval
we denote the closed interval  for
for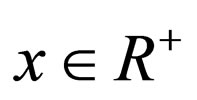 . For any
. For any , the seq-lower and the seq-upper approximations of
, the seq-lower and the seq-upper approximations of  in the approximation space
in the approximation space  are defined respectively by
are defined respectively by


The approximations of the closed interval  can be understood as the approximations of the real number
can be understood as the approximations of the real number  which are simply the ends of the interval
which are simply the ends of the interval . The number
. The number  is a rough number if
is a rough number if  , otherwise it is an exact number.
, otherwise it is an exact number.
Example 2.1: Let  be the set of all non-negative real numbers, and let
be the set of all non-negative real numbers, and let  be the set of natural numbers to be a sequence in
be the set of natural numbers to be a sequence in . Then the partition induced by
. Then the partition induced by  is
is  and hence,
and hence,  is an approximation space. Also, for any number
is an approximation space. Also, for any number , we have
, we have  and for any
and for any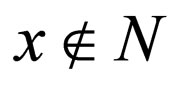 ,
,  and
and , Then every number
, Then every number  is a rough number in A.
is a rough number in A.
According to Example 1, we followed the following steps to get the approximations of a number , say
, say . We remark that the required approximations of
. We remark that the required approximations of  can be obtained directly in one step by
can be obtained directly in one step by .
.
Let X and Y be two subsets of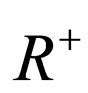 , and let
, and let  and
and  be two approximation spaces, where
be two approximation spaces, where  and P are equivalence relations on X and Y, respectively,
and P are equivalence relations on X and Y, respectively,  is a function. Then we define
is a function. Then we define  -lower approximation of
-lower approximation of  as the function
as the function , such that
, such that  for every
for every , and (S, P) -upper approximation of f as the function
, and (S, P) -upper approximation of f as the function , such that
, such that , for every
, for every .
.
We see that the term  in the above definition can be replaced by P only since the approximations of the function f depends only on P.
in the above definition can be replaced by P only since the approximations of the function f depends only on P.
Let  be a real valued function, where X and Y are two subsets of
be a real valued function, where X and Y are two subsets of . The function f is called a rough function at a point
. The function f is called a rough function at a point  if and only if
if and only if 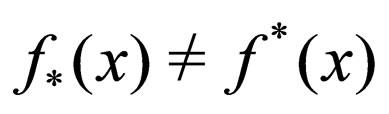 and f is called a rough function on X if it is a rough function at every point
and f is called a rough function on X if it is a rough function at every point .
.
We give the following example to indicate the above notions.
Example 2.2: Let  be a real valued function defined by
be a real valued function defined by 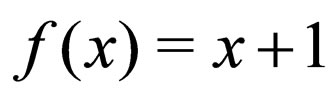 for every
for every . We denote the odd and even integers by O and E, respectively, then
. We denote the odd and even integers by O and E, respectively, then  and
and 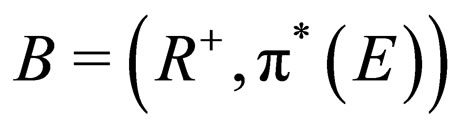 are approximation spaces, where
are approximation spaces, where 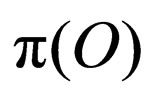 and
and  are partitions of
are partitions of  defined by
defined by  and
and , then at every point
, then at every point  we define E-lower approximation of f by
we define E-lower approximation of f by  such that
such that

and the E-upper approximation of f by the function  such that
such that . For
. For , we have
, we have , then
, then

and . Then f is an exact function at
. Then f is an exact function at , similarly we can prove that f is an exact functional at every odd natural number.
, similarly we can prove that f is an exact functional at every odd natural number.
For , then
, then

But

Then 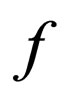 is a rough function at
is a rough function at , similarly it can be proved that
, similarly it can be proved that  is a rough function at every even natural number.
is a rough function at every even natural number.
Also, we notice that 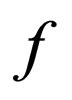 is a rough function at every
is a rough function at every . Then
. Then  is a rough function at every point
is a rough function at every point  or
or 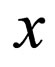 is an even natural number.
is an even natural number.
Let  be a real valued function. Then
be a real valued function. Then  is called
is called  -continuous (roughly continuous) at a point
-continuous (roughly continuous) at a point 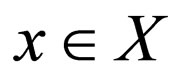 if
if , where
, where  and
and  are approximation spaces.
are approximation spaces.
Let  be a real valued function. Then
be a real valued function. Then  is roughly continuous on
is roughly continuous on  if
if  is a roughly continuous at every point
is a roughly continuous at every point .
.
Example 2.3: According to Example 2, the function  is a rough function at
is a rough function at  but
but 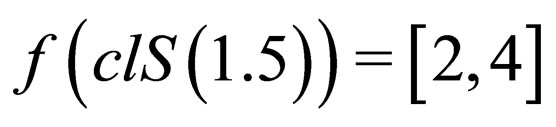 and
and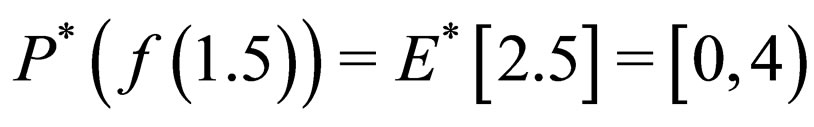 , then f is not a rough continuous function at the rough number
, then f is not a rough continuous function at the rough number , but at
, but at , since
, since 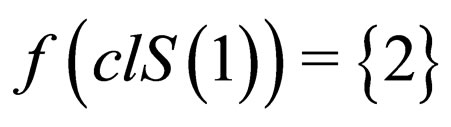 and
and  then f is a roughly continuous at
then f is a roughly continuous at , also at every
, also at every  such that x is odd number f is roughly continuous. If x is an even number, then f is not a roughly continuous; hence f is not a roughly continuous function on
such that x is odd number f is roughly continuous. If x is an even number, then f is not a roughly continuous; hence f is not a roughly continuous function on .
.
Example 2.4: Let X and Y be subsets of , such that
, such that  and
and  and the real valued function
and the real valued function  be defined by
be defined by ,
,  and
and , and consider the approximation spaces
, and consider the approximation spaces  and
and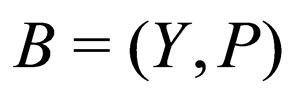 , where
, where  and
and  we define the function
we define the function  by
by . Then,
. Then,
 ,
,  ,
,
 ,
,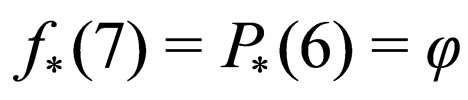 .
.
Also for the function  such that
such that
 . Then,
. Then,  ,
,
 ,
,  ,
,
 . Then the function f is P-rough at
. Then the function f is P-rough at  and f is not P-rough function at
and f is not P-rough function at .
.
Now, if , then
, then  and we have
and we have  and
and
 then
then , i.e., the function f is
, i.e., the function f is  -roughly continuous at
-roughly continuous at .
.
If , then
, then  and
and  , but
, but 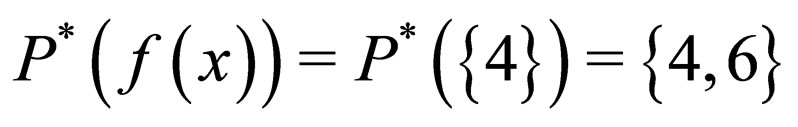 then, the function f is
then, the function f is  -roughly continuous at
-roughly continuous at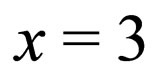 . Also at
. Also at  we find that f is
we find that f is  -roughly continuous, hence f is
-roughly continuous, hence f is  -roughly continuous on X.
-roughly continuous on X.
3. Topological Pre-Rough Functions
We purpose to generalize the concept of rough function to topological pre-rough function by using pre-open sets in topological spaces. Let  be a topological space and
be a topological space and . Then
. Then 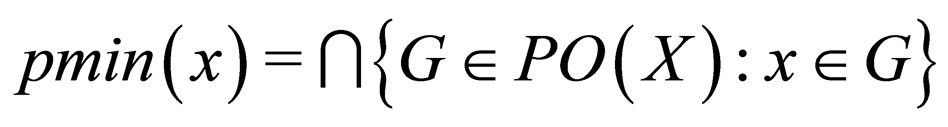 is called the pre minimal set containing the point
is called the pre minimal set containing the point  with respect to pre-open sets in the topology
with respect to pre-open sets in the topology  on X.
on X.
The principle topology on a set X is the topology has the minimal bases that consists only of minimal open sets at each .
.
Theorem 3.1: A topology  on a set X is principle iff arbitrary intersections of members of
on a set X is principle iff arbitrary intersections of members of  are members of
are members of  [20].
[20].
Let  be a principle topological space, for any element
be a principle topological space, for any element , we define pre-sequence by the set
, we define pre-sequence by the set  and by
and by  we mean the pre-closure of
we mean the pre-closure of  in
in .
.
If  is a function between principle spaces
is a function between principle spaces  and
and , we define the functions
, we define the functions , by
, by
 and
and  for every
for every , and
, and , by
, by  for all
for all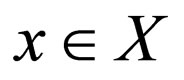 .
.
Let 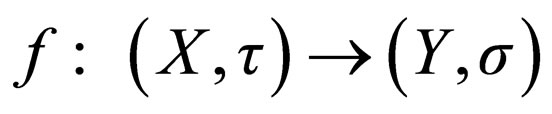 be a function, where X and Y are principle spaces. The function f is called a topological pre-rough function at the point x in X if and only if
be a function, where X and Y are principle spaces. The function f is called a topological pre-rough function at the point x in X if and only if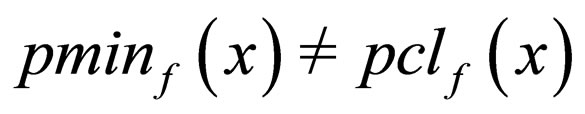 , and f is a topological pre-rough function on X if it is a topological pre-rough function at every point x in X.
, and f is a topological pre-rough function on X if it is a topological pre-rough function at every point x in X.
Example 3.1: Let  and
and  be topological spaces, where
be topological spaces, where ,
,
 and
and ,
,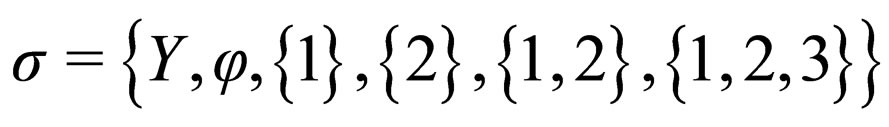 . Let
. Let  be a map defined by
be a map defined by ,
,  ,
,  and
and . We have the following table (Table 1).
. We have the following table (Table 1).
Consequently,  for every
for every , hence f is a topological pre-rough function on
, hence f is a topological pre-rough function on .
.
A function  is said to be a topological pre-rough continuous at the point
is said to be a topological pre-rough continuous at the point  if and only if
if and only if , and it is a topological pre-rough continuous on
, and it is a topological pre-rough continuous on  if it is a topological pre-rough continuous at every point
if it is a topological pre-rough continuous at every point .
.
Example 3.2: Let  and
and  be topological spaces, where
be topological spaces, where 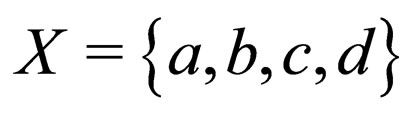 and
and  with
with  and
and
 . Let
. Let  be a map defined by
be a map defined by ,
,  ,
,  and
and 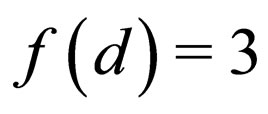 (Table 2).
(Table 2).
Consequently,  for every
for every , hence f is a topological pre-rough continuous function on X.
, hence f is a topological pre-rough continuous function on X.
4. The Pre-Approximations of Functions
A function f from X to  is a relation from
is a relation from  to
to  that satisfies:
that satisfies:
1) .
.
2) If  and
and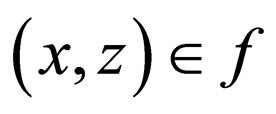 , then
, then .
.
If , we say
, we say  is a function on
is a function on . A function
. A function  is completely represented by its graph
is completely represented by its graph  .
.
The concept of rough relations is defined by using a certain type of relation products. The following proposition

Table 1.  and
and  for some subsets of X.
for some subsets of X.

Table 2. topological pre-rough continuous function on X.
will simplify the process of getting  via
via  and
and .
.
Theorem 4.1: Let  and
and  be a pre-approximation spaces. Then we have
be a pre-approximation spaces. Then we have  .
.
Proof: Since for any  and
and , we have,
, we have,  iff
iff  and
and
 . Let
. Let . Then we have
. Then we have

Hence .
.
Let  be any function, where
be any function, where  and
and  are pre-approximation spaces, such that
are pre-approximation spaces, such that  and
and 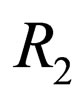 are equivalence relations on
are equivalence relations on 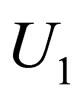 and
and  respectively. We define the equivalence relation
respectively. We define the equivalence relation  such that
such that
 is a partition of
is a partition of  for the function
for the function  we define the pre-approximations
we define the pre-approximations

 A function
A function 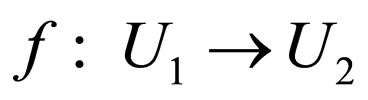 is said to be roughly in the pre-approximation space
is said to be roughly in the pre-approximation space , where
, where
 and
and  are pre-approximation spaces and
are pre-approximation spaces and ,
,  if
if
 otherwise f is pre-exact function.
otherwise f is pre-exact function.
Example 4.1: Let  and
and  and consider the function
and consider the function  defined by
defined by
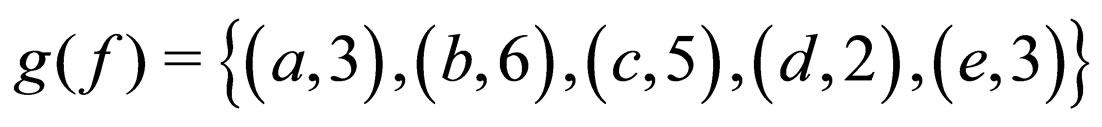 .
.
Consider the partitions  and
and . Then
. Then

is a partition of .
.
Then  and
and

Therefore the function f is a rough function such that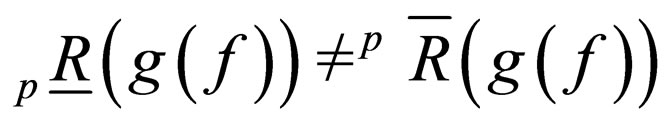 .
.
For the function , we observe that in general
, we observe that in general  and
and  are not functions from
are not functions from  into
into . We point that, the process of defining an pre-approximations on
. We point that, the process of defining an pre-approximations on  such that
such that 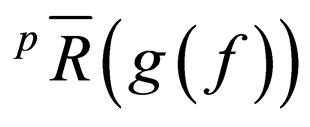 and
and  are functions is an open question to be solved in our next work.
are functions is an open question to be solved in our next work.
Theorem 4.2: For every function 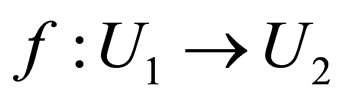 such that
such that  and
and  are selective preapproximation spaces then f is an pre-exact function.
are selective preapproximation spaces then f is an pre-exact function.
Proof: Since in any selective pre-approximation space,  then
then  then f is an preexact function.
then f is an preexact function.
Example 4.2: Let  and
and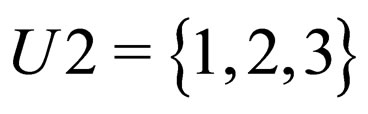 . Consider the function
. Consider the function , defined by
, defined by  =
= and consider the partitions
and consider the partitions
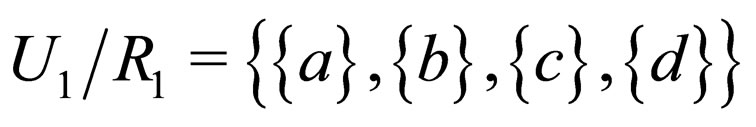 and
and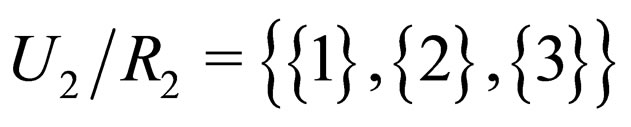 . Then
. Then
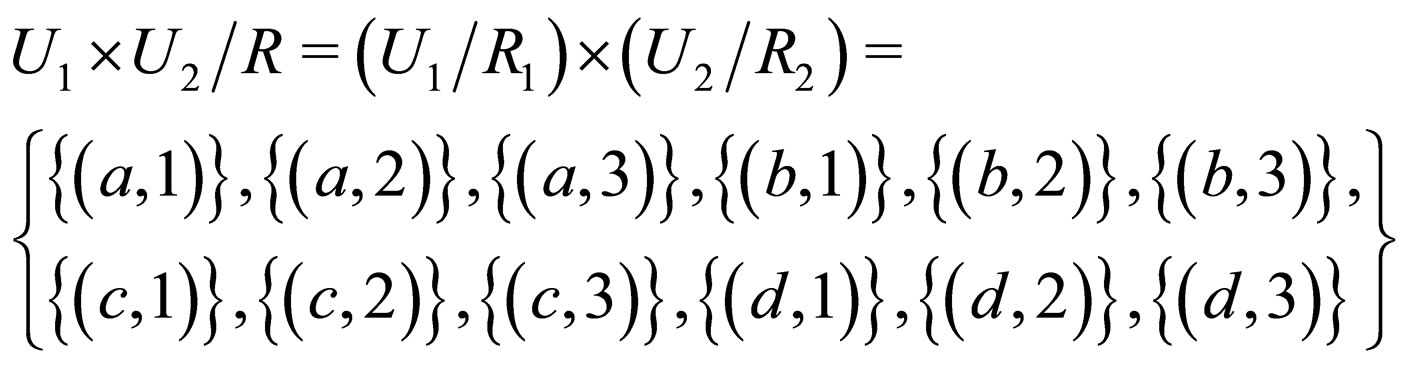
is a partition of .
.
Then 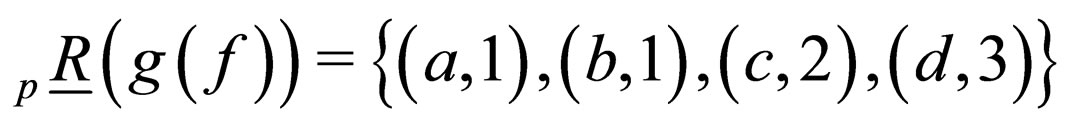 and
and  , then f is an pre-exact function.
, then f is an pre-exact function.
For a function 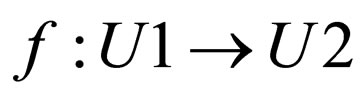 such that
such that  and
and  are selective pre-approximation spaces then 1) If f is a one-to-one function then also both
are selective pre-approximation spaces then 1) If f is a one-to-one function then also both 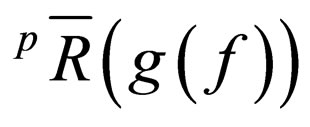 and
and .
.
2) If f is onto function then also both  and
and .
.
3) If f is a pre-continuous function then also both  and
and .
.
No function  such that
such that  and
and  are not selective approximation spaces is pre-exact, and f is not a constant function.
are not selective approximation spaces is pre-exact, and f is not a constant function.
5. An Alternative Description of Topological Pre-Rough Functions
Let 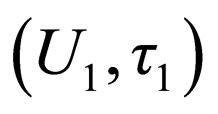 and
and  be any topological spaces, the function
be any topological spaces, the function , can be considered as a relation of
, can be considered as a relation of  and if
and if  is a basis of
is a basis of  and
and  is a basis of
is a basis of , then
, then  is a basis of the topology
is a basis of the topology  on
on . In the topology
. In the topology 
we define  and
and  for the function f. Let
for the function f. Let  be a function, where
be a function, where  and
and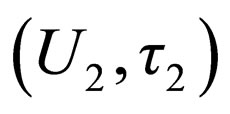 , are topological spaces, the function f is called a topological pre-rough function in
, are topological spaces, the function f is called a topological pre-rough function in  iff
iff  otherwise, f is an preexact function in
otherwise, f is an preexact function in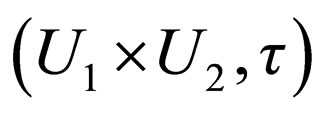 .
.
Example 5.1: Let  and
and 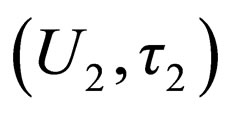 be any topological spaces where
be any topological spaces where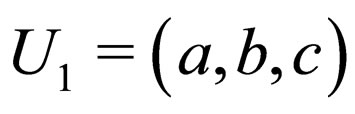 ,
,
 ,
,  ,
,
 Consider
Consider  and
and 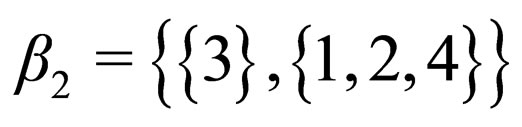 are basis of
are basis of  and
and  respectively. Let
respectively. Let ,
,  and
and  are mappings defined by
are mappings defined by
 ,
,

and .
.
Then  and
and

Then f is a pre-rough function in . Also,
. Also,  and
and 
We call g is a function not defined from pre-lower and from upper. Finally, for the constant function h, we have , and h is an pre-exact function. In fact, h is the only exact function in
, and h is an pre-exact function. In fact, h is the only exact function in .
.
According to Example 1, we have the following:
1) The function f is continuous, but  and
and  are not functioning, hence we cannot say that
are not functioning, hence we cannot say that  or f is pre-continuous.
or f is pre-continuous.
2) The function h is always precontinuous function, and it is an pre-exact function, hence  and
and  is pre-continuous functions.
is pre-continuous functions.
6. Experiments and Evaluations
This section shows the effectiveness of using pre-rough functions for extracting new data from multi-valued information systems.
In this section, we briefly describe the Rheumatic Fever datasets mentioned in [37] as a topological application of rough functions. As mentioned in [39] rheumatic fever is a very common disease and it has many symptoms differs from patient to another though the diagnosis is the same. So, we obtained the following example on four rheumatic fever patients. All patients are between 9-12 years old with a history of Arthurian began from age 3-5 years. This disease has many symptoms and it is usually started in young age and still with the patient along his life.
Table 3 in [37] introduced the seven patients characterized by 8 symptoms (attributes) using them to decide the diagnosis for each patient (decision attribute). Where the attributes are satisfied in Table 2 in [37].
We recall and sell it here Table 3.
If we defined the following mapping on Table 3:
 :
:
 ,
,
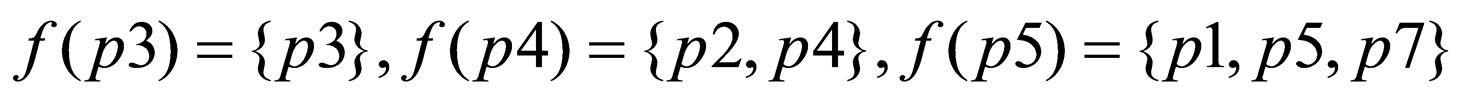

From the relation  where a is an element of the power set of the set of condition attributes
where a is an element of the power set of the set of condition attributes . The the following classes
. The the following classes  and
and 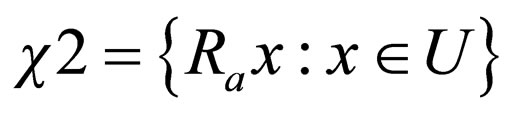 are two subbases of two topologies on U such that
are two subbases of two topologies on U such that  . Then according to Table 3 we have the following couples of topologies:
. Then according to Table 3 we have the following couples of topologies:
 ,
,









According to the mapping  and using each one of the above topologies we can deduce that the decision topology can be given by:
and using each one of the above topologies we can deduce that the decision topology can be given by:
 .
.
Now we can construct a familiar system of Table 3 contains only the pre-rough images constructed using the terminology of pre-rough functions. This system can be the reduction system of Table 3 and it given in Table 4.
This means that we can remove the conditional attribute  without any loss of information.
without any loss of information.
7. Conclusions
We conclude that the emergence of topology and its operators [38,39] in the construction of some rough set concepts will help to get rich results that yields a lot of logical statements which discover hidden relations between data and moreover, probably help in producing

Table 3. Multi-valued information system of [37].
accurate programs. These topological operators will play an essential role in data mining and knowledge discovery in databases. In this paper, we give an overview of several dissipated results on the pre-rough functions. More specifically, we attempt to show: usefulness of this new concept in a calculus of rough functions.
The future application of this work will be useful in many fields such as Fuzzy Expert Systems [40] by generalizations of rough functions for fuzzy rough functions. It also is useful in knowledge discovery methods [41].