Understanding the Relationships between Environmental and Social Risk Factors and Financial Performance of Global Infrastructure Projects ()
1. Introduction
Environmental and social risk factors are increasingly becoming part of the metrics used by investment professionals to analyse and value the financial loss associated with infrastructure projects they invest in. With increasing regulatory movement towards environmental and social responsibility, the lending financial institutions can be judged for being responsible for the borrower’s activities and treated as partakers in civil or criminal liability [1] . These financial institutions may also suffer because of the effect that ESR matters can have on borrower’s repayment ability of a loan and its security. Therefore it became apparent that financial institutions due to direct or indirect liability for ESR matters may experience loss of income. Moreover, this loss of income can even double in the event where both direct and indirect liabilities emerge simultaneously [2] .
Along with known environmental issues (e.g. waste disposal, carbon emissions, resource depletion, ecosystem change, etc.) social factors (such as worker rights, safety, child labour, human rights, community relations, etc.) play an increasingly important role in public’s and government’s perception of the listed companies. There are several ESR related transmission channels (suggested by Mark Hoff and Martin [3] ) through which infrastructure projects and hence investors can incur a financial loss.
First of all ignoring environmental and social concerns harms the reputation of the project and its investors by reducing project credibility. An increasing number of construction firms have adopted corporate social responsibility business approach aiming to enhance the brand image and improve financial performance [4] . In particular, they applied ISO 14000 series environmental management systems on a voluntary basis, providing organisations with a useful tool to manage the impact of each individual project on the environment [5] . Other construction firms became actively targeted by regulators requested to manage their performance according to the goals of sustainable development [6] . Zhao et al. [7] argue that the company which is considered socially responsible can benefit both by its enhanced reputation with the public, as well as its reputation within the business community, and at the same time increase its ability to attract capital and trading partners. Thus the incentives range from financial benefits to improved reputation in the community.
Secondly, rising public opposition can cause delays in the project realisation. This increases project costs and as the result lowers its financial performance. Infrastructure projects are rightfully referred as essential ingredients for productivity, output, or long-term growth of the modern economies [8] . At the micro level infrastructure usually, yields a significant social benefit and substantially improves the quality of life [9] . Nevertheless, each project still can encounter a resistance from local communities which impose the financial risk on investment by potentially delaying project implementation, increasing the cost of implementation, and undermining project viability [10] [11] . Why is this case? Generally, there always are stakeholders―groups of people whose lives or environment are affected by the project, but who receive no direct benefit from it [12] . Neglecting stakeholders’ concerns can impose a substantial risk on the viability of the project. For example Keystone XL pipeline in North America, the Belo Monte Dam in Brazil, and the Bujagali Dam in Uganda undergone substantial changes and incurred a financial loss due to public opposition [13] . In Europe, for example, motorway link Rijksweg A4 in the Netherlands, Eurotunnel between France and the UK also faced public opposition causing substantial project delays [3] . Noteworthy that in developed economies public opposition concerns focuses mainly on adverse health effects and environment protection, while in developing countries the focus is mainly on the land take, relocation and livelihoods impact [3] .
Thirdly, not complying with environmental and social performance standards set by Equator Principles Financial Institution may result in the withholding of funds or even blacklisting. For example one of the corporate investors (ING) stopped financing the construction of the Orion paper pulp mill project in Uruguay through the Equator Principles [14] . Equator Principles framework comprises a set of environmental and social guidelines that regulate finance transactions in global projects. Currently, there are more than 80 banks (holding about three-quarters of the project finance capital) who have adopted Equator Principles [15] . There still is an open question on whether the banks have implemented the principles properly as compliance by these banks is rather mixed [16] [17] [18] .
While there seem to be a degree of coherence in regards to ESR related transmission channels, the overall conclusion on the effect of specific ESR factors is not a clear cut. Thus in twenty academic studies ten suggested a positive relationship between ESR factors and portfolio performance [19] - [28] with seven reporting a neutral effect [29] - [35] and three reporting a negative relationship [36] [37] [38] . A numerous research points out the need to properly incorporate environmental and social risk management strategy in order to achieve a higher sustainable performance of the construction projects [39] [40] [41] [42] [43] . Failing to do so, most importantly during the project feasibility study, may have fatal consequences on the project financial performance [44] . Environmental and social laws will impose liabilities and constraints on a project, thus the cost of compliance can be significant [11] . On the other hand a company that is efficient in managing environmental and social issues might avoid unforeseen costs, violation of agreed delivery time terms and the budget. The study by Zhao et al. [7] also reveals a direct link between ESR issues and performance of the construction project.
Also at issuer level, the environmental and social performance is seen to have a long-term impact on corporate finance [45] [46] . The study by Bauer [47] explores 585 US corporate bonds issued during 1996 and 2005. It concludes that companies with poor environmental management incurred a higher cost of debt, lower bond and issuer ratings. This conclusion is consistent with research outcomes of Chava [48] and Schneider [49] . Studying corporate bonds, Bauer et al. [50] and Kane et al. [51] both suggested that stronger employee relations have a positive effect on the financial performance of a company and its capability to sustain finical distress. The research conducted by Swaffield and Johnson [52] established that there are direct and indirect financial benefits gained as a consequence of Implementing ISO 14,000 series (mainly related to environmental issues) at contraction sites.
One of the key problems that industry faces is the difficulty of obtaining the uniform data on ESR that can be measured. As the result, the balance sheets and income statements do not explicitly reflect these potential risks.
Our hypothesis regards the link between ESR concerns and risk-return profile of infrastructure bonds. We argue that the issuers with poor environmental practices are more likely to deteriorate the value of infrastructure bonds (for example due to a higher exposure to potentially costly environmental litigation, reputational losses, and regulatory risk) which results in a higher finical risk for the bond investors. Thereby the current study attempts to identify the ESR factors that impose the financial risk on the infrastructure project investor. To this end, the econometric analysis was conducted on the sample of global infrastructure bonds. The aspects of this analysis involve the use of additive regression models (with four-parameter flexible distribution) for modelling non-linear effects between the response variable (which accounts for the risk-return profile of a bond) and covariates (accounting for the bond and issuer specific characteristics, ESR related data, etc.).
The paper is organised as follows. Section 2 introduces the conceptual modelling framework adopted in the current study. Section 3 overviews the data set, describes data cleaning process and defines the variables. Section 4 introduces the model selection methodology and its modification developed to overcome certain data sample limitations of the current study. Section 5 presents modelling results. Section 6 discusses out-of-sample model validation and Section 7 concludes the paper.
2. Modelling Framework
In order to estimate the relationship between financial risk and ESR factors this study utilises a class of models known as General Adaptive Models of Location, Shape, and Scale (GAMLSS) [53] primarily for two main reasons.
First of all in GAMLSS the distribution of the response variable is not limited to exponential family (e.g. Normal distribution), instead, more general (e.g. highly skewed and/or kurtotic) distributions are allowed. This is particularity important in the context of non-normally distributed response variable used in this study. Moreover, GAMLSS capability for modelling up to four distribution parameters (which are usually associated with location, dispersion, skewness and kurtosis of distribution) can provide the estimates not only for the expectation itself but also for the balance of risk around it. In particular, this modelling framework is very efficient in detecting the presence of tail events, asymmetry of risks and non-linearity of effects.
Secondly, in GAMLSS all distribution parameters can be modelled as linear, non-linear, parametric and nonparametric additive functions of covariates. The utilisation of nonparametric additive functions is particularly important when the studied relationships are not known in advance (as for example in our study). Thus the GAMLSS framework allows for estimating a functional form of the non-linear relationship for each distribution parameter from the data without a need for prior specification of the exact mathematical form.
The generalised additive model for location, scale and shape can be expressed as follows:
where
denotes the vector of response variable elements distributed with probability density function
which is conditional on the vector of distribution parameters
;
are the matrices of the covariates and
are the regression parameters to be estimated,
are the smooth functions of covariates
for
and
while
are known monotonic link functions. Thus
denote parametric terms while
denote non-parametric terms (e.g. spline functions). Note the matrices
and covariates
may differ across distribution parameters.
The spline functions in this study are modelled using thin plate regression splines [54] . Thin plate splines constitute a method for selecting the degree of smoothing for spline function based on generalised Akaike information criteria (GAIC) [55] . Important to note that non-linear relationships (the case when the degree of spline function is above 1) can be reduced to linear relationships by smoothing algorithm if this facilitates a better model’s fit to the data.
3. Data
All the datasets used in the project are obtained from the Bloomberg database. Being a leading vendor of financial information, Bloomberg, from 2014 also provides an access to the environmental, social and governance (ESG) research assessments of a large number of the global companies. These ESG data cover the areas ranging from emissions and energy consumption to accident rates and governance structure. As all-in-one data terminal Bloomberg also provides functionality for linking bonds related information with ESG performance of selected companies. Thus, bonds were shortlisted as infrastructure related based on specification and content of ‘‘use of proceeds’’ document. This document discloses a detailed information for investors on how the invested funds will be used (usually provides a list of the projects to which bond proceeds will be allocated). The selected sample comprises bonds issued by both public and private issuers to finance 1) utilities, including power generation companies, electric and natural gas transmission and distribution networks, long-haul energy pipelines, water and wastewater companies, and integrated utilities; 2) transport systems, including roads, bridges, ports, airports and rail networks; 3) other fundamental facilities serving a country, city or other particular area, such as stadiums, military installations and hospitals.
This study adopts the Z-spread as a measure of the risk-return profile of infrastructure bonds. Z-spread can be defined as a continuously compounded static spread over the London Interbank Offered Rate (LIBOR) curve (if the bond is held to maturity) such that the discounted cash flows of the bond are equal to its current market price. In other words, Z-spread quantifies what the market thinks of the bond value [56] , thus making it a good measure for assessing the risk-return profile of different bonds.
Our study incorporates four sets of covariates (see Table 1), which account for 1) environmental and social risk; 2) macroeconomic conditions; 3) bond specific characteristics; and 4) issuer specific characteristics. We define environmental risk as the thread on living organisms and environment caused by emissions, wastes, resource depletion, etc. The social risk, besides environmental concerns (e.g., environmental degradation) can also be incurred by labour and human rights violations, corruption, marginalisation, social and economic stratification which disrupt or stop operations through strikes, sabotage, and violence. Social and environmental risks are well interconnected as one can emerge on the bedding of the other; therefore it is not usually possible to draw a clear line between the two. We select bond and issuer related covariates based on studies by Zmijewski [57] , Altman [58] . In order to account for some common pitfalls and risks to holding infrastructure bonds, we introduce a set of macroeconomic variables to our analysis.
The collected data consists of a list of infrastructure bonds issued by various companies across the globe with trading periods unique for each bond. The trading periods span from issue date of each bond to 1 November 2016 or bond’s maturity date (whichever is sooner). This results in unbalanced panel data that imposes certain modelling challenges in our study. To overcome that problem the data related to each bond was averaged over a number of years that bond was trading. Categorical binary variables (that alter by 0 or 1) were rounded to the nearest whole number after the averaging. All continuous environmental and social risk factors were divided by issuer’s tangible assets to form ratios in order to account for the asymmetry of environmental and social impacts due to the scale of the business. Finally, all continuous variables were centred and scaled
according to the following rule:
, in order to facilitate the fitting of a
probability distribution to a series of data.
As the result of non-reporting or lack of relevance for an industry group, there is a large amount of missing observations for the ESR-related and other covariates in the data. We anticipate that extrapolating the covariants beyond the
![]()
![]()
Table 1. Covariates used in the analysis.
original observations (to replace missing values) will not be particularly meaningful given the context of the data used in our study. Instead, we attempt to address this issue by tailoring a suitable model selection methodology.
4. Model Selection
This study employs the model selection procedure (discussed in Stasinopoulos et al. [55] ) in order to identify the model that is best supported by the data (referred to as parsimonious model). In particular, in GAMLSS the model selection is mainly concerned with selecting appropriate distribution for the response variable and the relevant covariates (e.g. risk factors) for distribution parameters. Moreover, it prevents overfitting, underfitting and addresses the causation problem to some degree. The model selection is performed based on the generalised Akaike information criteria (GAIC). That is the model with the smallest GAIC value is identified as the parsimonious model.
where GD is a global deviance of the model, df is a number of effective degrees of freedom of the fitted model and k is a specific penalty. For example
and
(where n is a sample size) correspond to Akaike information criterion [59] and Schwarz Bayesian criterion [60] accordingly.
First, we selected a flexible four-parameter JSU distribution which is a reparameterization of the original Johnson’s Su distribution [61] . Figure 1 illustrates the histogram of Z-spreads in the studied sample with fitted JSU and normal distribution probability functions. The vertical axis represents the frequency count, while the horizontal axis shows the range of scaled Z-spread values observed. A visual analysis suggests that the flexible JSU distribution fits the data better as, unlike normal distribution; it is able to capture skewness and excess kurtosis of the data. Moreover, despite its great flexibility, JSU distribution also offers excellent interpretability properties. Parameters
and
exactly define the mean (location) and standard deviation (scale) of the distribution, while the shape parameters
and
are associated with skewness and kurtosis of the distribution. This flexibility is expected to provide us with the better estimates of the balance of risk around the mean.
Secondly, the step-wise selection of covariates (schematically illustrated in Figure 2) is done in two stages―forward and backwards procedures. In the forward procedure, the algorithm iterates through distribution parameters and checks in sequence each covariate for inclusion into the model. It stops when none of the remaining covariates can further improve the GAIC score. This consecutive process may render some of the earlier included covariates non-significant. Thus in order to ensure that the model incorporates only significant variables the forward procedure is followed by the backwards procedure. In the backwards procedure, the earlier included covariates are checked again successively for the significance in order to be kept in or removed from the model.
Finally, when the best model is selected with the step-wise procedure discussed above, we refit this model by constructing an extra null space penalty
![]()
Figure 1. The Z-spread and the fitted JSU vs NO distribution.
![]()
Figure 2. Flowchart of the model selection strategy.
for each smooth function. This is an additional measure that guarantees that effects of insignificant covariates are penalised to zero and dropped out from the model.
All covariates listed in the Table 1 were supplied to the model selection algorithm discussed above. The algorithm has converged to the following parsimonious model:
where
is Z-spread of an infrastructure bond;
is a time to maturity;
is domestic base interest rate;
amount of carbon dioxide emission to tangible assets ratio;
is a dividend health of an issuer;
is a percentage of independent directors engaged;
is energy consumption to tangible assets ratio;
is a reparameterization of the original Johnson’s Su distribution;
is a smooth function of the covariates. Following a data-driven modelling approach in this study we do not assume any particular mathematical form of
in advance, instead, the form of
is estimated from the data.
The model diagnostic stage involves the use of worm plots [62] to justify an adequacy of the model. Worm plots are de-trended normal Q-Q plots of the quantile residuals (z-scores). Figure 3 contains the de-trended Q-Q plot for the JSU distribution of z-scores over the studied sample of bond Z-spreads. The normalised residuals (yellow dots on the Figure 3) are close to the origin and are located
![]()
Figure 3. Worm plot of residuals of fitted bond default model.
between dashed lines (95 percent confidence interval), indicating that the model is relatively adequate i.e. differences between the empirical and theoretical distributions are due to random variation only.
Matching all non-missing values of the selected covariates produced a sample of 142 infrastructure bonds issued by various companies across the globe from a range of industry sectors shown in Figure 4.
5. Modelling Results
This section provides a detailed interpretation on how the expected Z-spread and the balance of risk around it are conditioned on the ESR factors and other covariates.
Financial risk: m
The location parameter (m) characterises the expected Z-spread for a given bond. It provides the anticipated Z-spread in the long run and serves as one of the key measures for risk quantification. The model for location parameter is:
Thus the expected Z-spread is directly affected by the time to maturity of a bond, base interest rate, level of carbon dioxide emission to tangible assets ratio, dividend health of an issuer, a percentage of independent directors engaged and various interactions of these covariates. The effects can be disintegrated as follows:
![]()
Figure 4. Distribution of infrastructure bonds by country and industry sector in the studied sample.
: Time to maturity has a positive linear effect on the expected Z-spread (see Figure 5 TTM plot) with the marginal effect equal to 0.018. This overall fits the theory suggesting that spreads widen as maturities lengthen among the bonds (e.g. Beaumont [63] ).
: The base interest rate has a positive linear effect on the expected Z-spread (see Figure 5 INT plot) with the marginal effect equal to 0.034. This kind of relationship between credit spreads and interest rate is associated with periods of an economic slowdown. Noteworthy that 76% of the infrastructure bonds in the studied sample were issued and actively traded after the year 2007, thus covering the finical crisis and subsequent recovery period.
: The level of CO2 emission to tangible assets ratio has a positive linear effect on the expected Z-spread (see Figure 5 CO2 plot) with the marginal effect equal to 0.006. Thus we observe a higher expected Z-spread for the issuers that have high CO2 to tangible assets ratio. The financial risk contribution from CO2 emission to tangible assets ratio in our sample is the highest on average for the companies from Energy, Utilities and Consumer Cyclical sectors which are indeed associated with higher (comparing to other sectors) CO2 output. Theretofore CO2 emission on top of being one of the key contributors to undesired environmental changes is also associated with higher financial risk in the area of infrastructure development.
: The effect of issuer’s dividend health on the expected Z-spread is an inverted U-shaped relationship (see Figure 5 CRH plot) with the marginal effect equal to −0.002. This dynamics is sensible and generally fits insights from multiple studies (e.g. Litterman and Iben [64] , Bhojraj and Sengupta [65] , etc).
: The percentage of independent directors has a positive linear effect on the expected Z-spread (see Figure 5 IDIR plot) with the marginal effect equal to 0.007. Independent directors are not employees of the firm, they neither
![]()
Figure 5. Partial effect of
terms (
―time to maturity,
―base interest rate,
―level of carbon dioxide emissions to tangible assets ratio,
―dividend health of an issuer, and
―percentage of independent directors) on the expected Z-spread.
own company’s shares nor have any material relationship with the firm. Independent directors monitor the company to ensure that executives act also in the interest of shareholders. In general, the research evidence on the effectiveness of independent directors is not a clear cut, indicating both positive and negative aspects of this role in regards to firm’s financial performance (e.g. Bhagat and Black [66] , Knyazeva et al. [67] , etc). Also, the percentage of serving independent directors varies greatly across various states. Thus the average percentage of independent directors is the highest for the US based companies (about 89%) and lowest for Japanese companies (about 18%). Perhaps a better approach would be estimating the partial effect of independent directors with the reference to a domestic country. However, this would require a considerably bigger data sample in order to obtain sensible results. Therefore this approach is suggested for the future research when more data become available.
: The interaction surface (Figure 6 CO2: IDIR plot) illustrates a simultaneous effect of
and
on the expected Z-spread. Interesting to note here that as the percentage of independent directors increases the marginal effect of
on the expected Z-spread declines. Note, that percentage of independent directors varies greatly across different countries; presumably the effect of CO2 emission could also have an un-uniform interstate distribution. Given the size of the data sample used in the current study, this statement cannot be reliably explored. Therefore, this analysis is suggested for the future research when more data become available.
: The interaction surface (Figure 6 INT: CRH plot) illustrates a simultaneous effect of
and
on the expected Z-spread.
![]()
Figure 6. Interaction effects of
terms (
―time to maturity,
―base interest rate,
―level of carbon dioxide emissions to tangible assets ratio,
―dividend health of an issuer, and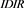 ―percentage of independent directors) on the expected Z-spread.
―percentage of independent directors) on the expected Z-spread.
Noteworthy that the expected Z-spread is maximised when the base interest rate and dividend health of the issuer reach their higher and lower extremes accordingly. Overall we observe that in the economies with high interest rates the improvement in dividend health of the issuer has the strongest negative effect on the expected Z-spread of infrastructure bonds.
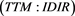 : The interaction surface (Figure 6 TTM: IDIR plot) illustrates a simultaneous effect of
: The interaction surface (Figure 6 TTM: IDIR plot) illustrates a simultaneous effect of  and
and 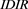 on the expected Z-spread. Noteworthy that
on the expected Z-spread. Noteworthy that 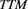 effect varies considerably depending on the percentage of independent directors engaged. Thus a higher percentage of independent directors can be associated with a stronger
effect varies considerably depending on the percentage of independent directors engaged. Thus a higher percentage of independent directors can be associated with a stronger 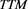 impact on the expected Z-spread.
impact on the expected Z-spread.
Financial risk: s
The dispersion parameter (s) quantifies the degree to which the Z-spread fluctuates in relation to its expected value. It essentially characterises volatility (the tendency of the Z-spread to rise or fall substantially in a short period of time). A bond that is volatile is considered to have a higher risk because its performance may change quickly in either direction at any moment. The model for dispersion parameter (s) is:
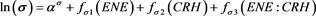
Thus the Z-spread volatility is directly affected by the energy intensity per tangible assets ratio, dividend health of an issuer and interaction of these covariates. The effects can be disintegrated as follows:
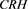 : The dividend health of an issuer has a negative linear effect on the Z-spread volatility (see Figure 7
: The dividend health of an issuer has a negative linear effect on the Z-spread volatility (see Figure 7 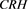 plot) with the marginal effect equal
plot) with the marginal effect equal
to −0.085. This suggests that high dividend health, hence credit standing of the issuer lowers uncertainty around the expected Z-spread of the infrastructure bond.
![]() : The energy intensity per tangible assets ratio has the average main effect on the Z-spread volatility equal to zero (see Figure 7
: The energy intensity per tangible assets ratio has the average main effect on the Z-spread volatility equal to zero (see Figure 7 ![]() plot). However the interaction surface spanned by
plot). However the interaction surface spanned by ![]() and
and ![]() is not flat (see Figure 7
is not flat (see Figure 7 ![]() plot). We observe an inverted u-shaped relationship between
plot). We observe an inverted u-shaped relationship between ![]() and Z-spread volatility for the bond issuer with low dividend health score, on the other hand, the effect between
and Z-spread volatility for the bond issuer with low dividend health score, on the other hand, the effect between ![]() and Z-spread volatility is a u-shaped relationship for the bond issuers with high dividend health score.
and Z-spread volatility is a u-shaped relationship for the bond issuers with high dividend health score.
Financial risk: n,t
The remaining two parameters, namely v and τ control skewness and kurtosis of the Z-spread distortion. In the model selection process none of the covariates when added to v and τ could further improve the likelihood of making the data. As the result models for v and τ are not conditioned on any of the studied covariates and represent intercept-only models. Nevertheless, the estimates for skewness and kurtosis are still useful as indicators highlighting deviation from normality for Z-spread distortion. Thus estimated v parameter equal to −0.13 indicates a negative skewness of the Z-spread distortion (mass of the Z-spread distribution is concentrated on the right) suggesting a larger chance of observing high Z-spreads comparing to what the normal distribution would suggest. The estimated τ parameter equal to 0.43 indicates a considerable leptokurtic shape of the Z-spread distortion with heavy tails (higher probabilities for observing extreme tail Z-spreads than the normal distribution would suggest). Overall there is a substantial amount of skewness and kurtosis in the data that cannot be explained by the selection of covariates, however, these deviations from normality are well captured by the flexible JSU distribution.
Table 2 summarises the effect types and average partial slopes between selected risk factors, expected absolute risk and uncertainty around it. Overall these results show that infrastructure bonds issued by firms with environmental and social risk concerns tend to have higher expected Z-spreads and wider uncertainty around the expectation. Moreover, asymmetric shape of the conditional Z-spread distribution and heavier tails (compared with the normal density function that is usually employed by conventional models) indicate a higher probability of exposure to a large financial risk.
6. Out-of-Sample Model Validation
In order to test the model’s out-of-sample performance we used a quantile-based sampling algorithm to partition the initial dataset into separate training (80% of original sample) and testing datasets (20% of original sample). The test was repeated 10 times and validation results were averaged (training and testing datasets each time were selected randomly). Each test is based on validation algorithm that minimises the global deviance for the training data set and then uses the validation set to calculate the prediction global deviance. This then was used to calculate a prediction error by dividing prediction global deviance over the number of observations in the validation data set.
The average prediction error equals −2.93 (0.88 - standard deviation), while the training error equals −4.45 with (0.25 - standard deviation). Lack of large discrepancies between training and testing prediction errors suggests that the selected model overall has a good out-of-sample performance. This result is benchmarked against a simple linear regression model that assumes a normally distributed response:
![]()
Note that the benchmark model has a considerably higher out-of-sample prediction error, equal 2.28 (5.43 - standard deviation). This highlights the advantage of data-driven non-parametric techniques and use of flexible distributions.
7. Conclusions
This study provides a comprehensive evidence that the issuer related ESR factors have financial risk implications for the infrastructure bond investors. Despite growing attention to environmental and social risk concerns in many industries, there are very few academic outputs (e.g. Lucas and Noordewier [68] , Chen et al. [69] ) that our conclusions can be generalised to. The results of this work extend previous research by identifying the exact ESR related factors (and the type of the relationships) which are associated with the expected finical performance and the balance of risk around the expectation of the global infrastructure projects.
The model developed in this study can provide guidance to policy-makers who might seek to foster or incentivize CO2 emission reduction by firms through the formulation of supporting policies (e.g., tax benefits, subsidies, etc.). Thus, the model can be used in estimating potential financial benefits achieved as the result of the implementation of such policies by firms. Similarly, the model could also provide comparative advantage to financial professionals by better estimating the risk-return probability distribution of infrastructure bonds.
Finally, a few limitations have to be discussed so that they can be addressed in the future research. First of all the type of paradigm employed in this study is a good choice for detecting complex relationships in the data, however, it is not always able to answer the question on why these relationships exist. Secondly, given the narrow specificity of the research question and difficulties in collecting ESR-related information, the studied sample comprises only a small portion of infrastructure bond issuers that disclose their public and social risk related information. This issue could be addressed potentially in the future research when more data are disclosed. To expand upon this research the future study should concentrate on improving the viability of developed model by benchmarking its results against industry insights and alternative modelling methodologies.
*This research was funded by WWF Schweiz, Hohlstrasse 110, 8010 Zürich, Switzerland.