1. Introduction
Studies conducted on seismicity have shown that earthquakes grouping in space and time does not happen randomly, but follows some rules based on interactions between the earthquakes.
The earthquake launching the most energetic seismic activity is known as mainshock, which is caused by the release of previously accumulated energy into the lithospheric volume [1] , while the groups of earthquakes that follow are known as aftershocks.
A shock is considered an aftershock if it happens within the length of the rupture surface that generated the main event, or within a subsidence area (the so-called aftershock area). Besides, it should occur before the seismicity rate of the area goes back to the basic values recorded in the period preceding the mainshock.
However, theory does not always mirror practice. Indeed, it may happen that the area in which the aftershocks occur overlaps with the aftershocks area of another mainshock or with background seismicity.
A mainshock can be followed by two types of aftershocks [2] : 1) Direct aftershocks which are triggered only by a given primary shock and can be adequately described by the Omori law, which starts with the mainshock occurrence; 2) Secondary aftershocks that occur on any faults that have been so strongly stressed by a previous shock that the Omori law starts when the shock is triggered rather than upon the original mainshock occurrence. Secondary aftershocks may be triggered by one of the direct aftershocks or other secondary aftershocks and may significantly consist of earthquakes which are not triggered by original mainshock’s stress changes [2] .
The aftershocks sequences and their spatial and temporal distribution, depend on the mainshock’s characteristics and physical properties as well as the stress, tension, temperature of the occurrence region [3] and are particularly active in the short term (seconds, days), although their activity can go on for years.
The mechanism behind aftershocks triggering is not yet known, but it is conceptually linked to field adjustments from post-mainshock stress [4] , possibly through viscoelastic processes or changes in the pore pressure due to fluids flow [5] ; whatever the actual process is, the aftershocks should be related to mainshock’s rupture plane.
Seismicity studies showed that time-space earthquakes clustering is not a random process, but a proof that the vast majority of them are triggered by the previous ones due to static or dynamic changes in the stress field [6] [7] [8] [9] .
Aftershocks have more defined characteristics compared to any other event in the seismic sequences and are a relaxation process deriving from mainshock dynamic rupture stress [10] .
Aftershocks trend follows the Omori law [10] [11] [12] , which shows an almost hyperbolic curve. The aftershocks’ greatest magnitude event is generally of the order of one magnitude unit lower than the mainshock [13] and the sum of the seismic moments in the entire sequence is usually equal to only about 5% of the mainshock time [14] . The number of aftershocks that occur over a certain period of time following the mainshock is directly proportional to the mainshock’s rupture area [15] .
The aftershock events, usually begin immediately after the mainshock just next to the rupture and around the area affected by the seismic sequence, and are commonly concentrated in places where we might expect Coulomb stress variations resulting from the main rupture [8] , [16] . Often we see them clustered around the rupture point, where the flow rate is lower than co-seismic’s [10] , or along more complex structures inside the rupture [17] . Aftershocks’ spatial distribution seems almost stationary during the sequence, with the mere migrations of the activity observed [18] . However, Mogi [19] observed this phenomenon even for large offshore earthquakes in Japan. Not only the Author noticed a substantial increase in the size of the subsidence zones (aftershock zones) over time but he also discovered that it did not occur in other cases. Aftershocks-affected areas sometimes show a considerable expansion within days or years after the mainshock [19] [20] .
Based on this knowledge, this study has the aim to analyze the seismic sequence and the mainshok-aftershocks relation to define the future development of the aftershock stage.
2. Aftershocks Characteristics and Classification
An aftershock is a smaller earthquake that happens after, and in the same area as, the mainshock. If an aftershock is larger than the mainshock, the event is classified as main, while the previous one is renamed as foreshock. There is no physical distinction in the relaxation mechanism between mainshocks, foreshocks and aftershocks [21] [22] .
In a seismic sequence, the aftershocks form a triggering pattern that starts from the mainshock (source point) which involves determining which are the earthquakes connected directly or indirectly and classifying them not based on the casual link [23] . To make a distinction between mainshocks and aftershocks, in the past several declustering algoritms were proposed [24] - [34] .
Kisslinger [3] qualitatively defines three types of aftershocks: a) Class 1-events occurring in the rupture area of the fault plane or on a thin band around it; b) Class 2-events that occur on the same fault but outside of the co-seismic rupture area c) Class 3-events happening elsewhere, on faults that are different from the one that has generated the mainshock; these events, whether in the same region or not, will not be considered herein as aftershocks, but will be classified as triggered earthquakes. The aftershocks occurring within 24 to 48 hours after a strong earthquake mainly in the co-seismic rupture area, indicate that seismicity is predominantly of Class 1; over longer times the aftershocks area increases [35] [36] [37] [38] [39] , and seismicity is predominantly of Class 2.
By analyzing the various seismic sequences, it was possible to understand how a mainshock may trigger two types of aftershocks (Figure 1 and Figure 2).
![]()
Figure 1. Schematic representation of Nepal earthquake’s aftershocks phase and aftershocks classification. The colored lines indicate the aftershocks cycles.
![]()
Figure 2. Schematic representation of Nepal earthquake’s aftershocks phase and aftershocks classification. The colored lines indicate the aftershocks cycles.
1) Primary or direct aftershocks, which are triggered only by the mainshock (their time of occurrence and magnitude depend on the variations of stress generated by mainshock).
2) Secondary or indirect aftershocks, which are produced by stress variations related to primary aftershocks. They occur after a primary aftershock, and are not directly connected to the original mainshock.
The time elapsed between the first primary aftershock and mainshock may vary, but typically it consists of a few hours/days, while the subsequent secondary ones may happen in different areas and times.
From Figure 1, which shows the scheme of the aftershocks phase’s developmental structure triggered after the Nepal earthquake on 25/04/15 that was obtained by analyzing its branched structure [40] , we can infer that in the seismic sequence a succession of cyclical movements (seismic cycles) was triggered, whose amplitude varies over time and with increasing magnitude and order. Here, any events occur following a specific hierarchisation process where each earthquake can generate other earthquakes [41] .
These seismic events are connected to the event source and are considered as primary [42] . They may also, in turn, generate other minor seismic events, thus triggering a process which continues up to the energy release phase’s triggering point and may end with a major event.
The distribution of the most energetic aftershocks that close the sequence’s seismic cycles is usually repetitive and consists of a first primary aftershock situated in time and space next to the mainshock, followed by a succession of lower magnitude secondary aftershocks and additional primary and secondary aftershocks.
Based on aftershocks time position with respect to mainshock, we obtain the development scheme and classification of the aftershocks shown in Figure 2, where we can observe that big events trigger a seismic events sequence consisting of several primary aftershocks of various order followed by secondary aftershocks of various orders, triggered by the previous ones.
Primary aftershocks may be of various order depending on the branched structure as well as aftershocks sequence’s developmental state. The magnitude values of primary aftershocks tend to grow from the third order onwards.
Figure 3 and Table 1 report the spatial distribution of primary and secondary aftershocks’ seismic sequence that developed after the earthquake occurred in Nepal on 25 April 2015.
We observe that some aftershocks occurred in the co-seismic rupture area while others happened on the same fault, but outside the co-seismic rupture area
![]()
Figure 3. Schematic representation of epicenters of Nepal earthquake occurred on 25 April 2015 and relevant primary and secondary aftershocks.
![]()
Table 1. Primary and secondary aftershocks.
while others, triggered by different earthquakes, occurred elsewhere, on faults adjacent to mainshock’s.
Aftershocks are distributed over a length of 150 km and a width of 70 km, in an easterly direction from the epicenter. One of them, with a 6.6 Mw magnitude (primary second order aftershock) occurred thirty minutes after the mainshock and in the epicentral area. On 12 May, a great Mw 7.3 magnitude aftershock (fourth order aftershock) occurred in the same location as the 25 April mainshock.
This spatial organization, suggests that the seismic rupture initiated on 25 April epicenter spread SE over more than a hundred kilometers, thus showing a SE-oriented stress switching, which probably triggered the 7.3 Mw event that closed the fifth order aftershocks cycle.
Aftershocks’ spatial organization is closely related to any energetic events occured in the aftershocks phase. Immediately after the mainshock, most of the aftershocks are located near or in close proximity to the mainshock’s rupture plane. Then, in many cases, the aftershocks migrate away from the mainshock, at a speed of 1 km/h up to 1 km/year calculated with reference to the mainshock or the first aftershock of first order.
Figure 4 shows the distribution of aftershocks epicenters (USGS data) in the Nepal earthquake over 134 days from the mainshock, where we observe a dis-
![]()
Figure 4. Aftershocks phase in the Nepal earthquake on 25 April 2015. The red stars indicate the mainshock. For a detailed description, see the text.
tribution along the epicenters’ NW-SE direction before the occurrence of the first primary aftershock and an extension in SW-NE direction, with likely involvement of other faults after the first primary aftershock.
In particular, Figure 4(a) shows the SE spread of the aftershocks, from the mainshock to the first aftershock of first order. Figure 4(b) shows the aftershocks epicenters from the first aftershock of first order to the primary second order aftershock, in which we observe a shocks’ SW-NE extension. Figure 4(c), which starts from the first aftershock of first order on 19/11/15, we note a subsequent NE -NW aftershocks’ extension. Figure 4(d) shows the combination in time and space (aftershocks expansion and migration) from mainshock on 19/11/15.
In summary, the chart confirms an aftershocks extension in space and in time which is common to any aftershocks sequences.
The extent of aftershocks’ area extension or migration depends on the position of mainshock and primary most energetic shocks in the aftershocks phase.
Figure 5 and Figure 6 display some reports drafted using 86 primary aftershocks occurred in various areas of the world and recorded by INGV, NIED AND USGS networks between 1970 and 2016.
Figure 5(a) shows the existing relationship between the number of days elapsed between the mainshock and the most energetic primary aftershock and the aftershock magnitude, while Figure 5(b) shows the relation between the dis-
![]()
Figure 5. (a) Relationship between the number of days elapsed between mainshock and the most energetic primary aftershock (abscissa) and the aftershock magnitude (ordinate); (b) Relationship between the distance in kilometers between the mainshock and the most energetic primary aftershock (abscissa) and the aftershock magnitude (ordinate).
![]()
Figure 6. (a) Relationship between the aftershock’s occurrence time from mainshock (abscissa) and the distance between the mainshock (ordinate); (b) Relationship between the mainshock and the most energetic primary aftershock magnitudes.
tance in kilometers between the mainshock and the most energetic primary aftershock and the aftershock magnitude.
In general, our analyses show that in seismic sequences the aftershocks phase tends to develop within seconds, days and years and with a spatial development initially next to the mainshock epicenter, which causes their triggering. Subsequently, they are organized into placed bands at different distances, even of 100 km. The main aftershock’s incidence mostly occurs at a distance of 0 - 50 km.
The frequency of the aftershocks that occur within 24 hours after the mainshock, decreases as the days increase, while aftershocks magnitude values increase as the distance increases.
The percentage of aftershocks that occur within 24 hours after the mainshock is 63%, while for those that occur at less than 50 km is 70%.
Figure 6(a) shows the relationship between the number of days elapsed from the mainshock and the distance between the mainshock and the most energetic primary aftershock. The figure shows that many aftershocks occur less than one day away from mainshock and within 50 km. The aftershocks frequency decreases as both distance (up to hundreds of kilometers) and time (up to approximately 18 days) increase.
Figure 6(b) shows the relationship between the mainshock magnitude and the most energetic primary aftershock, which is valid for any area in the world and can be used to assess an aftershock magnitude.
The average aftershock magnitude value (Mf) is calculated using the following empirical relationship, obtained by the graph displayed in Figure 6(d):
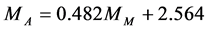 (1)
(1)
3. Methods for Identifying Aftershocks
3.1. Branched Structure
After the occurrence of a strong earthquake, in order to study the future development of the seismic sequence, it is crucial to know how aftershocks develop, in particular the value of their magnitude and their type (primary and secondary). The aftershocks occurrence may indicate a greater seismic hazard of the area in the short time following the mainshock.
A simple and effective method to monitor aftershocks evolution, and to identify the most energetic ones, is based on the seismic sequence time hierarchisation process [40] , where a primary or secondary aftershock of various order can be described by a branched structure originating from the mainshock.
This procedure allows distinguishing the aftershocks directly triggered by the mainshock from those triggered by other second generation higher order shocks.
The method has been tested on various catalogs with good results since aftershocks are easier to define compared to foreshocks.
Figure 7 shows branched structures of various orders that were formed after the Solomon Island earthquake on 21 April 1977 (point source) and primary and secondary aftershocks of various order located at the seismic nodes of branched structures’ branches.
Primary and secondary aftershocks are distinguished by their magnitude-de- pendent position in the aftershocks sequence and by the connections, both direct and indirect, with the mainshock.
Primary aftershocks are triggered by the mainshock, while the secondary, over the time, are triggered by primary aftershocks-induced stress variations.
Thus, a shock could be an aftershock linked either to the mainshock or to one of the previous aftershocks and, at the same time, to the most energetic shock of subsequent aftershocks.
It is apparent that the application of a simple graphic procedure allows isolating the most energetic aftershocks from the rest of the earthquakes and, therefore, even from the background earthquakes, i.e. earthquakes independent of any previous earthquakes.
![]()
Figure 7. Branched structure of Solomon Island earthquake on 21 April 1977.
The aftershocks development’s overall scheme can provide useful information about the future sequence development and the likely occurrence of major events.
3.2. Use of Relative Maximum and Minimum Magnitude Values
The graphic approach proposed is based on mainshock magnitude values and relative maximum and minimum values that are formed during the aftershocks sequence’s time evolution. The graphic procedure allows forecasting the development of the most energetic aftershocks that occur immediately after the mainshock or a primary aftershock and assessing their magnitude.
Figure 8 shows the procedure suited to identify the first relative minimum value that is formed after the mainshock and that allows determining even the beginning of the second seismic cycle in the post-earthquake energy release.
The first step consists in identifying the midpoint (Point 3) of the line joining the mainshock (Point 1) with the minimum value that precedes it (Point 2). From point 2 a horizontal line must be drawn util it intrersects the straight vertical line (Point 4) crossing the most energetic event (Point 1) and this intersection must be joined with the midpoint (Point 3). From point 1 we draw a line parallel to the line crossing points 3 and 4, thus establishing the channel in which magnitude values fluctuations will develop during the first post-earth- quake phase.
Figure 9 shows the procedure suited to detect the most energetic aftershocks directly triggered by the main earthquake or by a primary aftershock and the band in which the magnitude values fluctuations will develop.
From the mid-point we draw an half line crossing the minimum value (Point 1) indicated by the broken line of the relative maximum and minimum values and by the mainshock, then we draw the parallel line whose slope will provide the magnitude value at the first aftershock occurrence point (Point 2).
It is necessary to repeat the same procedure for identifying the position and
![]()
Figure 8. Procedure for determining the first minimum value of the relative maximum and minimum values line. The red star indicates the Nepal earthquake on 25 April 2015, the yellow stars the most energetic aftershocks. The red circles indicate the aftershocks magnitude values in the post-seismic phase.
![]()
Figure 9. Procedure for determining primary and secondary aftershocks. The red star indicates the Nepal earthquake on 25 April 2015, the yellow stars indicate the most energetic aftershocks. The red and blue lines show the aftershocks magnitude values fluctuations range.
the magnitude value of other expected aftershocks (4, 8, 12). It is possibile to implement the same procedure from the most energetic aftershocks and from point M1 to obtain the magnitude values fluctuation range of the aftershock expected. For example, from midpoint A1 it is possible to identify Point 11 using the same procedure and compare it with Point 12 previously identified from point A.
This procedure identifies the channel where future aftershock’ possible fluctuations will occur, when it is formed, after a relative minimum value (Point 5), a temporary relative maximum value (Point 6), also identifying the most energetic one. This method has proved to be very effective, although, from the study of some seismic sequences, we infer that in the energy release phase the values identified through the graphic method are not always respected.
Figure 10 shows the graphic procedure for estimating the expected magnitude values (magnitude target) of primary and secondary aftershocks, depending on the position of relative maximum and minimum values points in respect to the midpoint of the energy accumulation and release phases (seismic cycles), which are triggered in the seismic sequence.
Operationally, for the calculation of an aftershock minimum magnitude target it is sufficient to calculate the value of the midpoint B between the relative minimum M2 and the mainshock. The maximum value is obtained by drawing a line from midpoint M2 up to the calculation point selected (Point B2) and join this with the relative minimum M2 (dashed red line). We then d draw from the mid-point B a line parallel to M2-B2, where the point B3 represents the maximum magnitude value expected. The same procedure can be repeated from midpoint A or from other energetic aftershocks to detect the position of the maximum and minimum magnitude value of other aftershocks expected (Points C2 and C3).
3.3. Index Simplified Force (ISF)
Index Simplified Force ISF is a very simple and sensitive oscillator, which can be
![]()
Figure 10. Procedure for determining the magnitude value of primary and secondary aftershocks.
used to monitor the seismic sequence strength and the relevant development [43] and to control the aftershocks phase.
The ISF overall decay rate is similar to the decay rate of a generic aftershocks sequence.
Moreover, the greater the magnitude of the mainshock the steeper the power decay law (more similar to an exponential decay).
Figure 11 shows the Japan seismic sequence in the time window ranging from 2 January to 31 December 2011, the ISF and simplified Aroon oscillator [40] . Figure 11(a) shows, up to 8 March 2011, an initial portion of small amplitude cyclical fluctuations, followed, on 9 March, by a first peak due to the occurrence of a magnitude 7.3 Mw foreshock (green star) associated with an increase in the number of recorded events and shortly afterwards by a ISF second increase due to the mainshock, whose magnitude was 9.0 Mw (red star), occurred on the same day. A third peak of greater amplitude formed on 13 March with the af-
![]()
Figure 11. (a) Index Simplified Force in the 2011 Japan earthquake’s seismic sequence; (b) Daily seismic sequence. On the right, red-colored Fibonacci levels 0% - 100% are shown.
tershock occurrence, with a magnitude of 6.6 Mw (yellow star) associated with a sharp increase in the number of daily events recorded. After the aftershock on 13 March, the ISF values decreased over time and, at the end of December, reached values similar to pre-foreshock’s on 9 March 2011.
Table 2 reports the most energetic aftershocks closing the seismic cycles that developed in the daily sequence of aftershocks during Japan earthquake in 2011.
Inside the aftershocks sequence we find some seismic levels where magnitude values, during their post-earthquake fluctuation, more frequently stop, which offer some useful information for estimating the magnitude values that might occur in future.
The seismic levels used in this work, which give information on the aftershock sequence’s developmental state are Fibonacci levels [44] .
The levels are 23.6%, 38.2%, 50%, 61.8%, 76.4% and 100%, respectively.
Figure 11(a) and Figure 11(b) show ISF and seismic sequence percentage levels, i.e. the static seismic levels.
The procedure adopted consists in identifying in the seismic sequence or ISF chart the previous maximum (Level A) and minimum value (B) from which the maximum value is derived and then dividing the distance between the minimum and maximum values by carrying Fibonacci percentage levels (green dashed horizontal lines).
The graph thus created provides the following information:
・ The most energetic post-seismic phase usually ends as the magnitude values are set under the seismic level-static of 50%;
・ The highest occurrence frequency of the most energetic aftershocks occurs in the seismic level range between 23.6% and 50%;
・ The occurrence and the magnitude value of the first primary aftershock expected after the mainshock depend on the first minimum level (C) that is formed after the main event. The lower the distance of the seismic level C from maximum value A, the greater the magnitude of the first primary aftershock (usually the subsequent magnitude increase from seismic level C, does not exceed 50% of the magnitude difference between maximum value A and seismic level C);
・ The aftershocks sequence starts at the end of the process, when magnitude values are set under the background seismicity maximum value (D) which usually coincides with seismic levels of 61.8% and 76.4% (with greater frequency), respectively.
![]()
Table 2. Primary aftershocks phase in the Japan earthquake.
To know in advance the magnitude values range of the most energetic aftershocks sequence, it is possible to use a quite simple and fast graphic method, which consists in building a dynamic seismic level by combining the maximum value (main event) with the end of the 14.6% seismic level selected for the calculation (Point E1). From the left end of the 23.6% seismic level we draw a parallel line to the previously plotted dynamic level in order to identify Point E2.
The range between the dynamic seismic levels’ ends (Points E1 and E2) represents the preliminary range of magnitude values of higher order most energetic aftershocks.
Figure 12 shows the relationship between the number of daily events and ISF (all values were considered positive) and between the daily magnitude (maximum value recorded during the day) of aftershocks and IFS.
The graph displayed in Figure 12(a) was built by plotting the highest ISF value (point A) which usually coincides with the day of the mainshock or a subsequent more energetic aftershock, and joining this point with the origin of the axes (0,0). Subsequent ISF values are progressively arranged along this segment from Point A to the origin of the axes.
The segment represents a trend line expressing the temporal behavior of the aftershocks sequence through ISF.
The ISF chart seems to follow a linear pattern that allows predicting the aftershocks phase evolution and end. In fact, when the ISF values begin to cluster near the axes’ origins, it means that the aftershocks phase is about to be completed. In the graph shown in Figure 12(b), the IFS features a logarithm trend with very dispersed values around the average value, representing a source of uncertainty in the relationship between the daily maximum magnitude and ISF.
Figure 13 shows some reports that can provide useful information on aftershock sequence development.
Figure 13(a) and Figure 13(b) shows the time trends in the number of daily
![]()
Figure 12. (a) Relationship between daily number of earthquakes and ISF. The black line is the interpolating line, while the red line is the trend line of the aftershocks sequence provided. The green circle shows the greatest ISF value; (b) Relationship between the daily maximum magnitude and ISF.
![]()
Figure 13. (a) Relationship between the progressive number of days and the number of daily events; (b) Relationship between the progressive number of days and magnitude values; (c) Relationship between the progressive number of days and ISF; (d) Relationship between the progressive number of events and ISF in energy accumulation and release phases. The green and red circles indicate the greatest ISF value in the energy accumulation and release phases.
events and magnitude values, while Figure 13(c) displays the ISF temporal trend. The latter figure shows that an exponential decay prevails in the very short term, while a linear ISF decay is dominant in the long term.
Figure 13(d) reports the relationship between the number of daily events and ISF values in relation to energy accumulation and release phases. By default, we assumed that the energy accumulation earthquakes have a lower magnitude value compared to the previous one, while if the magnitude value is greater than the previous earthquake, they are considered as release energy earthquakes.
The energy accumulation and release phases originating from ISF maximum values show that energy accumulation shocks outnumbered the energy release phase’s and that the energy accumulation phase was stronger shortly after the mainshock (ISF values are greater and closer to the point of origin (B).
This graph allows evaluating the aftershocks phase development and estimating systematically the ISF value through the following relation:
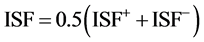 (2)
(2)
where,
ISF* is the index of the energy release phase strength (ISF > 0).
ISF− is the index of the energy accumulation phase strength (ISF < 0).
The ISF+ and ISF− values can be obtained from the ISF decay curves displayed in Figure 13(c) or from Figure 13(d).
Besides, in order to predict when the most energetic energy release phase will end, Figure 13(d) shows a simple graphic procedure based on the energy accumulation phase’s IFS-value. The procedure is as follows: on the positive ordinate axis the ISF maximum value related to the energy accumulation phase is reported (Point C). From this, a line is plotted (dashed red line) in parallel with the line joining the origin with Point B. Intersection point D between this parallel line and the line joining the origin with the point A, separates the phase in which the most energetic aftershocks occur (IFS+ values greater than D) from the least energetic one (IFS+ values smaller than D).
Figure 14 shows the relationship between the number of daily events and ISF in relation to some earthquakes occurred in Italy, Gulf of Alaska, Sumatra and Japan.
![]()
Figure 14. Relationship between the number of daily events and ISF of the following earthquakes: (a) Gulf of Alaska of 30/11/1987; (b) Sumatra on 26/12/2004; (c) Japan 11/03/2011; (d) L’Aquila 06/04/2009; (e) Emilia 20/05/2012; (f) Central Italy, 30/10/2016.
The aftershocks phase can be monitored through the branched structure as well.
Figure 15 presents ISF hierarchisation process in relation to four primary values of various orders. Simplified Aroon oscillator allows monitoring the trend and identifying the warning signs that precede the highest ISF values.
Usually the first primary point of first order closes the most energetic post-seismic phase, while the closure of the most energetic aftershocks starts from the primary point of higher order with the greatest frequency.
3.4. Numerical Method to Calculate Aftershock’s Magnitude
Knowing the magnitude value of the most energetic aftershock that follows a mainshock is crucial to study the sequence’s time evolution and obtain information on possible major earthquakes in the future.
The empirical Båth law [45] states that the average difference in magnitude between a mainshock and the most energetic aftershock is 1.2 (Δm), independently of the mainshock magnitude.
Subsequent studies have confirmed the Båth’s law statement, but have provided Δm values in the 0 - 3 range [2] [46] .
Figure 16 shows the empirical relations valid for any area in the world that allow us to estimate an aftershock magnitude knowing mainshock or aftershocks’ previously occurred.
The report shown in Figure 16(a) was obtained from the study of primary
![]()
Figure 15. ISF hierarchisation. Under the ISF chart is the simplified Aroon oscillator.
![]()
Figure 16. Relationship between mainshock and the most energetic aftershocks.
and secondary aftershocks whose order was greater than M > 3.6, recorded by INGV, NIED AND USGS seismic networks between 1970 and 2016.
![]() (3)
(3)
where MM is the magnitude value of the mainshock or of a subsequent, more energetic aftershock.
The empirical report points out that an aftershock magnitude is, on average, 0.484 (Δm) smaller than the mainshock or aftershock which it depends on and suggests a certain degree of self-similarity to the earthquake that has triggered it.
Figure 16(b) shows the relationship between the mainshock magnitude and the most energetic aftershock’s recorded within ten days after the mainshock occurrence and in an area of 50 km around the mainshock epicenter.
The aftershock average magnitude value (MA) is calculated by the following relation obtained from the analysis of 55 strong earthquakes occurred in various areas of the world:
![]() (4)
(4)
The average difference in size between the mainshock and the most energetic aftershock is 1.287 (Δm), which is slightly higher than that obtained by the empirical Båth’s law.
Figure 17 shows the relationship between the mainshock magnitude and the most energetic aftershock’s recorded within twenty-four hours after the mainshock.
The aftershock average magnitude value (MA) is estimated by the following relation obtained from the analysis of 128 strong earthquakes occurred in various areas of the world:
![]() (5)
(5)
The average difference in size between the mainshock and the most energetic aftershock is 1.575 (Δm).
4. Conclusions
Any mainshock is generally followed by a series of aftershocks, whose duration
![]()
Figure 17. Relationship between the most energetic mainshocks and aftershocks.
may vary from a few weeks to several months or years.
Aftershocks typically give birth to a series of primary and secondary aftershocks of different orders whose magnitude is lower compared to the main event’s, which can be identified through a sequence hierarchisation process. The primary aftershocks result from a triggering process due to mainshock-induced stress variation, and the secondary aftershocks are triggered by stress changes occurred in primary aftershocks.
During our analyses:
・ we have created an empirical relation valid for any area in the world, to estimate an aftershock’s magnitude knowing that of a mainshock or a previous aftershock;
・ we have observed that some aftershocks occur along the same fault that has generated the mainshock, or outside the area where the seismic sequence develops and additional aftershocks can occur on adjacent faults;
・ based on a graphic procedure applied using the seismic sequence’s relative maximum and minimum values, we obtained useful information for predicting the most energetic aftershocks and assessing their magnitude;
・ we suggested the use of the index simplified force-ISF in combination with Fibonacci levels, which allows predicting an aftershocks sequence’s time evolution and then the developmental state reached by the seismic sequence;
・ we determined the relationship between the mainshock’s magnitude and the most energetic aftershock’s recorded within ten days of the mainshock occurrence and within an area of 50 km around the mainshock epicenter;
・ between the mainshock’s magnitude and the most energetic aftershock’s recorded within twenty-four hours after the mainshock, we have provided an average magnitude difference of 1.287 and 1.575, respectively, which is slightly higher than that obtained with the empirical Båth’s law.
This method allows us to monitor an aftershock development in the short- medium term, providing useful insights into its future development. As some of the aforementioned procedures show no close mainshock-aftershock relations, we believe that they deserve further in-depth investigations in order to obtain an even more effective forecasting model.