1. Introduction
The neutrinos are neutral fundamental particles, which now seems mysterious because of their extremely weak interaction with matter. The elucidation of the causes of this mystery is a most important objective of this field of physics.
W. Pauli was the first who proposed the idea of the existence of neutrinos. He suggested the possibility of their existence in an effort to save the law of conservation of energy in 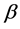 -decay.
-decay.
Further detailed study of 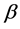 -decays gave the first experimental evidence of neutrino’s possible existence. However, in order to speak with confidence about the existence of neutrinos, it was necessary to detect neutrinos in a free state at some distance from the place of their birth.
-decays gave the first experimental evidence of neutrino’s possible existence. However, in order to speak with confidence about the existence of neutrinos, it was necessary to detect neutrinos in a free state at some distance from the place of their birth.
For the first time it was made by F. Reines and C. Cowan in the experiment, where the nuclear reactor served as the source of neutrinos. They firstly determined that the value of cross section of the antineutrino capture was very small.
Further studies of nuclear reactions that took place with the participation of neutrinos have shown that neutrinos existed in two different modifications: neutrino and antineutrino.
The conclusion about the existence of muonic neutrinos and electronic neutrinos was made by L. Ledermanom and his colleagues on the basis of results of their experiment (Figure 1). In this experiment, a beam of protons with energy of 15 GeV, was aimed at a beryllium target, which was a source of 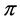 - mesons.
- mesons.
The decay of 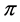 -mesons gave a beam of
-mesons gave a beam of 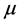 -mesons and neutrinos. The detector was protected from all particles by a powerful iron shield. Only neutrinos could pass through it to cause reactions:
-mesons and neutrinos. The detector was protected from all particles by a powerful iron shield. Only neutrinos could pass through it to cause reactions:
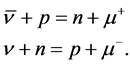 (1)
(1)
Wherein, the electronic modes of these reactions in Lederman’s experiment
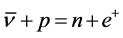 (2)
(2)
 (3)
(3)
have not been detected.
On the basis of this experiment, it was concluded that neutrinos, if they were formed at the birth of muons, carried some muonic “charge”, so they could participate in the future reactions of the birth of exclusive muons.
2. Photons and Neutrinos
There is another particle in nature-the photon, which has some common features with the neutrino. Neutrinos and photons are stable particles that move in space with the speed of light. Neutrinos, the same as photons have no electrical charge and mass.
Let us consider the properties of photons, that form an electromagnetic wave.
![]()
Figure 1. Schematic representation of the Lederman’s experimental setup, where p is the beam of protons with 15 GeV energy; Be is the beryllium target; D is the spark camera; Fe is the protection made of iron.
Plane polarized electromagnetic waves in vacuum have two orthogonal components. Electric field oscillates in a plane perpendicular to the propagation vector. If the source of the electromagnetic wave is a magnetic dipole![]() , then the oscillation amplitude of the electric field away from it will be [1] [2] :
, then the oscillation amplitude of the electric field away from it will be [1] [2] :
![]() (4)
(4)
The magnetic field oscillates in plane perpendicular to the electric field and the direction of propagation:
![]() (5)
(5)
We can see from these formulas that the amplitude of oscillations of the electric field in the wave depends on the second time derivative of the function describing the oscillating dipole only.
At the same time the oscillation amplitude of the magnetic field depends also on the first time derivative. This contribution is ![]() times less than the contribution from the second derivative and it can be ignored.
times less than the contribution from the second derivative and it can be ignored.
However, it becomes important, if![]() . In this case, the wave will be deprived from the electric component. Only magnetic wave with the intensity proportional to
. In this case, the wave will be deprived from the electric component. Only magnetic wave with the intensity proportional to![]() , will propagate in space.
, will propagate in space.
If photon with both magnetic and electric components is circularly polarized, its spin equals to![]() . It seems natural to assume that a circularly polarized magnetic photon devoid of electric component should have spin equal to
. It seems natural to assume that a circularly polarized magnetic photon devoid of electric component should have spin equal to![]() .
.
Another unusual feature which a magnetic photon should have arises from the absence of magnetic monopoles in nature.
Conventional photons with an electrical component dispersed and absorbed in substances mainly due to the presence of electrons.
In the absence of magnetic monopoles a magnetic photon must interact extremely faintly with matter and the length of its free path in the medium should be about two dozen orders of magnitude greater than that for conventional photon [2] .
However, it should be emphasized that the periodically oscillating magnetic dipole (as electric dipole too) always excites the electromagnetic wave with an electric component.
Therefore, at any circumstances, an oscillating dipole can not radiate a purely magnetic photon.
3. How Magnetic Photon Can Be Excited?
3.1. The Heaviside’s Function and Its Derivatives
Alternatively, a quickly emerging magnetic moment must excite oscillations in the ether.
This phenomenon occurs, for example, in the chain of successive trans- formations of ![]() -meson
-meson ![]() -meson
-meson ![]() electron (Figure 2).
electron (Figure 2).
![]() -meson has no magnetic moment, but
-meson has no magnetic moment, but ![]() -meson has it.
-meson has it.
![]()
Figure 2. Schematic representation of the transfor- mations chain of ![]() -meson in
-meson in ![]() -meson and finally into electron. Below: the resulting magnetic moments are shown schematically.
-meson and finally into electron. Below: the resulting magnetic moments are shown schematically.
The transformation of ![]() -meson into
-meson into ![]() -meson occurs in a very short time. The evaluation of this time can be obtained using the uncertainty relation:
-meson occurs in a very short time. The evaluation of this time can be obtained using the uncertainty relation:
![]() (6)
(6)
A little less time required for the conversion of ![]() -meson into electron.
-meson into electron.
The sudden appearance of the magnetic moment at these conversions can be described by the Heaviside function.
The Heaviside’s stair function equals to zero for negative argument and 1 for positive one. At zero, this function requires further definition. Usually, it considered to be convenient, at zero to set it equal to 1/2:
![]() (7)
(7)
The first derivative of the Heaviside’s function ![]() is the Dirac
is the Dirac
![]() -function:
-function:
![]() (8)
(8)
Wherein, the second derivative of Heaviside’s function is absent (Figure 3).
3.2. Neutrinos and Antineutrinos
The magnetic dipole moment occurs very quickly at the ![]() -decay.
-decay.
In accordance with the electromagnetic model of neutron, the generalized momentum (spin) of relativistic electron is equal to zero if it forms a neutron [3] . Thus the magnetic moment of electron becomes unobservable. At the ![]() -decay of a neutron, an electron acquires freedom, and with it a spin and magnetic moment. For the emitted electron with a speed close to the speed of light, this
-decay of a neutron, an electron acquires freedom, and with it a spin and magnetic moment. For the emitted electron with a speed close to the speed of light, this
![]()
Figure 3. The Heaviside’s function and its first derivative. The second derivative of this function is absent.
process should take place as leap.
Experiments show that the ![]() -decay of neutron is accompanied by the emission of antineutrino:
-decay of neutron is accompanied by the emission of antineutrino:
![]() (9)
(9)
Thus, ![]() -shaped surge magnetic field arising after a sudden onset of magnetic moment of electron can be identified as an antineutrino.
-shaped surge magnetic field arising after a sudden onset of magnetic moment of electron can be identified as an antineutrino.
Another implementation of magnetic ![]() -quantum should arise at the reverse process that is at the K-capture. In this process, electron initially forms an atom shell and has its own magnetic moment and spin. At a certain moment it is captured by nucleus and forms neutron together with proton.
-quantum should arise at the reverse process that is at the K-capture. In this process, electron initially forms an atom shell and has its own magnetic moment and spin. At a certain moment it is captured by nucleus and forms neutron together with proton.
This process can be described by the inverse Heaviside function. This function is equal to 1 at negative times and reset at![]() :
:
![]() (10)
(10)
In this process should occur magnetic ![]() -quantum with reverse orientation of the field relative to its propagation vector
-quantum with reverse orientation of the field relative to its propagation vector ![]() (Figure 4).
(Figure 4).
Such “reverse” surge corresponds to the neutrino in the K-capture reaction:
![]() (11)
(11)
4. Mesons as Excited States of Electron
The chain of transformations of ![]() -meson
-meson ![]()
![]() -meson
-meson ![]() electron gives birth to three neutrinos (Figure 2).
electron gives birth to three neutrinos (Figure 2).
No other products besides neutrino and antineutrino do occur in these reactions. That leads us to an assumption that the pion and muon should be the excited states of electron.
These mesons have masses
![]()
Figure 4. Two Heaviside’s stairs that are responsible for the birth of neutrino and antineutrino.
![]() (12)
(12)
Let us assume that the excited state of the electron is formed from a particle
with mass ![]() (where
(where![]() ) and charge e rotating in a circle of
) and charge e rotating in a circle of
radius R with the velocity![]() .
.
We assume that the excited states are stable if their de Broglie wavelengths are integer times of their circumferences
![]() (13)
(13)
where ![]() is length of de-Broglie wave,
is length of de-Broglie wave,
![]() is integer.
is integer.
Invariant angular momentum (spin) of such particles
![]() (14)
(14)
where ![]() is vector potential of the magnetic field generated by the
is vector potential of the magnetic field generated by the
rotating charge.
The rotating charge e creates magnetic moment
![]() (15)
(15)
and we get
![]() (16)
(16)
where ![]() is the fine structure constant.
is the fine structure constant.
According to Equation (16) at the condition![]() , the relativistic factor
, the relativistic factor
![]() is equal to
is equal to![]() . Wherein, the mass of the particle is
. Wherein, the mass of the particle is
![]() (17)
(17)
This value of mass is very close to the mass of ![]() -meson (12), which has a spin equal to zero:
-meson (12), which has a spin equal to zero:
![]() (18)
(18)
At spin![]() , the relativistic coefficient
, the relativistic coefficient ![]() equal to
equal to ![]() (at n =
(at n =
2) and mass of particle
![]() (19)
(19)
This value of mass is very close to the mass of ![]() meson (12) which has spin =
meson (12) which has spin =![]() :
:
![]() (20)
(20)
5. About Muonic Neutrino
5.1. Types of Neutrinos
The reactions of antineutrino and neutrino with nucleons have muonic and electronic modes:
![]() (21)
(21)
![]() (22)
(22)
The Lederman’s experiment has shown that those neutrinos that were born in the transformation pion ![]() muon can participate only in muonic modes of reactions in the future.
muon can participate only in muonic modes of reactions in the future.
While electronic modes are not implemented at all.
This result is surprising.
All neutrinos―muonic and electronic―are born with the abrupt appearance of magnetic moments. The Heaviside’s functions describing this process have only one variable. The stair has two meanings only: up or down. This is in according with existence of neutrinos or antineutrinos (Figure 4). Heaviside’s stairs can not have any other parameters. It is impossible to put any label for them. Magnetic gamma-quanta can not bear any specific muonic and electronic “charges”.
This seems quite unnecessary to assume that the birth of a free electron in the ground state and the birth of it in the excited state (as muon) must be described in different Heaviside’s stairs.
Differences may be in the magnitude of these stairs. But because of a wide range of energies characteristic for neutrinos at ![]() -decay, this parameter can not distinguish the types of neutrinos.
-decay, this parameter can not distinguish the types of neutrinos.
5.2. The Lederman’s Experiment
The primary beam of protons with energy of 15 GeV was used in the L. Lederman’s experiment [4] . As a result of their interaction with the target, a beam of highly energetic charged ![]() -mesons was formed. In turn at their decay, highly energetic charged
-mesons was formed. In turn at their decay, highly energetic charged ![]() -mesons and neutrinos were created.
-mesons and neutrinos were created.
In future, the muonic reaction mode was observed only and e-mode reaction was not registered.
On this basis, it was concluded on the existence of specific muon-type neutrinos. This conclusion would be true if these reactions would be equally probable. However, this is not the case, since products of these reactions have different phase volumes.
For example, let’s turn our attention on the reaction of the charged ![]() -meson decay. This decay has two modes:
-meson decay. This decay has two modes:
![]() (23)
(23)
Measurements show that the muonic mode of this reaction is more probable for ![]() times.
times.
The reason of the electronic channel suppression is that these reactions generate relativistic electrons.
Because of the kinetic energy of electrons in this decay much more of their mass and their helicity is preserved with good accuracy, this mode of decay must be suppressed relatively to the muon mode on the factor [5]
![]() (24)
(24)
In the reaction of interaction of neutrinos with nucleons Equation (21) - Equation (22), we should expect the same phenomenon, because there are muonic and electronic modes of reaction also, and electronic mode must be suppressed because of its relativism.
At time when L. Lederman with his colleagues made their measurements, this was not known and this factor can not be taken into account.
For this reason we can assume, that L. Lederman and his colleagues found no electrons and positrons not because neutrinos had a specific muon “charge” but due to the strong suppression of the electron channel of reaction.
5.3. How to Clarify the Lederman’s Experiment?
The primary proton beam used Lederman had very high energy. This helped him to form a large beam of neutrinos flying forward. However, this advantage led to the suppression of the electronic mode of reaction.
To avoid this one needs to repeat the Lederman’s experiment at lower energy of primary protons.
Born ![]() -mesons will have lower kinetic energy if energy of protons in the primary beam is only slightly above the threshold of their birth in the pp reaction (290 MeV). Neutrinos, born as a result of
-mesons will have lower kinetic energy if energy of protons in the primary beam is only slightly above the threshold of their birth in the pp reaction (290 MeV). Neutrinos, born as a result of ![]() -meson decay will have energy of about 30 MeV. The interaction of these neutrinos with nucleons of the target can not give the muonic branch of reaction because the threshold of muon birth is about 105 MeV. Whereas the electron branch of reaction should go with a standard cross section.
-meson decay will have energy of about 30 MeV. The interaction of these neutrinos with nucleons of the target can not give the muonic branch of reaction because the threshold of muon birth is about 105 MeV. Whereas the electron branch of reaction should go with a standard cross section.
However, it should be noted that the registration of the electron mode in this case is complicated by the fact that the decay of ![]() -meson will take place in
-meson will take place in ![]() -angle.
-angle.
To improve the geometry of this experiment one can raise energy of primary protons to about 360 MeV. At that the threshold of muon birth would not yet been achieved, but the registration of the electron mode should increase by several times due to more favorable flux of neutrinos.
It is important that if we increase the energy of the proton primary beam just about only 10 MeV, produced neutrinos will be able to induce the muonic mode of reaction and e-mode in this case must be suppressed.
6. Neutrinos and ![]() -Decay
-Decay
According to the electromagnetic model, neutron is a corpuscle in which relativistic electron revolves around proton [2] [3] [6] .
In this description of neutron, one can seen a lot in common with the model of Bohr hydrogen atom. The difference is that the electron shell of Bohr atom is formed by non-relativistic electron, and in case of neutron, it is relativistic.
The electromagnetic model makes it possible to predict with high accuracy almost all properties of neutron.
Thus we can calculate the neutron mass, its magnetic moment, the energy of its decay. In addition, this model allows us to explain the nature of nuclear forces. At least calculated values of binding energy of light nuclei based on this model are in a good agreement with measured data [2] [6] .
However, this model can not predict the lifetime of neutron.
In the electromagnetic model, there are no apparent reasons, that can cause the reaction of neutron decay
![]() (25)
(25)
It should be noted that the Bohr atom itself also can not decay into proton and electron. This requires an external impact.
Now we can assume that the decay of the neutron equilibrium state requires external influence too.
In a searching of the neutron decay cause we should pay attention to the existence of the known and experimentally studied reaction of neutron inter- actions with neutrinos (3).
Given its existence, we can assume that the neutron decay can occur as a result of exposure to the neutrino flux penetrating our earthly laboratories. The reaction of energetic neutrinos scattering can lead to dissociation of a neutron:
![]() (26)
(26)
Currently, there are measurements, suggesting the possible influence of the flux of reactor neutrinos on ![]() -decay.
-decay.
Measurement of the neutron lifetime in the last century were carried out on reactors of relatively low power. The average result of these measurements has been reduced to the lifetime ![]() (Figure 5).
(Figure 5).
In 2004, these measurements were taken on the powerful research reactor in Grenoble [7] . These measurements gave the value of the neutron lifetime![]() . This value on 6 standard errors differs from the equally
. This value on 6 standard errors differs from the equally
![]()
Figure 5. The results of the neutron lifetime measurement. The measurement of 2004 was held on the powerful Grenoble reactor with high neutrino flux.
accurate measurements carried out earlier on reactors with less power. The explanation for this fact is currently not found.
It can be assumed that the observed difference may be possible arose due to neutrino flux of the powerful reactor.
7. Conclusions
Thus, the concept of magnetic ![]() -quanta allows us to understand all main features of neutrinos:
-quanta allows us to understand all main features of neutrinos:
-neutrinos almost never interact with matter because magnetic monopoles do not exist;
-spin of neutrino is equal to ![]() as they have no the electrical component;
as they have no the electrical component;
-neutrinos arise in ![]() -decay as the magnetic moment occurs at the same;
-decay as the magnetic moment occurs at the same;
-there are two types of neutrinos because there are two types of stairs.
And also, it allows us to consider ![]() -meson and
-meson and ![]() -meson as excited states of electron and to predict their masses with good accuracy.
-meson as excited states of electron and to predict their masses with good accuracy.