How to Identify Foreshocks in Seismic Sequences to Predict Strong Earthquakes ()
1. Introduction
From the observation of several seismic sequences, we infer that some earthquakes are preceded by events of increasing magnitude related to the main shock, which are called foreshocks [1] .
Several studies conducted on seismic sequences show how the seismicity increased significantly before the mainshock. For example, 10 days before the 2009 L’Aquila mainshock occurred, the foreshock sequence was concentrated in the hanging-wall domain of the normal Paganica fault [2] .
The foreshocks are one of the few well-documented precursors to large earthquakes: Therefore, understanding their very nature is crucial for earthquake prediction and hazard mitigation. Several studies use foreshock sequences with (combined with) a statistical and probabilistic approach [2] to predict earthquakes (retrospectively) [3] .
We believe that foreshocks are the manifestation of an ongoing energy release process, with different spatial and temporal scales, which leads to the mainshock. During its manifestation time, the seismic sequence analysis may be an appropriate tool to highlight the various stages of preparing a strong event. Under this approach we have noticed that an area seismicity before major earthquakes shows a certain organization [2] , according to a repetitive developmental pattern of “Progressive Earthquakes”-type, [1] consisting of a succession of one or more foreshocks of various order and one or more mainshocks.
The analysis performed suggests that the space-time occurrence of foreshocks, ranges from a few hours up to years before the mainshock, and from a few kilometers to thousands of kilometers from mainshock. It is in fact believed that foreshocks may also occur in areas relatively far from the mainshocks and be part of an external energy release process, which influences the area by triggering the main event [4] .
For a better understanding of foreshocks temporal organization during the energy release phase, we propose some simple graphical and numeric procedures that can be used for the preliminary forecast of a major event.
2. Foreshocks’ Characteristics
Foreshock sequences are the most obvious precursor to large earthquakes: therefore, understanding their origin and relation to mainshocks is crucial for earthquake prediction and hazard mitigation. Previous studies conducted on immediate foreshocks in California suggest that these events may be part of a mainshock rupture nucleation process, because estimated Coulomb stress changes from foreshocks are too small to produce stress triggering and observed foreshock areas scale with mainshock magnitude, are consistent with nucleation instead of earthquake-to-earthquake triggering [2] [5] [6]
Foreshocks occur close to the mainshock and most likely are part of the nucleation process [7] . They may be both physical and tectonic. Most short- and impending-term foreshocks that occur close to major shocks are considered as physical. In general, foreshocks occurring around the epicentral area can be considered as tectonic precursors, as they result from occasional plates’ shifting or blocks shifting along the fault plane that will break [8] . They most frequently occur in areas featuring moderately heterogeneous rocks [9] and in the presence of a moderate pre-stress and rupture stress [10] .
Foreshocks’ magnitude values and position during the energy realease phase allow the implementation of useful models for predicting a strong earthquake. However, it is necessary to know the features that distinguish them from other earthquakes. Through the graphical analysis of the seismic sequence, it is possible to highlight the foreshocks’ characteristics and their grouping in various orders, based on magnitude and period.
Defined as the “foreshocks’ height”, magnitude represents the distance, in terms of energy, between a minimum and the subsequent maximum, while period is the time or the number of shocks between a foreshock and the next.
Depending on the period or the number of shocks between a foreshock and the next within the seismic sequence, it is possible to identify foreshocks of different magnitude orders. First order foreshocks characterize short-medium term time windows, while those of second order usually occur immediately before the mainshock and exactly in the same area where the mainshock occurs.
The time elapsing between the last second order foreshock and the mainshock may vary but it typically consists of few days, while those of first order may happen in different times and areas.
Based on foreshocks magnitude values and temporal position, which characterize the energy release phase, we obtain the following “Progressive Earthquakes”-type developmental patterns [1] :
a) From one or more first order or short to medium-term foreshocks and mainshock (Figure 1(a));
b) From one second order or impending-term foreshock and mainshock (Figure 1(b));
c) From one or more first order or short to medium-term foreshocks, one second order or impending-term foreshock and mainshock (Figure 1(c));
d) From one or more various orders foreshocks and from multiple mainshocks (Figure 1(d)).
By observing the graphs shown in Figure 1, we understand how each earthquake is followed by a energy accumulation (red segment) and by an energy re-
![]()
Figure 1. Schematic representation of Progressive Earthquakes patterns [1] . The green and red lines respectively show the energy release and accumulation phases. The green star indicates the foreshock, the yellow star the aftershock, while the red star shows the mainshock.
lease phase (green segment) triggered by small magnitude shocks. Major events, complementing the “Progressive Earthquakes” pattern, in turn trigger a long- term energy accumulation phase that consists of two or more energetic aftershocks.
Figure 2 and Figure 3 show the magnitude values trend and different order foreshocks position in relation to the monthly long-term seismic sequence’s mainshock in Japan and to the short-term one preceding the earthquake occurred in L’Aquila on 6 April 2009.
By observing the graph of the Japanese seismic sequence we can notice two “Progressive Earthquakes”-type patterns consisting of two first-order foreshocks and one mainshock, in which the temporal distance between the second foreshock and the mainshock is greater compared to that between the first and the second foreshock, while the magnitude values decrease.
In the graph showing the seismic sequence of L’Aquila, we see that the energy release pattern consists of three first order foreshocks, two second order foreshocks and one mainshock. The three first-order foreshocks show an “additive/constant” model (green line) in which the foreshocks’ magnitude values show a proportionality relationships as the number of seismic events increases, while the second order foreshocks and the mainshock, show a multiplicative/amplified model (red line) where the magnitude values between the foreshocks and mainshock amplify as the number of seismic events raises. This amplified effect is due to the short-term occurrence between foreshocks and the mainshock, which usually lasts just a few days.
Figure 4(a) and Figure 4(b) show the relationship between the foreshock magnitude and the number of days elapsed since the mainshock, processed using earthquakes in the “Progressive Earthquakes”-type energy release pattern con-
![]()
Figure 2. Earthquake in Japan on 3 March 2011. Green stars show mid-term foreshocks (first order) while red stars indicate the mainshocks. The vertical axis shows the magnitude values, while the horizontal axis displays the progressive number of months recorded in the period analyzed.
![]()
Figure 3. Earthquake in L’Aquila on 6 April 2009. Green stars show short-term foreshocks (first order), green squares indicate impending-term foreshocks (second order), while red show the mainshock. The vertical axis shows the magnitude values, while the horizontal axis displays the progressive number of events recorded in the period analyzed.
![]()
Figure 4. Relationship between foreshock magnitude (y-axis) and the number of days elapsed between foreshock and mainshock (x-axis): (a) related to the whole world; (b) related to Italy.
cerning 128 earthquakes occurred in various areas of the world and in Italy.
Figure 5(a) shows the relationship between the distance between the foreshock epicenter and the mainshock’s and the number of days elapsed between foreshock and mainshock, while Figure 5(b) shows the relationship between the foreshock magnitude and the distance between the foreshock and mainshock epicenters.
The graphs and Table 1 display the following significant trends related to foreshocks frequency rate and characteristics:
1) Many earthquakes occur less than thirty days after the last foreshock, but quite a number of foreshocks occurs twenty-four hours before the mainshock;
2) The frequency rate of foreshocks occurring within a radius of 50 km and over thirty days, decreases as distance and time increase;
3) Closer events in time and space, show higher magnitude;
4) Magnitude values decrease as distance and number of days increase.
The results obtained show that in some seismic sequences, the “Progressive Earthquakes”-type energy release phase tend to develop near the epicenter of the main shock.
![]()
Figure 5. (a) Relationship between the number of days elapsed between foreshock and mainshock (x-axis) and the distance between the foreshock and mainshock epicenters (y-axis); (b) the relationship between the distance between the foreshock and mainshock epicenters (x-axis) and the magnitude of the foreshock (y-axis).
![]()
Table 1. Correlations between foreshocks and earthquakes.
3. Foreshocks-Identifying Method
3.1. Use of Trendlines
Today it is believed that a foreshock is physically indistinguishable from any other earthquake, until a subsequent mainshock classifies it as such [11] [12] [13] .
The methodology proposed to identify foreshocks is based on identifying the dynamic trendline that characterize the development of the energy accumulation and release phases [1] .
As we can infer from Figure 6, to highlight the energy accumulation and release phases multiple points of relative maximum both in the case of increasing (points 1, 2, 3) and decreasing (points 4, 5, 6) magnitude values, have been joined with a straight line.
As their numerical value varies over time, these straight lines are called dynamic trendlines. Trendlines clearly show the direction the magnitude values are moving in both in the impending and long-term and until the trend remains unchanged.
A seismic events’s trend is considered unchanged as long as there are no clear signs of reversal, such as the trendline break. In fact, the crossing of the energy accumulation trendline (transition point) marks the beginning of an energy release phase that can be of “Flash earthquakes-” or “Progressive Earstquakes-” type [1] . The first is characterised by one or more mainshocks, the second by an initial foreshock followed by a first magnitude values’ fall, which means that the magnitudo values are returning close or under the energy accumulation phase’s trendline. Subsequently, the magnitude values begin to raise again up to form a second foreshock from which it is possible to obtain the direction of the energy release phase’s trendline.
Besides showing the ongoing trend, it seems that the trendlines momentarily prevent the magnitude values from raising and, in some cases, they allow knowing in advance certain levels of magnitude that will be achieved in the future. In fact, the Figure 6 shows also how the knowledge of the magnitude levels achieved in points 1 and 2 allows calculating in advance the magnitude value of point 3 in the energy accumulation phase or of point 6 in the energy release phase after points 4 and 5 have formed.
The trendline drawn from points 6 (first order foreshock) and 7 (aftershock) allows identifying the second order foreshocks 8 and 9.
An earthquake in the “Progressive Earthquakes”-type energy release pattern cannot be identified as foreshock or mainshock until a subsequent energetic aftershock is formed. In the absence of an energetic aftershock, the foreshock or mainshock is identified as provisional.
Figure 7 reports the seismic sequence of the Denali earthquake (Alaska) occurred on 3 November 2002.
The earthquake was preceded by three first order foreshocks (green stars) and by a second order foreshock (green square). As can be seen, the trendline drawn from points 1 and 2 shows a hypothetical medium―long term trend and allows estimating point 3’s magnitude (next minimum), while the intersection of the straight line passing through points 3 and 4 with the vertical line passing through the mainshock occurence point (point 5), provides the dynamic mainshock’s magnitude value. Alternatively, where the seismic sequence includes multiple first order foreshocks, the dynamic mainshock’s magnitude value is provided by the linear interpolation between them (dashed green line).
![]()
Figure 6. Short-term sequence of L’Aquila earthquake on 6 April 2009 (red star). The yellow stars indicate the strongest aftershocks in the energy accumulation phase, the green stars indicate the first order foreshocks, while the green square shows the second order foreshocks. The solid black circle indicates in the transition point from the energy accumulation to energy release phase.
![]()
Figure 7. Long-term sequence of Denali earthquake (Alaska) on 3 November 2002 (red star). The yellow stars indicate the strongest aftershocks in the energy accumulation phase, the green stars indicate the first order foreshocks, while the green square shows the second order foreshocks. The solid black circle indicates in the transition point from energy accumulation to energy release phase.
3.2. Seismic Sequence Hierarchization
The use of a hierarchization process in the seismic sequence analysis, allows locating foreshocks and mainshock during the energy release phase. More accurate data on the foreshocks formation can be obtained from the seismic grid of the energy accumulation and release phases (Figure 8) representing the cyclic pattern of reference that includes cycles of different duration.
Obtained through the hierarchization process, the graph [4] , highlights how during the energy release phase, only the energy release seismic branches of different order (1r, 2r, 3r, 4r) convey to the foreshocks (nodes F1, F2, F3) or mainshock (node M), while in the energy accumulation phase, both the energy accumulation (3a) and release (2r, 1r) seismic branches convey to the aftershock (nodes A1, A2, A3) of a previous event,
The extension of the first higher order seismic branch of the branched structure (branch 3a) up to the point of calculation allows identifying the transition point (full black circle) and the various orders foreshocks of the energy release phase. We can note how the various orders foreshocks and the mainshock are positioned above the dashed red line that represents the descending trendline drawn from the higher order seismic branch.
In some seismic sequences, it is apparent how a longer period after the last first order foreshock corresponds to a greater magnitude of the subsequent foreshock or mainshock.
3.3. Index Simplified Force (ISF)
ISF is an simple and very sensitive short-term oscillator, which can be used to monitor the strength and the developmental state of a seismic sequence and to detect the foreshocks as well as the energy accumulation phase’s trend.
ISF uses two types of seismic data: the magnitude values and the number of events recorded during the day. The greater is the variation of the magnitude
![]()
Figure 8. Seismic sequence of the L’Aquila earthquake on 6 April 2009.
values and/or of the number of events, the greater the strength of the sequence. Therefore, whenever you have a daily increase of the magnitude value due to the occurrence of a foreshock or mainshock or a number of seismic events or of both, a peak is formed on the graph, followed by a gradual reduction in the amplitude of the ISF oscillation over time.
Due to the effect of the values fluctuations above the zero line, ISF has the appearance of a seismogram where, values above zero indicate the energy release phases, while negative values indicate the energy accumulation phases. ISF’s high values are associated with an increase in the number of earthquakes and/or high magnitude values. Positive and increasing index values show an energy release phase that is being strengthened, while positive and decreasing values show an energy accumulation phase. Values close to zero show that none of the two phases is ongoing and both anticipate a trend reversal.
Figure 9 shows an example of a seismic sequence structured for ISF calculation. The graph is built taking into account the following conditions:
a) If the magnitude value increases compared with the previous day, it means that an energy release phase is ongoing (green segment) ;
b) If the value decreases, it means that there is an energy accumulation phase ongoing (red segment);
c) If the value is equal, we have the same phase as the day before.
From the graph we can infer how, as the events progress, the magnitude values are not random but follow a trend according to increasing trends up to the process reversal. We can notice also growing trend phases, characterized by increasing maximum and minimum, and decreasing trend phases characterized by decreasing maximum and minimum.
![]()
Figure 9. Seismic sequence structured for IFS calculation.
The analysis of many seismic sequences revealed the existence of three main types of trends that can be identified in advance: (a) the main trend (lasting a few years); (b) the intermediate trend (lasting several months); (c) the minor trend (lasting a few weeks). It is therefore evident that there is not only one type of trend but different trends (one inside another) according to the observation time horizon.
To calculate the ISF, we simply identify the value of the daily maximum magnitude and multiply it by the number of daily shocks, attributing a positive or negative value depending on whether the value of the maximum magnitude of the day considered is greater (green segment) or smaller compared to that of the previous day (red segment). In the case where the maximum magnitude value of the day considered is equal to the previous day’s, the previous day ISF sign is attached to ISF.
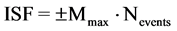 (1)
(1)
Figure 10 and Figure 11 show the ISF obtained from seismic sequences related to central Italy in 2016 and Japan in 2011.
The ISF graph related to central Italy (Figure 10) from 16 to 23 August 2016 shows low values, then a first peak due to the occurrence on 24 August (green star) of the first order foreshock whose magnitude was 6.0 Mw.
Later, after a brief energy accumulation phase highlighted by a progressive decrease of ISF values, we observe a second peak in correspondence of the second order foreshock (green star) on 26 October whose magnitude was 5.9 Mw. The positive peak is followed by a negative minimum which corresponds to the triggering point of the energy release phase (red triangle) that ends on 30 October with the mainshock whose magnitude is 6.5 Mw, which is indicated on the graph by a positive ISF peak. The epicenter of the second order foreshock on
![]()
Figure 10. Seismic sequence force index in central Italy (2016).
![]()
Table 2. Succession of earthquakes in the “Progressive Earthquakes”-type pattern (Central Italy earthquake) between 24 August and 30 October 2016.
![]()
Table 3. Succession of earthquakes in “Progressive Earthquakes”-type pattern (Central Italy earthquake) between 16 and 30 October 2016.
![]()
Figure 11. Seismic sequence and succession of earthquakes in “Progressive Earthquakes”-type pattern (Central Italy earthquake) between 16 and 30 October 2016.
26 October was located approximately 8.70 km from the main shock epicenter. The energy accumulation phase that is triggered after the mainshock is represented by a progressive and slow decrease in the oscillations amplitude of the ISF values.
Table 2 displays the short-term “Progressive Earthquakes”-type earthquakes in the energy release phase in central Italy, the occurrence time and the distance between them, while Table 3 and Figure 11 shows the impending-term pattern of the strongest earthquakes recorded in Central Italy between 16 and 30 Octo-
![]()
Figure 12. Seismic sequence force indicator of Japan earthquakes in 2011.
![]()
Table 4. Succession “Progressive Earthquakes”-type pattern earthquakes (Japan earthquake).
ber 2016, the occurrence time and the distance between them.
Figure 12 shows the ISF seismic sequence in Japan during the time window from 2 January to 31 December 2011. Up to 8 March 2011, the graph shows an initial portion of cyclical fluctuations of small amplitude, followed, on 9 March, by a first peak due to the occurrence of the foreshock with a magnitude of 7.3 Mw (green star) associated with an increase in the number of recorded events and shortly afterwards by a further ISF increase due to main shock with a magnitude of 9.0 Mw (red star) occurred on the same day. A third peak of greater amplitude is formed following the aftershock occurrence on 13 March whose magnitude was 6.6 Mw (yellow star) associated with a strong increase in the number of daily events recorded. After the 13 March earthquake, the ISF index value decrease over time and, at the end of December, they reach values similar to pre-foreshock’s on 9 March 2011.
Table 4 reports the “Progressive Earthquakes”-type pattern earthquakes in the energy release phase of the Japan earthquake.
3.4. Mainshock Magnitude Calculation
3.4.1. Graphical Method
A quick method for estimating the mainshock magnitude is shown in Figure 13
![]()
Figure 13. Short-term sequence of the earthquake occurred in the Gulf of Alaska, on 30 November 1987. Graphical procedure to determine the fluctuation range of mainshock magnitude value.
that reports the seismic sequence in the earthquake occured in the Gulf of Alaska on 30 November 1987.
As can be seen, the mainshock was preceded by a foreshock with a magnitude of 7.0 Mw recorded on l7 November 1987. To calculate the magnitude of the mainshock, the first step is to draw the branched structure [4] with its point of origin located in the foreshock and then locate on higher order seismic branch the point corresponding to 50% (point 3). From foreshock, we draw a horizontal dashed line up to meet the vertical line passing through the mainshock’s occurrence time (point 2) and thereafter, we join the point 2 with the intermediate point of the seismic branch (point 3). Finally, from the foreshock we draw its parallel line (solid black lines). The intersection of this half line with the vertical line passing through the time selected for the calculation, provides the value of the minimum expected magnitude. To calculate the maximum value, we join the points 2 and 5 of the seismic branch, then from the intermediate point 3 we draw its parallel line (solid black lines). The intersection of this parallel with the vertical line passing through the time selected for the calculation, provides the value of the maximum expected magnitude.
3.4.2. Numerical Methods
The empirical relations developed can be used to assess the magnitude of various order foreshock or “Progressive Earthquakes”-type pattern mainshock by know- ing the magnitude of the previous foreshock.
The relationships were obtained from the study of M > 3.8 foreshocks recorded by the Italian seismological network NIED network and by the USGS network between 1970 and 2016.
The average Mainshock Magnitude (MM) value is estimated through the following empirical relationship, obtained from the graphs displayed in Figure 14:
![]()
Figure 14. Relationship between foreshocks and mainshock: (a) valid for all areas of the world; (b) valid for Italy.
Relationship valid for all areas of the world with a foreshock magnitude (MF) in Mw:
![]() (2)
(2)
Relationship valid for the Italian territory with a foreshock magnitude (MF) in Mw.
![]() (3)
(3)
In the second procedure, the expected earthquake magnitude value is obtained with a formula empirically derived from a statistical analysis of the magnitude values of first and second order foreshocks that preceded the mainshocks in different areas of the world.
The equation to calculate the magnitude is as follows:
Relationship valid for all areas of the world with a foreshock magnitude (MF) in Mw:
![]() (4)
(4)
4. Conclusions
The study of various order foreshocks the “Progressive Earthquake”-type energy release phase consists of, has provided a different methods of comparison between foreshocks and big earthquakes, leading to a better understanding of the phases regulating the preparation process of strong earthquakes.
The results obtained show that in some seismic sequences, the “Progressive Earthquake”-type energy release phase tends to develop near the main shock epicenter.
In particular, the analysis of the distances in time and space between foreshocks and mainshock has highlighted how some foreshocks occur shortly before the mainshock, within a radius of 50 kilometers from its epicenter. We also pointed out how the foreshocks frequency rate decreases as the distance from the mainshock epicenter and time increase, while the magnitude values decrease as the distance and the number of days increase.
The graphical analysis of the seismic sequence has shown how the foreshocks lie above the trendline that joins decreasing magnitude maximum values that form during the energy accumulation or above the seismic branch extension whose order is greater compared to the branched structure.
An in-depth examination of the branched structure showed how during the energy release phase only the branches seismic energy release of different order convey to foreshocks or mainshock, while in the energy accumulation phase the seismic branches of both energy accumulation and release phases convey to aftershock.
ISF (Index Simplified Force) can be used to obtain information about the strength of the seismic sequence in a given moment, to locate the foreshocks and to monitor the energy accumulation and release phase progress.
Based on the data resulting from the observations of several seismic sequences, we obtained some graphical and numeric procedures to determine the mainshock’s magnitude value using the trendline, the branched structure’s higher order seismic branch or the foreshock magnitude value.
We believe that the described method shows the foreshock identification limit during seismic sequences. Actually, as is not always possible to identify the event that precedes a strong earthquake, one prefers to classify it as provisional foreshock. The subsequent evolution of the seismic sequence will provide more information so that an appropriate foreshocks classification can be implemented.
The aforementioned procedures show how, starting from the analysis of the “Progressive Earthquakes”-type energy release phase, it is possible to obtain information to locate the foreshocks and make sufficiently reliable short-term forecasts. Seismic sequence’s evolution monitoring is essential to identify correctly the foreshock that precedes strong events.