1. Introduction
The planet has been heating up in the last couple of decades and this causes large concern in society, more so since humans are allegedly responsible for the temperature rise. One of the major concerns is that we are at a point-of-no-return, caused by a positive feedback cycle of ice melting that is caused by an increased temperature and also causes further rise in temperature. The mediator of this phenomenon is the albedo―“whiteness” or reflectivity―of the Earth’s surface. Since sea water has a much lower albedo compared to ice, i.e. sea water absorbs more of the radiation received from the Sun, a melting of ice will cause an increase in absorbed radiation and thus a rise in temperature and further melting of ice. We recognize a positive feedback system that can cause a catastrophic runaway situation.
Wikipedia writes it nicely: “Ice-albedo feedback (or snow-albedo feedback) is a po- sitive feedback climate process where a change in the area of snow-covered land, ice caps, glaciers or sea ice alters the albedo. This change in albedo acts to reinforce the initial alteration in ice area. Cooling tends to increase ice cover and hence the albedo, reducing the amount of solar energy absorbed and leading to more cooling. Conversely, warming tends to decrease ice cover and hence the albedo, increasing the amount of solar energy absorbed, leading to more warming.” Such effects have long been known to result in positive feedback and an increased climate sensitivity [1] - [6] .
Indeed, the temperature has risen in the past decades, and the albedo of the Arctic region seems to have decreased until 2011 [7] [8] . Yet, the total amount of sea ice on this planet has not changed from 1979, when measurements started, until now. The Antarctic Sea Ice extent was actually in May 2014 at its maximum ever measured [9] . Images of icebreakers getting stuck in the ice make it to the headlines. Apparently, the ice coverage of our planet has varied dramatically, but somehow we are back on the same level as in 1979. There do not seem to be any signs of an avalanche effect―at least not in the data. This is remarkable, to say the least. There where a runaway scenario of melting ice that will lower the Earth’s albedo that will raise the temperature that will melt more ice is envisaged, nature shows to be quite resilient. Somehow it does manage to escape the man-imagined scenario (if not man-made scenario). At this point, it is important to point out that talking about a “trend” can only be done if the model is linear and the measurement data are so noisy as to mask the linear behavior. In case of sea ice, the measurement noise is close to zero and talking of trends therefore does not make sense. The reasoning “I only understand a trend and that is therefore reality, with any deviations from the trend defined as noise” is a logical fallacy. Nature is not linear and there is no “trend”. What you see is all there is. Deviations from the trend prove our assumptions of linearity wrong. There is something going on with the ice that we do not understand.
This made us think about what might be the underlying cause for a restoring process. A phenomenon that would cause molten ice to come back, instead of accelerating the process of melting. In this paper we present the results of our research, the things we came up with. We use finite-elements simulations to demonstrate them.
We first studied the effect of the skew angle of radiation at the polar regions com- bined with Fresnel reflectivity and see that this indeed has a negative-feedback effect. Then we studied an effect of thermal transport, both horizontal and vertical. This idea is simple and straightforward. It is based on the fact that sea water has indeed a much lower albedo, and thus absorbs more radiation, but this albedo effect is overshadowed by the effect that sea ice can be much cooler than sea water (the latter at least above melting point) because thermal transport is much lower in solid materials compared to liquid, the latter also having convection. Ice has a low thermal conductivity, in contrast to water, and the top layer of the ice―the surface that is exposed to the universe and that is radiating out―can have significantly lower temperature than water, and thus radiates much less. Heat trapped under a layer of ice cannot surface and dissipate into the universe, the ice working like a blanket. This accumulated heat will eventually melt the ice. Conversely, open seawater can be warm at the surface and emit larger amounts of radiation, efficiently cooling the planet, and enabling refreezing of the water.
In any case, what is often forgotten in the albedo argument is that anyway not much radiation is absorbed in the polar regions and the albedo effect is thus expected to be small, if not negligible. The lower temperature of ice compared to water and its resul- ting lower emission, however, is a significant contribution, since outward radiation scales with the fourth power of temperature, i.e. Stefan-Boltzmann Law of black-body radia- tion. For example, lowering the temperature by 11% from 273 K (zero ˚C, sea water) to 243 K (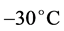 , ice surface) will cause a humongous 37% reduction in emission power, from 315 W/m2to 198 W/m2.
, ice surface) will cause a humongous 37% reduction in emission power, from 315 W/m2to 198 W/m2.
In steady state, heat to the polar regions is received not so much through inbound radiation, which is rather negligible. Firstly because of the low angle of incidence of radiation 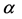 which introduces a
which introduces a 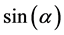 effect. Moreover, below certain angles, the reflection shoots up (and absorption declines) because of Fresnel’s equation [10] . The refractive index of water is higher than that of air―1.33 [11] vs. 1―and at normal incidence the radiation reflected off the interface between water and air is
effect. Moreover, below certain angles, the reflection shoots up (and absorption declines) because of Fresnel’s equation [10] . The refractive index of water is higher than that of air―1.33 [11] vs. 1―and at normal incidence the radiation reflected off the interface between water and air is 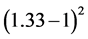
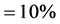 . This increases to 100% for light parallel to the surface, with a significant in- crease starting at an angle of about 70˚. Things like ripples and waves on the ocean modify this effect, but it has been estimated that the albedo of sea water varies with the Sun’s position in the sky from zenith to horizon from about 2.5% to 42.5% [12] . So, first of all, not much light is received at the polar regions to begin with, making mo- dulations of albedo insignificant, and second, the albedo does not change so drama- tically from ice (50%) to seawater (40%).
. This increases to 100% for light parallel to the surface, with a significant in- crease starting at an angle of about 70˚. Things like ripples and waves on the ocean modify this effect, but it has been estimated that the albedo of sea water varies with the Sun’s position in the sky from zenith to horizon from about 2.5% to 42.5% [12] . So, first of all, not much light is received at the polar regions to begin with, making mo- dulations of albedo insignificant, and second, the albedo does not change so drama- tically from ice (50%) to seawater (40%).
Instead, at the polar regions, most heat is received through thermal transport in the so-called Thermohaline Circulation, a moving belt of water that conveys a lot of heat to the poles. This circulation carries a tremendous amount of water and heat, estimated to be 17 sverdrup 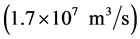 and 1.2 PW (petawatt) compared to the total global 120 PW radiation received from the Sun. A lot of heat is similarly received by at- mospheric heat transport. All in all, polar regions receive heat primarily from transport and no so much from direct absorption of solar radiation.
and 1.2 PW (petawatt) compared to the total global 120 PW radiation received from the Sun. A lot of heat is similarly received by at- mospheric heat transport. All in all, polar regions receive heat primarily from transport and no so much from direct absorption of solar radiation.
From there it radiates outward as efficiently as from any region on this planet― effectively the “albedo” of the earth is zero in the wavelength window of radiation emission, mainly infra-red. The real albedo in the visible light therefore has no impact on the outward radiation and little impact on the inward radiation.
We will now show the results of finite-elements simulations. They consist of dividing a ringlike world in many cells, each with an orientation, a temperature and an albedo and then calculate the heat dynamics.
2. Implementation
We use a finite-elements system as depicted in Figure 1. This system is a simplification of reality, but contains all of the necessary elements needed to make a correct phenomenological analysis of the real Earth system. In our system, a ring of water is made up of a large number of segments (elements). The ring itself is imagined to rotate about its polar axis. This rotation is much faster than other processes, e.g. 24 hours for a full rotation, compared to cooling/heating relaxation times in the order of years, and water fluxes in the order of thousands of years. As such, the received radiation is imme- diately averaged out over a full rotation of  in the calculation. Also, no seasonal effects are taken into account (no nutation of the rotation axis).
in the calculation. Also, no seasonal effects are taken into account (no nutation of the rotation axis).
In the simplest simulations, each element is in radiation balance. The incoming radiation is governed by the angle 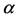 of the position of the element relative to the equator; at the equator
of the position of the element relative to the equator; at the equator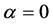 . The Sun is far away in the plane of the equator and
. The Sun is far away in the plane of the equator and
![]()
Figure 1. Schematic drawing of the system studied with the definitions of the parameters and variables.
radiates with a solar constant of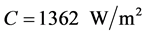 . The amount of absorbed energy per square meter
. The amount of absorbed energy per square meter  per second is then determined by this angle
per second is then determined by this angle  and the albedo
and the albedo 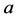 of the element, and further averaged out by the rotation around the vertical axis
of the element, and further averaged out by the rotation around the vertical axis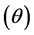 . The latter also suffering from the effect that half of the time the radiation received is zero because it is in the shadow:
. The latter also suffering from the effect that half of the time the radiation received is zero because it is in the shadow:
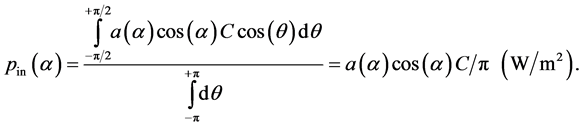 (1)
(1)
The amount of energy emitted is independent of the angles 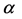 and
and 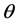 and is also independent of the albedo. Where the albedo is defined as the whiteness in the visible light, the emission of an element is in the infrared window of the electromagnetic spec- trum, and it is assumed that all materials on Earth are “black” in the infrared and emit therefore like a black body,
and is also independent of the albedo. Where the albedo is defined as the whiteness in the visible light, the emission of an element is in the infrared window of the electromagnetic spec- trum, and it is assumed that all materials on Earth are “black” in the infrared and emit therefore like a black body,
![]() (2)
(2)
with ![]() the absolute temperature and
the absolute temperature and ![]() the Stefan-Boltzmann constant (5.670373 × 10−8 Wm−2K−4). This reasoning is close to the truth and has led for instance to the conclusion―common belief―that a change of real visible-light albedo―as in melting white snow to black seawater―will not alter the emission, but will significantly alter the absorption, and an aggravation of global warming is expected, as mentioned in the introduction.
the Stefan-Boltzmann constant (5.670373 × 10−8 Wm−2K−4). This reasoning is close to the truth and has led for instance to the conclusion―common belief―that a change of real visible-light albedo―as in melting white snow to black seawater―will not alter the emission, but will significantly alter the absorption, and an aggravation of global warming is expected, as mentioned in the introduction.
The depth of the ring of water is chosen to be 100 m, since that is a reasonable number for the water on Earth that contributes to the climate cycle, the so-called ocean mixed layer [13] . This is important only for the time constant of the relaxation; taking deeper or shallower rings would only alter the time constants, but not alter the final temperatures. The width is taken to be 100 meters, but this parameter does not in- fluence the calculations at all (everything scales linearly with the width) and is only given for completeness’ sake and to be able to visualize a 3D object.
The advanced simulations also include water circulation that, combined with a heat gradient, will cause transport of heat to the polar regions. Alternatively, we also simu- late with a heat conduction mechanism that occurs also in still water and for which no circulation is needed, even though we know that this must be of a much smaller order of magnitude.
Note that no greenhouse effects are taken into account. Basically, there is no atmos- phere. We are not simulating the greenhouse and the full climate here. We are only determining the effects of albedo and albedo changes on the temperature and, more specifically, on the amount of sea ice. To compensate for the lack of atmosphere and have anyway somewhat Earth-like temperatures in the simulations, we “crank up” the inward radiation by multiplying it with a “fudge factor”.
In the first step, we make a simulation without any effects. Each element has the same steady albedo that is not a function of temperature. In the second step, we intro- duce the simple albedo effect; an element with temperature dropping below zero celsius will change the albedo from low to high, and vice versa. To better demonstrate the effect, we make, apart from a simulation with realistic changes in albedo (40% to 50%), also a simulation with exaggerated changes from 0% to 60%, as society is wont to belief. This indeed shows a non-reversible “hysteresis” effect, where the final situation de- pends on the starting conditions. In the third step, we include a more realistic Fresnel albedo, as mentioned before, and show that this mitigates the hysteresis effect. In the final simulation, we introduce the concept of heat transport. This nearly completely removes the hysteresis effect and ice, once removed, simply reappears in a time scale of about ten years.
3. Results
The first simulation is a system that does not include albedo changes. All albedos are taken to be 31%. Nor does the simulation include circulation of water and accom- panying transport of heat. In this simulation all elements start at the same temperature, 273.16 K (the triple point of water, TPW), and the system is allowed to relax. For every element, the input and output radiation are calculated, a function of its position and temperature, respectively (Equations (1) and (2)). The average temperature in this way was found to be −22˚C when mapped to a spherical planet (every segment enters into the average with a weight![]() , with
, with ![]() the latitude). To mimic an atmos- phere―to give values closer to real-life―a “fudge factor” of 1.75 was introduced in the inbound radiation, which then resulted in Figure 2 and an average temperature of 15.4 celsius.
the latitude). To mimic an atmos- phere―to give values closer to real-life―a “fudge factor” of 1.75 was introduced in the inbound radiation, which then resulted in Figure 2 and an average temperature of 15.4 celsius.
As can be seen, the equator will warm up and saturate to about 35 degrees. Moderate regions saturate at about 10 degrees and the poles, because of total absence of input radiation will tend toward zero kelvin, which they will eventually reach. Figure 2(b) shows the temperature distribution over the ring from equator to poles after 500 kiloday.
The characteristic relaxation time of cooling and warming depends on the heat
![]()
Figure 2. Simple model. No albedo changes ![]() and no circulation. (a) Temperature transients when star- ting at 273 K for three key latitudes. (b) Temperature after 500 kiloday (ten times window of left panel) as a function of latitude. (“Eq.” is “Equator”, “NP” and “SP” are North Pole and South Pole, respectively).
and no circulation. (a) Temperature transients when star- ting at 273 K for three key latitudes. (b) Temperature after 500 kiloday (ten times window of left panel) as a function of latitude. (“Eq.” is “Equator”, “NP” and “SP” are North Pole and South Pole, respectively).
capacity of the layer used and thus its thickness and specific heat. The latter is well known for water, but the effective thickness is something that can be discussed. How- ever, our value of 100 m is in line with values given in the literature and we can thus expect that the relaxation time found here―in the order of some years―is close to the real one of the climate system of our planet. Note, however, that the value is much smaller than the time scale predicted by the majority of climate researchers that predict changes in CO2 concentration in the atmosphere to become apparent on the scale of centuries.
In the next simulation, we include the change of albedo between water and ice. Common knowledge is that water has an albedo of about 0.02 and ice 0.35. (Note that albedo of ice is much lower than the albedo of snow, the latter having an albedo between 0.45 [old] and 0.85 [fresh]). The results are shown in Figure 3. A hysteresis
![]()
Figure 3. A system with albedo changes from sea (0.02) to ice (0.35) when the temperature drops below TPW. The final situation depends on the history; Starting with high temperature (a marginally frozen planet, (a) and (b)) less of the planet is covered with ice compared to a slightly lower starting temperature (a marginally unfrozen planet, (c) and (d); fudge factor 1.306). The insets show the distribution of ice (white) and water (dark) in the ring.
effect now occurs in that the final result also depends on the starting conditions, the history of the planet. If we start with a marginally frozen planet (Figure 3(a) and Figure 3(b)), the system winds up with an average temperature of 6.6 degrees celsius and the planet frozen from 30.9 degrees latitude up (see inset of panel b). If, instead, we start with a fully unfrozen planet (Figure 3(c) and Figure 3(d)), the planet winds up with an average temperature of 15.4 degrees celsius and covered with ice from 55.3 degrees latitude up. There is indeed a huge non-reversibility hysteresis in the climate system, both in temperature (8.8 degrees) and ice coverage.
The simulations above (Figure 3) summarize the common knowledge about positive feedback effect of the ice on our planet. We will now present our new ideas here.
First of all, the value for albedos of sea and ice are for perpendicular light. While reflection from ice is rather diffuse and the angle of incidence should not matter much, reflection off water has a more specular nature and the albedo depends heavily on the angle of incidence. At high angles of incidence, close to the poles, nearly all light is reflected. So, we expect a water albedo that is much higher close to the poles compared to the equator. Moreover, because the Earth is rotating, even at the equator, at some moments of the day light is effectively reflected off the water and even at the equator we can expect a higher albedo than 0.02.
Adequate is to use Fresnel’s Equation for reflection of light at the interface of two media with different refractive indices, ![]() and
and![]() , respectively. Assuming no ima- ginary part in the refractive index of water (effectively seeing it as a non-absorptive, non-attenuating medium), the reflectivity (albedo) for unpolarized light is given by [10] :
, respectively. Assuming no ima- ginary part in the refractive index of water (effectively seeing it as a non-absorptive, non-attenuating medium), the reflectivity (albedo) for unpolarized light is given by [10] :
![]() (3)
(3)
For air we can take ![]() and sea water has a refractive index equal to
and sea water has a refractive index equal to![]() , which gives us a reflection as a function of angle as in Figure 4(a), where the reflec- tivity varies from 0.0201 (a value close to the 0.02 used before, justifying our as- sumption of a non-imaginary refraction index) to 1. Note that waves can change this
, which gives us a reflection as a function of angle as in Figure 4(a), where the reflec- tivity varies from 0.0201 (a value close to the 0.02 used before, justifying our as- sumption of a non-imaginary refraction index) to 1. Note that waves can change this
function-in first order spread it, equalize it, and make it less pronounced―but as long as the reflection is specular, the shape is as given here. Likewise, seasonal changes (not included in these simulations) would smear out the effect in a similar way. We continue with a waveless ocean, to test the hypothesis of albedo effects.
On basis of Fresnel Equation (Equation (3) and shown in Figure 4(a)) we can cal- culate an effective albedo at every latitude. We do this by calculating the angle ![]() of solar radiation for latitude
of solar radiation for latitude ![]() at every Earth rotation angle
at every Earth rotation angle ![]() and calculating the reflectivity according to Equation (3). The effective albedo at latitude
and calculating the reflectivity according to Equation (3). The effective albedo at latitude ![]() is then the reflectivity thus calculated averaged over
is then the reflectivity thus calculated averaged over![]() . The angle
. The angle ![]() is found by calculating the rotation matrices for rotations
is found by calculating the rotation matrices for rotations ![]() and
and![]() , applying it to the x-vector (the direction of the Sun) and then taking the dot product with the x-vector. This way we found that
, applying it to the x-vector (the direction of the Sun) and then taking the dot product with the x-vector. This way we found that
![]() (4)
(4)
The effective albedo is then given by
![]() (5)
(5)
The result of this is shown in Figure 4(b). We can see here two important effects. First of all, the albedo at the poles is unity. Meaning that polar sea water reflects sunlight even better than snow or ice does (for comparison also shown). Second, the equatorial water has, because of this specular reflection character, an albedo that is much higher than the often-assumed albedo of 0.02. That is because also these regions get the light at a very oblique angle part of the day. The effective albedo at the tropical regions is therefore about 0.12.
The implication of the high polar albedo is that the presence of ice in polar regions actually decreases the albedo and this is thus a negative-feedback “Gaia” effect; when the temperature increases ice melts and this increases the albedo and lowers the tem- perature of the planet, refreezing the water into ice again. Analyzing the figure, this happens for latitudes higher than around 70 degrees. Ice in moderate and warmer regions does have the traditional positive feedback effect. This might well be the negative feedback that we mentioned in the introduction.
On basis of this we made simulations. If the temperature of an element drops below zero ˚C, it will be attributed the albedo of ice![]() . If it melts, it gets attributed the Fresnel albedo of Figure 4. We find that, indeed, independent of the starting condition (be it a fully frozen planet, or a fully liquid planet) the polar regions wind up covered with ice. There is only a hysteresis effect for latitudes outside the polar regions, as can be seen in Figure 5. The hysteresis effect of Figure 3 of 8.6 degrees celsius has thus been reduced to 1.5 degrees. It could be absent altogether in a system without ice in the moderate regions, as is the case of our planet. We conclude that the common belief of a runaway scenario of irreversible melting of ice solely based on the albedo effects is not necessarily true.
. If it melts, it gets attributed the Fresnel albedo of Figure 4. We find that, indeed, independent of the starting condition (be it a fully frozen planet, or a fully liquid planet) the polar regions wind up covered with ice. There is only a hysteresis effect for latitudes outside the polar regions, as can be seen in Figure 5. The hysteresis effect of Figure 3 of 8.6 degrees celsius has thus been reduced to 1.5 degrees. It could be absent altogether in a system without ice in the moderate regions, as is the case of our planet. We conclude that the common belief of a runaway scenario of irreversible melting of ice solely based on the albedo effects is not necessarily true.
Yet, the question arises whether this model system is adequate for the Earth radiation system? This question is more so valid considering the fact that apparently the ice cover in the North Pole region recovered 60% in a single year, from 2012 to 2013. This hints at a much larger negative feedback effect than demonstrated above. In the next
![]()
Figure 5. Model with albedo changes. Once water freezes, its albedo changes to 0.35. Liquid water has a Fresnel albedo depending on the latitude as shown in Figure 4. (Fudge factor 1.62).
simulations another idea is tested. It adds two basic phenomena to the system (see Figure 6 for all processes): 1) Heat is transported horizontally across the globe (indi- cated by arrows), 2) Heat is transported vertically from the bottom to the top. The first one is something similar to the global thermohaline conveyor belt (THC), which we model with a simple exchange of heat between neighboring cells, heat flow is simply proportional to the temperature difference between neighboring cells. For the second effect of vertical transport, we have to add the possibility of a vertical gradient. We do this by duplicating the belt into two layers; every element is consisting of a top cell and a bottom cell. The effect we are trying to simulate is that ice not only has the property of a different albedo and associated change in absorbed light compared to water, but also a different heat conductivity. In this way, ice can cool down much more and ice, once formed, thus no longer emits much radiation and the planet heats up. In contrast, once the ice melts, heat is easily transported to the surface and radiated out, thus cooling down the planet.
To show what is going on, first we remove the formation of ice again and introduce the concept of heat transport (Figure 7). If we assume heat, ![]() , to be proportional to temperature (which it isn’t, but anyway, as will be seen, we are only interested in the gradient of heat transport and temperature), then the heat in an element is the temperature times the specific heat capacity of water
, to be proportional to temperature (which it isn’t, but anyway, as will be seen, we are only interested in the gradient of heat transport and temperature), then the heat in an element is the temperature times the specific heat capacity of water![]() , the density
, the density ![]() and the volume (
and the volume (![]() , with
, with ![]() the cross-section and
the cross-section and ![]()
![]()
Figure 6. (a) All heat effects summarized (in brackets what they depend on). Inward solar radiation (depending on angle and albedo), outward black body radiation (depending on temperature), horizontal flow of the ocean in the deep layer (depending on temperature gradient), and mixing between the deep and shallow layer (depending on the phase state of the water, solid or liquid). (b) Schematic diagram of the effect. Ice works as a blanket and reduces IR emission.
the thickness of an element). The density of heat is given by this heat divided by the volume of the element,
![]() (6)
(6)
The transport of heat, ![]() , is given by the product of heat density, the velocity
, is given by the product of heat density, the velocity ![]() of the water and the cross-section
of the water and the cross-section![]() ,
,
![]() (7)
(7)
To find out how much net heat enters an element in this way, we have to subtract what goes out from what comes in. Assuming that the same quantity of water enters and leaves an element, ![]() and
and![]() , the differential heat-flow is given by the difference of temperature of water going out and going in,
, the differential heat-flow is given by the difference of temperature of water going out and going in, ![]() , which is proportional to the temperature gradient and the thickness of an element, (
, which is proportional to the temperature gradient and the thickness of an element, (![]() , with in the limit
, with in the limit![]() ). The net heat accumulating in an element is thus
). The net heat accumulating in an element is thus
![]() (8)
(8)
The contribution of this to changes in temperature is then this heat accumulation divided by the specific heat and the volume of the element,
![]() (9)
(9)
in other words, it is the product of temperature gradient and water speed. Considering the transformation ![]() and
and![]() , this can also be translated into our ringular world coordinates,
, this can also be translated into our ringular world coordinates,
![]() (10)
(10)
with ![]() the radial velocity,
the radial velocity, ![]() (rad/s). In Figure 7 we can see how an area of the ring receives an external heat (equal to the radiation balance),
(rad/s). In Figure 7 we can see how an area of the ring receives an external heat (equal to the radiation balance), ![]() (proportional to width and distance). This extra heat is added to the incoming flux of heat
(proportional to width and distance). This extra heat is added to the incoming flux of heat ![]() and goes out of the cell as
and goes out of the cell as ![]()
Common belief is that it can take about a thousand years for a packet of water to travel around the world. That is a speed of![]() . In the simulation below, the temperature difference value is added with a factor 0.6 to the adjacent cell. To give us good results we use a temperature change of
. In the simulation below, the temperature difference value is added with a factor 0.6 to the adjacent cell. To give us good results we use a temperature change of ![]() in one step (
in one step (![]() is element number). With
is element number). With![]() , the number of elements equal to 3600 and a time step of 5 days, this gives a complete cycle in 60,000 days (164 years), which is about a factor 6 faster than what is commonly assumed. One should not forget that heat transport does not only consist of slow water flow (THC), but also induces the faster atmospheric pro- cesses which are moreover of larger magnitude overall. We therefore find our value used in the simulations reasonable.
, the number of elements equal to 3600 and a time step of 5 days, this gives a complete cycle in 60,000 days (164 years), which is about a factor 6 faster than what is commonly assumed. One should not forget that heat transport does not only consist of slow water flow (THC), but also induces the faster atmospheric pro- cesses which are moreover of larger magnitude overall. We therefore find our value used in the simulations reasonable.
Literature is often confusing about the total heat flux of our planet, but it is in the order of![]() . This is confusing since in plots for heat flux of our planet, both positive as well as negative values are given, while the transport of heat is always a positive amount, according to Equation (7). On the other hand, a heat flux derivative
. This is confusing since in plots for heat flux of our planet, both positive as well as negative values are given, while the transport of heat is always a positive amount, according to Equation (7). On the other hand, a heat flux derivative ![]() can be found by setting
can be found by setting ![]() in Equation (8), which has then units W/m instead of W. To then find the total heat flow (W), for instance from Equator to North Pole, this function has to be integrated from Equator to North Pole. Therefore, considering this confusion, more information can be obtained from the observation that the heat flux makes the equatorial regions cool down by about 14 degrees. Using the method described above, the equatorial region cools down by some 5 degrees, which is reasonable.
in Equation (8), which has then units W/m instead of W. To then find the total heat flow (W), for instance from Equator to North Pole, this function has to be integrated from Equator to North Pole. Therefore, considering this confusion, more information can be obtained from the observation that the heat flux makes the equatorial regions cool down by about 14 degrees. Using the method described above, the equatorial region cools down by some 5 degrees, which is reasonable.
Figure 8 summarizes the result of a simulation with transport of heat included. Some effects are immediately apparent. First, there are two different moderate zones, one that gets water from the Equator and is relatively warm (![]() ), and one that receives
), and one that receives
![]()
Figure 8. Model without albedo changes (all is water) but with transport of heat. Note that the poles are no longer the coldest places and that there are two distinct moderate zones, one gets a flow from the nearest pole and one from the Equa- tor. At the bottom of panel b the radiation balance is shown, the difference between inbound radiation and outbound ra- diation (Equations (1) and (2), resp.). A positive value indi- cates that the region receives more energy from the sun than it emits. (In the previous plots the radiation balance was always zero and therefore not shown).
water from a pole and is relatively cold![]() . Second, the poles themselves are much warmer than they were without circulation of heat and no longer reach absolute zero (compare with Figure 2). The final temperature plot is “averaged out”. This averaging out will cause a reduction in atmospheric and oceanic temperature gradients which are the motor for the circulation in the first place. i.e., we recognize here another stabilizing negative feed-back effect.
. Second, the poles themselves are much warmer than they were without circulation of heat and no longer reach absolute zero (compare with Figure 2). The final temperature plot is “averaged out”. This averaging out will cause a reduction in atmospheric and oceanic temperature gradients which are the motor for the circulation in the first place. i.e., we recognize here another stabilizing negative feed-back effect.
When we reintroduce the effect of ice formation and resulting albedo changes on top of this system with horizontal and vertical heat flow, we see an interesting effect, see Figure 9. Because heat can be “trapped” under the ice the outward radiation is less efficient and the planet heats up. To compensate for that, the fudge factor has been
![]()
Figure 9. Model with albedo changes and transport of heat, both vertical and horizontal (as depicted in Figure 6). The solid traces are the top layer, the dashed traces the bottom layer. Starting at a fully frozen planet, or fully unfrozen planet results in nearly the same outcome.
reduced to 1.3 to give us again somewhat Earth-like temperatures. For the mixing factor we used 100% per time step (5 days) for a liquid top layer and 1% per time step for a frozen top layer. Horizontal circulation was set at 0.06 angular degrees per time step (full circulation in 87 years).
As can be seen, the hysteresis effect has nearly completely disappeared. Starting at a fully frozen planet or fully unfrozen planet results in the same outcome, as can be seen by comparing panels b and d. Interestingly, the simulations at the edge of the ice cap are very noisy, as if smaller ice shelves are floating close to this edge. We attribute this to calculation instabilities, however, and do not claim that our system really can mimic icebergs.
The effect of the ice cap working as a blanket can be estimated from the difference between the temperature of the top layer and the bottom layer. At places where there is ice, this is easily 10 degrees, and the effect is therefore a loss of IR emission of about 50 W/m2 (Equation (2)), which is significant.
All results are summarized in Table 1.
4. Discussion
We have studied here the idea of the effect of phase changes when ice melts and water
![]()
Table 1. Summary of simulations and resulting hysteresis, when starting with a two-degree dif- ference in starting conditions, TPW ±1˚C (a fully frozen or unfrozen planet).
freezes into ice. The common idea is that these changes, through albedo changes, add positive feedback to the system; once ice disappears the effect is amplified by more heat absorption.
Contrary to this belief, we see that phase changes in fact can create negative feedback. The effects are two-fold: 1) The albedo of ice is lower than that of water at polar regions, as caused by the Fresnel effect, where water reflects all incoming radiation when the angle is at grazing incidence (with the sun close to the horizon). 2) Ice effectively blocks heat transport from lower layers of the ocean to the surface. The surface can then not radiate out the heat and the planet warms up, melting the ice.
The simulations are a proof of concept. We tried to keep here the system as simple as possible, to highlight the effects, so that everybody can easily understand what is going on. Simulations on a more realistic spherical planet with moreover an atmosphere (so as also to avoid the use of fudge factors) will have to show how much of this effect can be mapped to such a world. Things like the atmosphere [14] or non-periodic water circulation as in the ENSO (El Niño [and La Niña] Southern Oscillation) [15] have been completely ignored, along with changes in the thermohaline circulation [16] [17] [18] [19] . A more important thing that we have been ignoring is the tilt of the Earth rotation axis, which might change the game. However, we would like to point out once again that we only, and exclusively, studied the idea of water/ice phase changes and the associated albedo changes. Since we do not have access to the sophisticated equipment used in modern simulations, our contribution here is merely to point out the possibility and leave it up to others to implement them in more realistic state of the art calcu- lations.
Disclosure of Interests
The authors declare not to have any conflicts of interests. This research was paid by no grant. It received no funding whatsoever, apart from our salaries at the university where we work. Nor are we members of any climate committees (political or other) or are we linked to companies or NGOs, financially or otherwise. We are not members of any political party or movement. This is an independent work that does not necessarily represent the opinion of our university or of our government.