Modelling of a Residential Solar Energy Recuperation System Setup ()
1. Introduction
Reducing CO2 emissions is a must for the survival of the planet, to do so, a tremendous effort is underway to make this possible. Individuals, organizations, and governments are all working together to help reduce emissions and greenhouse gases. Governments have big tax incentives for individuals that install and use solar cells in their households. This caused a spike in the installation of photovoltaic systems. Photovoltaic Cells (PV) have many advantages other than reducing the pollution levels. PV can help stabilize the grid [1] and save local power companies tremendous amount of money. PV can also help in reducing costs by providing local power generation; this helps utility companies to use cheaper transformers because such transformers won’t need to support as much power as before. Another way to reduce greenhouse emissions and help curb pollution levels is to use Electric (EV) or Plugin Electric vehicles (PEV) [2] and [3] . The most common approach for capturing the solar energy is to use PV cells, other approaches do exist. For example, a project in Morocco [4] is underway. The completed phase of the project is called “Noor 1”; it uses mirrors that reflect the sun’s energy into a heat receiver that is then used to spin a heat engine. Another way to capture the sun’s energy is to store it in salt so it can be used later as it is done in Tunisia [5] . Heated salt is then used to steam water that is used to spin turbines and generate electricity. The focus of this paper will be on the traditional sun’s energy recuperation method i.e. PV cells that are the most widely used.
In a previous work we analyzed a high level description for this problem from a geographic perspective [6] . In another work [7] we analyzed the system using the Micro grid Analysis Tool HOMER Pro [8] . This analyzed problem’s target was reducing the cost of purchased electricity from the grid. This paper will address and model the complete residential setup that includes all the following components: photovoltaic cells, electric home load usage, electric vehicle, high voltage battery as an energy storage, boost, and finally inverters. Each of these components will be modelled and described. The whole system will then be presented showing the different setups that are possible when putting these components together. The next section will discuss the setup and different combinations when putting all these components together. Section 3 will describe the model each of the components of the PV system along with an EV. The paper is then ended with a future work and a conclusion.
2. PV System―Configurations
This section will get into the details of the components of the PV system and how these components can come together to form different configurations. The different components that compromise a complete PV setup for a residential system with an EV can be compromised of the following:
1) PV Cells,
2) High Voltage Battery,
3) Electric or Plugin Electric Vehicle,
4) Household Loads,
5) Boost,
6) Inverter.
Table 1 shows different configurations that are possible given the different components that make up the complete system. The common setup between all these configurations is that they all have a home load and PV cells because this is the focus of the paper.
Based on these 5 different configurations, we might use different components to setup the system that we might be designing. Configuration 1 consists of all the 6 components connected together in a fashion shown in Figure 1. In this example, the household contains an array of PV cells, a plugin electric vehicle, and a battery bank. The boost and the inverter are needed in this situation to convert low voltage from the PV cells into a higher potential so that the current can be pushed to the high voltage battery pack and to the electric vehicle. The inverter is needed so that DC voltage can be converted into AC voltage so it can be either used at the household or sold back to the local utility company.
Configuration 2 shown in Figure 2 is simpler and it only consists of PV cells connected to a home load that also includes an electric vehicle. The vehicle charges using the utility company while the PV cells supplies power to the home or to the grid or both if it is has enough power. Any extra generated energy by the PV cells that cannot be used by the house loads, or the grid will be wasted when the vehicle is fully charged or if it’s not plugged-in.
Figure 3 shows configuration 3 that is very similar to configuration 2; but this setup includes a booster. In this way the energy generated by the PV cells is boosted into a high voltage level and then used to charge the electric vehicle right away. The previous approach in configuration 2 means that the energy from the PV cells needs to convert from DC to AC, and then back to DC through the onboard vehicle charger before it can
![]()
Table 1. Different photovoltaic system configurations.
charge the battery. This process yields a lot of inefficiencies and thus a significant amount of energy is lost in the energy transfer between the PV cells and the electric vehicle battery.
Figure 4 shows the simplest and the most common configuration. It is also the cheapest as it requires the least amount of components. It constitutes of an array of PV installed on a residential household. Only an inverter is needed to convert DC voltage from the PV cells into AC, a frequency matcher is always needed to match the frequency of the grid.
Figure 5 shows configuration 5 which includes PV cells and a HV battery added to the home setup. This configuration allows the excess energy to be stored in the HV battery whenever there is no usage for it. This allows it to be used at a later time when there is a demand.
The next section will model all of the components that used in the 5 configurations listed earlier. After the components are modeled, this will provide a benchmark and a solid foundation to do further analysis on any configuration we decide to analyze.
3. PV System―Modeling
This section will model each of the components that were listed in Section 2 which is
an analysis of 5 configurations before any further analysis can be done on the system. The next subsections will model each of the components separately. The first component to model is the battery. We will then model the Electric or Plugin Electric Vehicle; photovoltaic cells will come next, followed by the inverter, booster, and finally the home load.
3.1. Battery Model
Lithium-Ion (Li-Ion) is becoming the battery chemistry of choice for most portable and energy storage applications. This is true because of many reasons. These batteries possess high energy and power densities, slow self-discharge rate, and high nominal cell voltage when compared to other chemistries. Laptops, energy storage banks, cell phones, unamend aerial vehicles, electric vehicles, plug in hybrid electric vehicles as well as many other applications use li-ion batteries as the main or secondary source of power [9] [10] [11] [12] . There are a lot of methods that have been used to model li-ion batteries; and these methods vary in complexity. The simplest model to represent a li-ion battery is shown in Figure 6. The representation presented is not very practical and is not used much. It is generally substituted with another representation. A more advanced model representing the li-ion battery is shown in Figure 7. Where RS represents the internal resistance of the battery as shown in Figure 6 and Figure 7.
Figure 7 is widely used in academic and industrial applications to represent or model a li-ion battery. It consists on a resister and a capacitor in parallel that are connected to another resister in series. This is the model that we can use in our representation for the complete PV system. More complex representations can be used to model li-ion batteries. Figure 8 shows such a representation. In general modelling of lithium-ion batteries, it can get more complex in such way that more than 2 sets of (RC connected in
![]()
Figure 6. Simplest model representing a li-ion battery.
![]()
Figure 7. Advanced model representing a li-ion battery.
![]()
Figure 8. Realistic model for a li-ion battery.
parallel) combinations can exist [13] . More advanced li-ion battery modeling can use up to n RC connected in series. But this representation is beyond the scope of this paper and will not be discussed [14] .
3.2. Electric or Plugin Electric Vehicle
The summation of forces acting on a moving vehicle is shown in (1). The principles of vehicle dynamics have been known and studied for years and the physics has already been established. This applies to any moving mass whether it’s electric or not [15] .
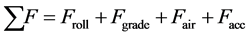 (1)
(1)
where:
1) Froll represents the rolling force i.e. the force between the vehicle tires and the road.
2) Fgrade represents the grade force. This force might be negative if the vehicle is going downhill because the gravity will be helping to propel the vehicle downwards.
3) Fair represents the air resistance of the vehicle.
4) Facc represents the acceleration force that is acting on the vehicle.
Propelling the vehicle across some distance at a specified velocity v means that the instantaneous power can be represented as shown in (2). Equation (2) is simply equation (1) multiplied by the velocity of the vehicle. Using (1) and (2) we can calculate the total energy needed for the vehicle to move some distance. This is represented as shown in (3). Equation (3) represents the energy in joules that is needed to move the vehicle for some time t (seconds) at speed v.
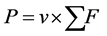 (2)
(2)
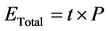 (3)
(3)
The power calculation as shown in (2) is not and almost never steady due to the fact that neither the velocity nor the forces acting on the moving mass are constant. This deems (3) as unusable as it is described. To calculate the energy consumed by the moving vehicle, integration of hundreds and thousands of energy segments is needed. These segments represent the different accelerations, speeds, different grades, rolling resistance, and other factors.
As mentioned earlier the dynamics shown in (1) is straightforward and can be represented as the following:
・ Froll (rolling resistance) can be expressed as shown in (4).
is the vehicle’s mass in kg, g is the gravitational acceleration, and fr is the tire rolling resistance coefficient. (fr is dependent on the tire pressure, tire composition, and most importantly on the driven road) [16] .
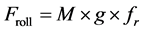 (4)
(4)
・ Fgrade is shown in (5). i represents the road grade.
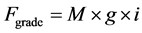 (5)
(5)
・ Fair is shown in (6). Pa is the air mass density, CD is the aerodynamic drag coefficient, Af is the frontal area of the vehicle in m2, v is the vehicle speed in m/s, and vwind is the head wind speed. Vwind can be positive or negative depending on the direction of the wind, it can also change abruptly between them as well.
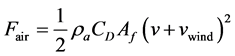 (6)
(6)
・ Facc is shown in (7). M is the vehicle’s mass in kg, δ is the rotational inertia factor, and a is the vehicle acceleration in m/s2.
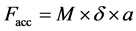 (7)
(7)
Putting Equations (4), (5), (6), and (7) back into Equation (1) and rearranging we get the total force that is acting on the vehicle. This new representation is shown in (8) below.
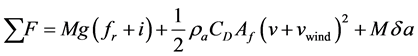 (8)
(8)
Applying the same principle as (2) on (8) i.e. multiplying (8) by the velocity yields to (9). Where (9) represents the total power acting on the moving vehicle.
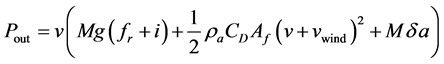 (9)
(9)
Electric vehicles are capable of regenerative braking [17] , applying this factor to (9) will yield a new energy formulation as shown in (10). α represents the factor of the total energy that can be regenerated (or stored back in the battery) by the electric motor after all the efficiencies have been applied. The regenerative braking power is marked as Pin. Regenerative energy is created whenever the driver steps on the brake pedal or when the vehicle is coasting. Lastly, the total energy acting on the vehicle is shown in (11). Equation (11) is just the summation of the total positive and negative energy acting on the vehicle.
![]() (10)
(10)
![]() (11)
(11)
3.3. Photovoltaic Cells
Different papers have studied and analyzed the modelling perspective for photovoltaic cells. Some work used Matlab and Simulink to do the analysis as shown by Salmi et al. [18] . The authors in [19] attempted to find the parameters of the nonlinear I-V equation by adjusting the curve at three points: open circuit, maximum power, and short circuit. The authors in [20] described a novel method that uses a computer simulation model which is capable of predicting the cell’s output based on changed of irradiance and temperature. Temperature has big factors on the amount of energy the solar panels can produce. It is well known that the efficiency of the solar cells increases as temperature decreases [21] . As a simple introduction a photovoltaic cell is a semiconductor diode whose p − n junction when exposed to light [22] [23] allows the flow of electrons. An ideal photovoltaic cell can be represented as shown in Figure 9 below.
The output current from the PV cell can be done using the equation:
![]() (12)
(12)
where ![]() is the short circuit current that is equal to the photon generated current
is the short circuit current that is equal to the photon generated current
![]()
Figure 9. Ideal PV cell circuit representation.
and ![]() is the current shunted through the intrinsic diode. The diode current is given by Shockley’s diode equation [24] :
is the current shunted through the intrinsic diode. The diode current is given by Shockley’s diode equation [24] :
![]() (13)
(13)
where:
1) Vd is the diode’s voltage,
2) I0 is the reverse saturation current of the diode,
3) t is the junction temperature in Kelvin,
4) q is the electro charge valued at 1.602 × 10−23,
5) k is Boltzmann’s constant valued at 1.381 × 10−23 J/K.
3.4. Inverter
The simplest way to define an inverter is to say that it converts direct current into alternating current. This is needed in our setup because the solar cells and the battery bank produce and store electric power in a direct current form and this power needs to be converted into alternating current so it can be used by the household or pushed back to the grid. Sine wave inverters represent the current technology, this is because the power delivered to the utility have the harmonics almost eliminated. One drawback is that these kind of inverters are more complicated and expensive to implement. Figure 10 shows a simple representation for a simple inverter where Tn represents the transistor switch.
3.5. Boost
A buck-boost transformer is often used to increase or decrease the voltage level to match the voltage level between 2 components. In our setup it is being used to boost the voltage between the PV cells and the high voltage energy storage battery bank and/or between the PV cells and the electric vehicle in case DC charging is performed. Figure 11 shows a simple circuit that represents a boost circuit [25] .
Figure 11 illustrates an open loop boost converter. The circuit consists of an inductor
![]()
Figure 10. Simplest form representing an inverter.
(L1), an output capacitor (Cout), a diode (D1) with an equivalent series resistance (RCout). The load is the resistor ROUT, and the switch Q1 is assumed to be ideal. We assume that VIN, VOUT, and VCOUT to be the input voltage, output voltage, and the voltage across COUT respectively. IL1 is the current across L1, and VD1 is the forward voltage drop across D1. When Q1 is switched on, the state equations are represented as the following:
![]() (14)
(14)
![]() (15)
(15)
The output equation is:
![]() (16)
(16)
when Q1 is switched off, the output equation listed above stays the same while the state equations become:
![]() (17)
(17)
![]() (18)
(18)
3.6. Home Load
The modelling of a home load is straightforward. The process works as follows: the driver returns home from work at around 5 - 6 P.M. This time is usually the peak hours for the electric grid demand [26] . When most people are at home, the demand increases; it decreases throughout the day when most people are at work. Figure 12 shows a typical home load for winter and summer days in the USA [27] . This load is significantly affected by the behavior of the people. People tend to go to work and return home at particular times mainly around 8 - 9 AM and return around 5 - 6 PM. That is why we see a peak in the energy consumption around these times.
![]()
Figure 12. Typical home load for a winter/summer day in the USA.
4. Conclusion and Future Work
This paper presented a whole system modelling and representation for a full residential system with all the different components that make up a PV residential setup with a possible EV load. All the possible configurations were presented as well. The work presented in this paper can be used a basis for future development for any optimization that can be done on the system. Furthermore, we would like to expand our work by considering optimization control methods by making sure that each component is run at its highest optimization point to improve performance, reduce costs, and deliver more renewable energy to the users. More advanced control techniques might also be considered to fulfill these tasks such as the ones described in [28] and [29] . This work has been sponsored by Shaqra University at Kingdom of Saudi Arabia.