Approximate Inertial Manifold for a Class of the Kirchhoff Wave Equations with Nonlinear Strongly Damped Terms ()
1. Introduction
It is well known that we are studying the long time behavior of the infinite dimensional dynamical systems of the nonlinear partial differential equations, and the concept of the inertial manifold plays an important role in this field. In 1985, G. Foias, G. R. Sell and R. Teman [1] first put forward the concept of the inertial manifold; it is an invariant finite dimensional Lipschitz manifold; it is exponentially attracting trajectory and contains the global attractor. But to ensure that existing conditions are very harsh for inertial manifolds (For instance, spectral interval condition), the existence of a large number of important partial differential equations is still not solved. Therefore, people naturally think of using an approximate, smooth and easy to solve the manifolds to approximate the global attractor and inertial manifolds, which is the approximate inertial manifold.
Approximate inertial manifolds are finite dimensional smooth manifolds, and each solution of the equation is in a finite time to its narrow field. In particular, the global attractor is also included in its neighbourhood. The existence of approximate inertial manifolds of a large number of dissipative partial differential equations has been studied [2] - [7] .
In this paper, we are concerned a class of the Kirchhoff wave equations with nonlinear strongly damped terms referred to as follows:
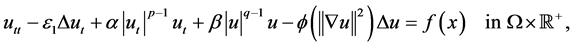 (1.1)
(1.1)
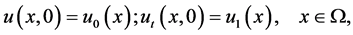 (1.2)
(1.2)
 (1.3)
(1.3)
where  is a bounded domain in
is a bounded domain in 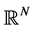 with smooth boundary
with smooth boundary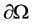 , and
, and 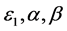 are positive constants, and the assumptions on
are positive constants, and the assumptions on 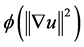 will be specified later.
will be specified later.
In [8] , G. Kirchhoff firstly proposed the so called Kirchhoff string model in the study nonlinear vibration of an elastic string. Kirchhoff type wave equations have been studied by many scholars (see [9] [10] [11] ). In reference [12] , the long time behavior of solutions for the initial value problems (1.1) - (1.3), the existence of global attractor corresponding to the semigroup operator 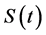 and the dimension estimation of glo- bal attractor, have been researched.
and the dimension estimation of glo- bal attractor, have been researched.
In [13] , Dai Zhengde, Guo Boling, Lin Guoguang studied the fractal structure of attractor for the generalized Kuramoto-Sivashinsky equations:
 (1.4)
(1.4)
 (1.5)
(1.5)
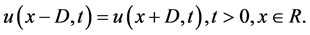 (1.6)
(1.6)
where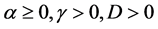 .
.
In [14] , Li Yongsheng, Zhang Weiguo studied regularity and approximate of the attractor for the strongly damped wave equation:
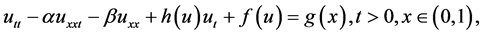 (1.7)
(1.7)
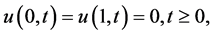 (1.8)
(1.8)
 (1.9)
(1.9)
where 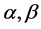 are positive constants.
are positive constants.
Luo Hong, Pu Zhilin and Chen Guanggan [15] studied regularity of the attractor and approximate inertial manifold for strongly damped nonlinear wave equation:
![]() (1.10)
(1.10)
![]() (1.11)
(1.11)
![]() (1.12)
(1.12)
where ![]() is a positive constant.
is a positive constant.
Wang Lei, Dang Jinbao and Lin Guoguang [16] also studied the approximate inertial manifolds of the fractional nonlinear Schrödinger equation:
![]() (1.13)
(1.13)
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
where ![]() is a standard orthogonal base,
is a standard orthogonal base,
i is the imaginary unit.![]() .
.
Recently, Sufang Zhang, Jianwen Zhang [17] studied approximate inertial manifold of strongly damped wave equation:
![]() (1.16)
(1.16)
![]() (1.17)
(1.17)
![]() (1.18)
(1.18)
where ![]() is a bounded domain in
is a bounded domain in ![]() with smooth boundary
with smooth boundary![]() ,
, ![]() is a constant, the function
is a constant, the function![]() .
.
The paper is arranged as follows. In Section 2, we state some assumptions, notations and the main results are stated. In Section 3, through the estimation of solution smoothness of higher order, then we obtain the regularity of the global attractor. In Section 4, by constructing a smooth manifold, namely the approximate inertial manifold, we approximate the global attractor for the problems (1.1) - (1.3).
2. Statement of Some Assumptions, Notations and Main Results
For convenience, we denote the norm and scalar product in ![]() by
by ![]() and
and![]() ;
;
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
Let![]() , where
, where ![]() is a bounded domain, where the norm is defined as
is a bounded domain, where the norm is defined as![]() .
. ![]() is an unbounded positive definite self adjoint operator. Let
is an unbounded positive definite self adjoint operator. Let ![]() , From reference [25] ,
, From reference [25] , ![]() is compact,
is compact, ![]() is dense in E, so
is dense in E, so![]() , where E is space by
, where E is space by ![]() as base generated.
as base generated. ![]() , where
, where![]() ,
, ![]() are the eigenvalues and eigenvectors of A,
are the eigenvalues and eigenvectors of A, ![]() ,
,![]() . Then
. Then ![]() consists of a set of standard orthogonal basis space E.
consists of a set of standard orthogonal basis space E.
We present some assumptions and notations needed in the proof of our results as follows:
(G1) From reference [12] , we set some constants:![]() ,
,
such that![]() ,
,![]() .
.
(G2) Let![]() , and
, and![]() ,
,![]() .
.
Theorem 2.1 From reference [12] , due to (G1), (G2) hold,
(i) Let![]() , then for each
, then for each![]() ,
, ![]() , the problems (1.1)-(1.3) exist solution u,
, the problems (1.1)-(1.3) exist solution u,![]() ;
;![]() ,
,![]() .
.
(ii) Let![]() ,
, ![]() is the semigroup operator for the problems (1.1) - (1.3), then the semigroup
is the semigroup operator for the problems (1.1) - (1.3), then the semigroup ![]() exists a compact global attractor
exists a compact global attractor![]() . So we can find a compact connected invariant set B to absorb all the bounded sets on
. So we can find a compact connected invariant set B to absorb all the bounded sets on![]() .
.
3. The Regularity of Global Attractor
In order to obtain the regularity of global attractor, we need to give a higher order uniform a priori estimates for the solution.
Let![]() , then the problem (1.1) can be reduced to the following form:
, then the problem (1.1) can be reduced to the following form:
![]() (3.1)
(3.1)
![]() (3.2)
(3.2)
Let
![]() (3.3)
(3.3)
where![]() .
.
Further, we rewrite the problems (1.1) - (1.3):
![]() (3.4)
(3.4)
Each![]() , the solution to the problems (1.1) - (1.3) meet the following conditions:
, the solution to the problems (1.1) - (1.3) meet the following conditions:
![]() (3.5)
(3.5)
And there exist ![]() such that the following inequalities are established:
such that the following inequalities are established:
![]() (3.6)
(3.6)
where![]() ,
, ![]() is independent of the initial value
is independent of the initial value![]() .
.
Proof. By the first conclusion (i) of theorem 2.1, when![]() , the solution u meet:
, the solution u meet:![]() ,
, ![]() ,
,![]() . By the second conclusion (ii) of theorem 2.1, there exist
. By the second conclusion (ii) of theorem 2.1, there exist![]() , when
, when![]() ,
,
![]() (3.7)
(3.7)
Meanwhile, ![]() is uniformly bounded in E,
is uniformly bounded in E,![]() .
.
![]() (3.8)
(3.8)
Then![]() ,
,![]() .
.
Based on the reference [27] , the analytic properties of the semigroups generated by ![]() and the Equation (3.4), immediately get
and the Equation (3.4), immediately get![]() , the solution
, the solution![]() , furthermore, for the non-homogeneous term
, furthermore, for the non-homogeneous term ![]() in the Equation (3.4),
in the Equation (3.4), ![]() , then
, then![]() ,
, ![]() , due to
, due to ![]() are arbitrary,
are arbitrary, ![]() ,
,![]() .
.
Since![]() , we are now considering
, we are now considering![]() , respectively, as the initial time, initial value. Next, we consider the equation about
, respectively, as the initial time, initial value. Next, we consider the equation about![]() ,
,
![]() (3.9)
(3.9)
then
![]() (3.10)
(3.10)
![]() (3.11)
(3.11)
![]() (3.12)
(3.12)
![]() (3.13)
(3.13)
Next, we multiply ![]() with both sides of the equation (3.10) and integrate over
with both sides of the equation (3.10) and integrate over ![]() to obtain
to obtain
![]() (3.14)
(3.14)
![]() (3.15)
(3.15)
![]() (3.16)
(3.16)
where from the hypothesis (G2),
![]() (3.17)
(3.17)
![]() (3.18)
(3.18)
![]() (3.19)
(3.19)
![]() (3.20)
(3.20)
![]() (3.21)
(3.21)
where![]() .
.
By using Gagliardo-Nirenberg’s embedding inequality, Hölder’s inequality:
![]() (3.22)
(3.22)
Similar to the relation (3.20):
![]() (3.23)
(3.23)
By using Hölder’s inequality, Young’s inequality and Sobolev’s embedding inequality:
![]() (3.24)
(3.24)
![]() (3.25)
(3.25)
![]() (3.26)
(3.26)
![]() (3.27)
(3.27)
In reference [12] , ![]() are bounded by a priori estimates.
are bounded by a priori estimates.
![]() (3.28)
(3.28)
So we get:
![]() (3.29)
(3.29)
From above, we have
![]() (3.30)
(3.30)
![]() (3.31)
(3.31)
Taking![]() , then
, then
![]() (3.32)
(3.32)
![]() (3.33)
(3.33)
At last, we get:
![]() (3.34)
(3.34)
Let![]() ;
;![]() ;
;
![]() ;
;
![]() .
.
By using Poincaré’s inequality, we get
![]() (3.35)
(3.35)
We take proper![]() , such that:
, such that:
![]()
Then
![]() (3.36)
(3.36)
From the relation (3.36), we can get
![]() (3.37)
(3.37)
By using Gronwall’s inequality, we obtain:
![]() (3.38)
(3.38)
Taking![]() , such that
, such that![]() , then
, then
![]() (3.39)
(3.39)
where
![]() (3.40)
(3.40)
Meanwhile, we once again take proper![]() , such that:
, such that:
![]()
So there are![]() , which make the following inequalities:
, which make the following inequalities:
![]() (3.41)
(3.41)
where![]() ,
, ![]() is independent of the initial value
is independent of the initial value![]() .
.
![]() (3.42)
(3.42)
And there exist![]() ,
, ![]() such that the following inequalities are established:
such that the following inequalities are established:
![]() (3.43)
(3.43)
Proof. Take proper T, such that![]() ,
, ![]() , we are now considering the Equation (3.9), assume (G1), (G2) hold,
, we are now considering the Equation (3.9), assume (G1), (G2) hold, ![]() ,
, ![]() ,
, ![]() , the nonlinear term
, the nonlinear term![]() . Based on the reference [27] , the solution to the Equation (3.9):
. Based on the reference [27] , the solution to the Equation (3.9):![]() . From (3.4), we get
. From (3.4), we get ![]() , due to
, due to ![]() are arbitrary,
are arbitrary, ![]() ,
,
![]() , and then we can get
, and then we can get![]() ,
, ![]() ,
,![]() .
.
Similar to lemma (3.1), we are now considering![]() , respectively, as the initial time, initial value. Next, and once again, we consider the Equations (3.9) - (3.13), multiplying
, respectively, as the initial time, initial value. Next, and once again, we consider the Equations (3.9) - (3.13), multiplying ![]() with both sides of the equation (3.10) and integrating over
with both sides of the equation (3.10) and integrating over ![]() to obtain
to obtain
![]() (3.44)
(3.44)
![]() (3.45)
(3.45)
![]() (3.46)
(3.46)
where from the hypothesis (G2),
![]()
![]()
Similar to lemma 3.1
![]() (3.47)
(3.47)
![]() (3.48)
(3.48)
By using Hölder’s inequality, Young’s inequality and Sobolev’s embedding inequality:
![]()
![]()
![]()
![]()
Through similar methods above
![]()
![]()
![]()
From above, we have
![]() (3.49)
(3.49)
![]() (3.50)
(3.50)
Taking![]() , then
, then
![]()
At last, we get:
![]() (3.51)
(3.51)
Let![]() ;
;![]() ;
;
![]() ;
;
![]() .
.
By using Poincaré’s inequality, we get
![]() (3.52)
(3.52)
We take proper![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , such that:
, such that:
![]()
Then
![]() (3.53)
(3.53)
From the relation (3.53), we can get
![]() (3.54)
(3.54)
By using Gronwall’s inequality, we obtain:
![]() (3.55)
(3.55)
Taking![]() , such that
, such that![]() , then
, then
![]() (3.56)
(3.56)
where
![]() (3.57)
(3.57)
Meanwhile, we once again take proper![]() ,
, ![]() , such that:
, such that:
![]()
So there are![]() , which make the following inequalities:
, which make the following inequalities:
![]() (3.58)
(3.58)
where ![]() is independent of the initial value
is independent of the initial value![]() .
.
Similar to above discussions, there are![]() ,
, ![]() , which make the following inequalities:
, which make the following inequalities:
![]() (3.59)
(3.59)
where ![]() is independent of the initial value
is independent of the initial value![]() .
.
Using the original Equation (1.1), we obtain
![]() (3.60)
(3.60)
Next, using the elliptic property of the operator A, we get:
![]() (3.61)
(3.61)
where ![]() is independent of the initial value
is independent of the initial value![]() .
.
So there are![]() ,
, ![]() , which make the following inequalities:
, which make the following inequalities:
![]() (3.62)
(3.62)
where ![]() is independent of the initial value
is independent of the initial value![]() .
.
According to Lemmas 3.1, 3.2, we can get the following theorem :
Theorem 3.1 From reference [14] , let ![]() is the semigroup operator for the pro- blems (1.1) - (1.3), then the semigroup
is the semigroup operator for the pro- blems (1.1) - (1.3), then the semigroup ![]() exists a compact global attractor
exists a compact global attractor ![]() in
in![]() , and
, and![]() .
.
The proof of theorem 3.1 see ref. [14] , is omitted here.
4. The Approximate Inertial Manifold for the Global Attractor
In this section, we first construct a smooth manifold![]() , and then prove that
, and then prove that ![]() is an approximate inertial manifold of the semigroup
is an approximate inertial manifold of the semigroup![]() , namely, the arbitrary trajectory of the Kirchhoff wave equations goes into a small neighbourhood of the approximate inertial manifold after large time.
, namely, the arbitrary trajectory of the Kirchhoff wave equations goes into a small neighbourhood of the approximate inertial manifold after large time.
Let![]() ,
, ![]() is an orthogonal projection from the space E to the subspace spanned by
is an orthogonal projection from the space E to the subspace spanned by![]() ,
, ![]() , so that u is decomposed as the sum
, so that u is decomposed as the sum![]() .
.
For the solution u of the problems (1.1) - (1.3), let![]() ,
, ![]() ,
, ![]() ,
,![]() . Then
. Then![]() ,
, ![]() ,
, ![]() ,
,![]() . We use
. We use ![]() and
and ![]() to act the problem (1.1) respectively.
to act the problem (1.1) respectively.
![]() (4.63)
(4.63)
![]() (4.64)
(4.64)
Let![]() ,
,![]() . Then the problems (4.63) - (4.64) can be written as:
. Then the problems (4.63) - (4.64) can be written as:
![]() (4.65)
(4.65)
![]() (4.66)
(4.66)
From above, we have![]() , there exist
, there exist![]() ,
, ![]() , is independent of the initial value
, is independent of the initial value![]() , and then
, and then![]() ,
, ![]() So for
So for![]() ,
, ![]() , we obtain
, we obtain
![]() (4.67)
(4.67)
Remark 4.1. For the problem (4.66), if we do not consider ![]() and
and ![]() contained in the nonlinear terms, for
contained in the nonlinear terms, for![]() , we define mapping
, we define mapping![]() :
:![]() .
. ![]() is the solution of the Equation (4.68):
is the solution of the Equation (4.68):
![]() (4.68)
(4.68)
Then![]() :
: ![]() is a smooth map, its image is
is a smooth map, its image is ![]() , which is a approximate inertial manifold of the semigroup
, which is a approximate inertial manifold of the semigroup![]() .
.
Proof. Firstly, let![]() , then
, then![]() ,
, ![]() are the solutions of the problems (4.65) - (4.66), and then let
are the solutions of the problems (4.65) - (4.66), and then let![]() .
.![]() .
.
From the relation (4.68), we can obtain:
![]() (4.69)
(4.69)
![]() (4.70)
(4.70)
Then from the hypothesis (G1),![]() .
.
![]() (4.71)
(4.71)
![]() (4.72)
(4.72)
![]() (4.73)
(4.73)
We put ![]() into the relation (4.68), the following relations can be obtained immediately,
into the relation (4.68), the following relations can be obtained immediately,
![]() (4.74)
(4.74)
![]() (4.75)
(4.75)
Therefore
![]() (4.76)
(4.76)
![]() (4.77)
(4.77)
Then
![]() (4.78)
(4.78)
So, we obtain
![]() (4.79)
(4.79)
A similar method in reference [14] , we immediately get the semigroup ![]() exists a compact global attractor
exists a compact global attractor ![]() in
in![]() , and
, and![]() , and then
, and then ![]() , there exists
, there exists![]() ,
, ![]() is sufficiently large,
is sufficiently large,![]() . When
. When![]() , arbitrary trajectory arising from the
, arbitrary trajectory arising from the ![]() for the Kirchhoff wave equations, which track into a
for the Kirchhoff wave equations, which track into a ![]() neighborhood in
neighborhood in![]() .
.
![]() (4.80)
(4.80)
where the ![]() is a smooth manifold that we construct, which is very precise, to approximate inertial manifold of the semigroup
is a smooth manifold that we construct, which is very precise, to approximate inertial manifold of the semigroup![]() .
.
Acknowledgements
The authors express their sincere thanks to the anonymous reviewer for his/her careful reading of the paper, giving valuable comments and suggestions. These contributions greatly improved the paper. This work is supported by the Nature Science Foundation of China (No. 11561076).