Received 30 August 2016; accepted 26 September 2016; published 29 September 2016

1. Introduction
Nowadays, it is widely believed that the Kerr metric does not represent the spacetime of a rotating astrophysical object. It seems that there is no reasonable perfect fluid inner solution which serves as source of this spacetime [1] . Moreover, the relationship between its multipole moments and its angular momentum may not represent correctly the external field of any realistic stars [2] .
The Ernst formalism [3] and the Hoenselaers-Kinnersley-Xanthopoulos (HKX) transformations [4] are very useful to find exact axial solutions of the Einstein field equations (EFE). These formalisms allow to include desirable characteristics (rotation, multipole moments, magnetic dipole, etc.) to a given seed metrics. In this article, we develop a perturbative method by means of the Lewis metric [5] to find solutions with quadrupole moment, using the Kerr spacetime as seed metric. Our method consists in modifying four potential functions of the Lewis metric and maintaining the cross term potential function. This method was applied successfully in obtaining other approximative metrics [6] - [8] .
To ensure the validity of a metric, the given metric is expanded to its post-linear form and compared with the post-linear version of the Hartle-Thorne (HT) spacetime [9] [10] . The reason is that it is possible to find an inner solution corresponding to the HT metric [11] . This new approximation can be considered as an improvement of the HT spacetime, because it has spin octupole and the HT has not this one. There are several exact metrics [12] [13] , but these ones are more appropriate for numerical works. This Kerr-like metric has a simple form and can be useful for theoretical works. For instance, it may used to investigate the influence of the mass quadrupole in the light propagation and the light cone structure of this Kerr-like spacetime [14] .
This paper is organized as follows. Our perturbation method of the Kerr metric using the Lewis one is discussed in section 2. In section 3, it is shown that the application of this method leads to a new approximate solution to the EFE with rotation and quadrupole moment. It is checked by means of a REDUCE program that the resulting metric is a solution of the EFE [15] , and this program is available upon request. In section 4, the exterior HT metric is briefly explained and compared to our Kerr-like ones. We also compare it with the Erez-Rosen (ER) metric [5] without rotation. The comparison of our metric to the HT spacetime assures that our metric has astrophysical meaning. A comparison with other stationary metrics is given in section 5. A summary and discussion of the results is presented in section 6.
2. The Perturbing Method for the Kerr Metric
First of all, we need a spacetime to work on. To this end, the Lewis metric is chosen and is given by [5]
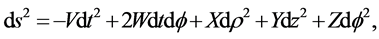 (1)
(1)
where the chosen canonical coordinates are 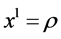 and
and . The potentials
. The potentials ,
, 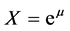 and
and  are functions of
are functions of 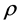 and z with
and z with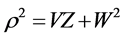 . Taking
. Taking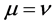 , performing the following changes of potentials
, performing the following changes of potentials 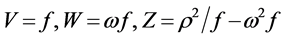 and choosing
and choosing , one get the Weyl-Papapetrou metric [5]
, one get the Weyl-Papapetrou metric [5]
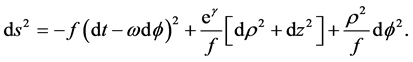 (2)
(2)
The Ernst formalism and HKX transformation are based on this metric. Here, these formalisms are not employ to generate a new one. Rather, a new method to find a Kerr-like metric with quadrupole is developed. To this goal, we use the known transformation that leads to the Kerr metric [5]
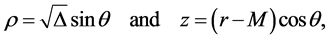 (3)
(3)
where 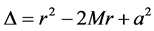 (with M as the mass of the object and a as the rotation parameter).
(with M as the mass of the object and a as the rotation parameter).
Now, one chooses the Lewis potentials as follows
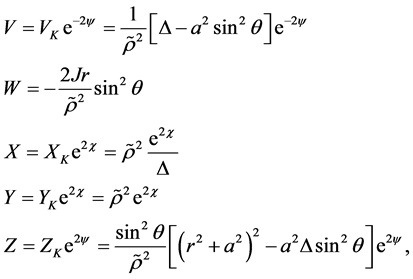 (4)
(4)
where![]() . The potentials
. The potentials ![]() are the Lewis potentials for the Kerr spacetime, and
are the Lewis potentials for the Kerr spacetime, and ![]()
The cross term potential W is unaltered to preserve the following metric form
![]() (5)
(5)
The so chosen potentials guarantee that one gets the Kerr metric if![]() . The function
. The function ![]() and
and ![]() will be determine approximatively from the EFE.
will be determine approximatively from the EFE.
3. The Approximative Kerr Metric with Quadrupole
Now, we have to solve the EFE perturbatively
![]() (6)
(6)
where ![]() (
(![]() ) are the Einstein tensor components,
) are the Einstein tensor components, ![]() are the Ricci tensor components, and R is the curvature scalar.
are the Ricci tensor components, and R is the curvature scalar.
Terms such as
![]() (7)
(7)
(with![]() ) are neglected. The terms corresponding to the Kerr metric of the Ricci tensor components are also eliminated (see Appendix).
) are neglected. The terms corresponding to the Kerr metric of the Ricci tensor components are also eliminated (see Appendix).
To solve the remaining terms of![]() , let propose the following Ansatz
, let propose the following Ansatz
![]() (8)
(8)
where q represents the quadrupole parameter, and![]() . Substituting this Ansatz into the Ricci tensor components, we get a set of linear equations for these constants
. Substituting this Ansatz into the Ricci tensor components, we get a set of linear equations for these constants![]() , and
, and ![]() (
(![]() ). After solving these linear equations, the constants are
). After solving these linear equations, the constants are
![]() (9)
(9)
From (5), the metric components reads
![]() (10)
(10)
It was checked by means of a REDUCE program that the proposed metric is valid up to the order
![]() .
.
4. Comparison to the Hartle-Thorne Metric
In order to establish if our metric does really represent the gravitational field of an astrophysical object, we should show that it is possible to construct an interior solution, which can appropriately be matched with the exterior solution. For this purpose, we employ the exterior HT spacetime [9] [12] . The HT metric describes the exterior of any slowly and rigidly rotating, stationary and axially symmetric body. It is an approximate solution of vacuum EFE. It has three parameters: mass M, spin J and quadrupole-moment Q. The accuracy of this spacetime is given with up to the second order terms in the body’s angular momentum, and first order in its quadrupole moment. The HT solution is given by
![]() (11)
(11)
with metric components
![]() (12)
(12)
where
![]()
![]()
![]()
![]()
The functions ![]() are associated Legendre polynomials of the second kind
are associated Legendre polynomials of the second kind
![]()
![]()
A Taylor expansion of the metric components (12) up to the second order of J, M and q leads to
![]() (13)
(13)
where we have added the second order terms of the quadrupole moment obtained by Frutos and Soffel [16] .
Now, let us expand in Taylor series the metric components (10) up to the second order of a, J, M and q, the result is
![]() (14)
(14)
Comparing these results with the ones obtained by Frutos and Soffel [16] for the ER metric, we note that both metric are the same if one neglects rotation and changes![]() . Our metric corresponds to a rotating ER spacetime at this level of approximation.
. Our metric corresponds to a rotating ER spacetime at this level of approximation.
To compare our spacetime with the HT metric, we have to find a transformation that converts our metric (14) into the HT one (13). The following transformation converts the Kerr-like truncated metric (14) into the improved HT spacetime (13) changing![]() , at the same level of approximation.
, at the same level of approximation.
![]() (15)
(15)
where
![]() (16)
(16)
The constant are given by
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Since our expanded Kerr-like metric can be transformed to the improved HT spacetime, it is possible to construct an interior metric that could be matched to our exterior spacetime. It can be considered as an improvement of the HT spacetime.
5. Comparison to Other Stationary Metrics
There are many other stationary metrics. We concentrate on the Quevedo-Mashhoon [12] [10] and the Manko-Novikov [13] ones. At first glance, our metrics is not the same as these ones, because the rotational term W (4) has no quadrupole perturbation. To see if these metrics are the same, one has to compare the multipole structure. The Ernst potential for metric (5) is [3]
![]() (17)
(17)
where ![]() and
and ![]() is the twist scalar. To get this scalar, we have to solve the following equation
is the twist scalar. To get this scalar, we have to solve the following equation
![]() (18)
(18)
where ![]() is the Killing vector,
is the Killing vector, ![]() is the contravariant derivative and
is the contravariant derivative and
![]() (19)
(19)
Taking the Killing vector as in the Kerr metric![]() . The result of (18) is given by
. The result of (18) is given by
![]() (20)
(20)
This twist is the same as for the Kerr spacetime. Now, the Ernst function is [3]
![]() (21)
(21)
One can show that this Ernst function and its inverse are solutions of the Ernst equation
![]() (22)
(22)
For the sake of calculating the relativistic multipole moments, it is better to employ the inverse function [17] . Moreover, it is easier to calculate them using prolate spheroidal coordinates![]() . The transformation to these coordinates is achieved by means of
. The transformation to these coordinates is achieved by means of
![]() (23)
(23)
where![]() .
.
The potential![]() , the twist scalar
, the twist scalar ![]() and the potential
and the potential ![]() are
are
![]() (24)
(24)
where![]() .
.
The procedure to get the relativistic multipole moments is the following [17] :
1) employ the inverse Ernst potential![]() ,
,
2) set ![]() into
into![]() ,
,
3) change ![]() into
into![]() ,
,
4) expand in Taylor series of z the inverse Ernst potential, and finally,
5) use the Fodor-Hoenselaers-Perjés (FHP) formulae [17] .
To obtain the multipole moment, we wrote a REDUCE program with the latter recipe. The first six mass and first five spin moments are
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
A direct comparison of these multipole moments with the corresponding ones of QM [10] [18] and MN [13] gives that the octupole ![]() is different. Then, all these spacetimes are non-isometric. Moreover, it is clear that the only difference with the Kerr metric is that our metric has another term in the quadrupole moment.
is different. Then, all these spacetimes are non-isometric. Moreover, it is clear that the only difference with the Kerr metric is that our metric has another term in the quadrupole moment.
6. Conclusions
Our metric was obtained solving the EFE perturbatively. The Lewis metric with the modified potentials from the Kerr spacetime was used. This metric has three parameters m, a and q representing the mass, the rotation parameter and the quadrupole, respectively. It is valid until including ![]() and
and ![]() orders. This spacetime contains the Kerr metric, the expanded ER spacetime and an improvement of the HT metric, since as we have seen our expanded version correspond to a HT-like expanded spacetime until including
orders. This spacetime contains the Kerr metric, the expanded ER spacetime and an improvement of the HT metric, since as we have seen our expanded version correspond to a HT-like expanded spacetime until including![]() ,
, ![]() , and
, and ![]() orders.
orders.
The form of our expanded metric suggests that it is possible to construct an interior solution, because it can be transformed to the improved HT spacetime. It is known that the approximate exterior HT metric is coupled to the interior HT one. This gives meaning to our results. Our spacetime may represent the approximative spacetime of a rotating deformed object. Moreover, we improved the HT metric including the second order of the quadrupole moment accuracy. Furthermore, it seems that by means of our perturbation procedure, one could improve our metric to include more terms to a desirable accuracy.
Moreover, the relativistic multipole moments were calculated to show that our spacetime was not isometric with the QM and the MN metrics. Our metric has a simple form and its multipole structure is Kerr-like, the only difference is that it has mass quadrupole.
This metric has potentially many applications because it could be employed as spacetime for real rotating astrophysical objects in a simple manner. Besides, it is easier to implement computer programs to apply this metric, because it maintains the simpleness of the Kerr metric. As an example of possible applications, the influence of the quadrupole moment in the light propagation and the light cone structure of this spacetime could be investigated using this Kerr-like spacetime.
Acknowledgements
We thank the Editor and the referee for their comments. Research of F. Frutos-Alfaro is funded by The Research Vice-Rectory of the University of Costa Rica. This support is greatly appreciated.
Appendix
The non-null Ricci tensor components for the metric (5) (here ![]() do not have the subscript
do not have the subscript ![]() and
and ![]() refers to the Ricci tensor components of the Kerr metric) are given by
refers to the Ricci tensor components of the Kerr metric) are given by
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/ Or contact ijaa@scirp.org