The Influence of Pico-Second Pulse Electron Irradiation on the Electrical-Physical Properties of Silicon Crystals ()
Received 20 June 2016; accepted 5 August 2016; published 8 August 2016

1. Introduction
There are numerous publications devoted to the influence of irradiations, in particular high energy electron irradiation, on the properties of silicon crystal. One can present an extensive bibliography, however it is better to refer to reviews and monographs presenting more informative data about findings on this subject [1] - [5] . The irradiation sources used in these works are conventional sources based on micro-second pulse beams (accelerators, nuclear reactors and so on) allowing to accumulate a large amount of irradiation doses in a short time and, consequently, quickly affect properties of irradiated materials. Not into details of discussing the type and energy of irradiation, it is important to note, though, that at the same irradiation dose, the irradiation intensity (amount of particles per 1 sec. on 1 cm2 cross-section of beam) was proved to play an important role in affecting the properties of semiconductors [6] - [8] .
The case, when the irradiation source has a beam with a pulse shorter than “microsecond”, is important, because it is scientific and practice interest (pulse nuclear reactors, space particle interactions, atmospheric pro- cesses, etc.). For the first time very short pulses with pico-second duration (4 × 10−13 sec.) and electron beam with 3.5 MeV energy was applied which also has scientific meaning for the study of very fast processes in-situ, e.g. interaction of irradiation with material, different chemical and biological reactions. For understanding the pico-second pulse beam influence on the materials, it is better to describe known steps and time intervals of radiation interactions which take place at common “microsecond” irradiation with materials.
2. Problem Formulation and Time Characteristics of Radiation Interaction with Matter
The processes which take place in materials under irradiation can be roughly presented as a raw of consequent stages. The precise duration of each stage depends on initial energy and mass of high energy particle or gamma-quanta, potential of interaction between particles, and can vary an order of magnitude, hence, it is important to estimate the time intervals separating these steps.
The first stage of radiation influence is ionization and excitation of atomic orbital electrons or elastic transfer of irradiation energy to the atoms; the collision time with atoms is estimated to be 10−16 - 10−15 second [2] . Atoms and electrons with excessive energy and impulse come into interaction with other atoms and electrons of matter, loosing energy through this action. This stage is called “energy exchange” from primary exciting particle and transition of the system to quasi-equilibrium state. The energy exchange corresponds to the value of coupling energy of atoms in matter, i.e. a few eV, and takes place very quickly. At the inter-atomic distances this time is about 10−14 - 10−13 second.
The next process, relaxation of excessive energy received by atoms and electrons in crystal, takes place at time which is typical for the period of atomic oscillations, i.e., 10−13 - 10−12 second in solid states. In fact, at this stage relaxation leads the system to the initial state with minimum free energy and to formation of different meta-stable primary radiation defects; the role of thermal movement of atoms in solids becomes significant.
Further consideration relates to processes at average-statistic kinetic energy in order of kТ (k-Bolzman’s constant, T-absolute temperature). The system which is excited by irradiation passes through different quasi-equili- brium states and reconstruction of primary radiation defects occur. The speed of the latter exponentially depends on temperature and can extend over time. Secondary radiation defects are formed which are stable at room temperatures. In their formation both primary radiation defects (vacancies and interstitial atoms) and chemical impurities which were present in samples before irradiation, participate. Diffusion processes and distribution of the components of primary defects over distances play essential role at this stage; this relaxation time duration is estimated by seconds and hours. The formed secondary radiation defects can be “annealed” at high temperatures, but it is not within the scope of present work. Note, that at given pico-second pulse beam irradiation “radiation annealing” which is typical to conventional microsecond pulse beam irradiation, doesn’t take place, because the thermal processes (duration 10−6 - 10−7 second) don’t have enough time to develop.
3. Experimental Procedure and Results
Irradiation of samples was carried out at room temperatures in linear accelerator of САNDLE Synchrotron Radiation Institute (Armenia) by electrons with 3.5 MeV energy, 4 × 10−13 second pulse duration, 12 Hz frequency, charge in impulse was 30 pico-Coulomb. The samples of n-Si were cut out in double-cross shape having 6 Ohmic contacts for electrical measurements, at 0.8 - 1.0 mm thickness, and 3 × 10 mm2 size.
Irradiation dose was defined:
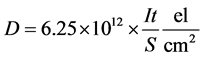 , (1)
, (1)
where I is the mean current in μA, t is exposition time in seconds and S is the cross-section of the beam in cm2.
The beam current was measured by accumulated charge in Faraday cup. Electrical conductivity and charge carriers’ mobility were measured applying known Hall effect method at different temperatures. Electrical conductivity was calculated by σ = mne, where m―charge carriers’ (Hall) mobility, n―concentration of main charge carriers’, e―charge of electron. The charge carriers” mobility was defined by Hall effect measurements:
 , (2)
, (2)
where 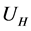 is the potential difference between Hall contacts,
is the potential difference between Hall contacts,  is the potential difference between conductivity contacts, B―magnetic field induction, l―sample’s length, b―sample’s width.
is the potential difference between conductivity contacts, B―magnetic field induction, l―sample’s length, b―sample’s width.
The measurement results are presented in Figures 1-7 as a graphics of dose and temperature dependencies of electrical conductivity and charge carriers’ mobility for samples of different specific resistivity. An obvious “critical dose” is seen on Figure 1, after which the electrical conductivity of samples smoothly decreases and then sharply falls down. This effect depends on their initial specific resistivity, i.e. when the specific resistivity is high the “critical dose” is reached rapidly, so the dependence is inverse to specific resistivity. The charge carrier mobility has similar dependence (Figure 2). Note that for samples with specific resistivity 100 Ω∙cm and 700 Ω∙cm this dependence is almost the same; even in numerical values this dependence is only slightly different, in spite of significant difference in initial carrier concentrations. For samples with specific resistivity 950 Ω∙cm and 700 Ω∙cm the difference in carrier concentration is not so high but there is a significant difference in dose dependences. From comparison of Figure 1 and Figure 2 it is obvious that point radiation defects accumulation kinetics has a marked influence on the mechanism of charge carriers scattering. Note that these measurements were carried out at room temperatures.
Temperature dependencies of electrical conductivity and carrier mobility were studied to clarify the physical nature of their variations after irradiation (Figures 3-7). The carrier mobility measurement results at the 120 - 300 K temperatures for samples with specific resistivity100 Ω∙cm are presented in Figure 3. It is obvious that the behavior of carriers’ mobility temperature dependence before and after irradiation is almost the same up to maximum applied irradiation dose of 6 × 1013 el/cm2.
![]()
Figure 1. Silicon crystal (n-Si) electrical conductivity dose dependence by electron pico-second beam irradiation (energy 3.5 MeV). Samples specific resistivity: 1―100 Ω∙cm, 2―700 Ω∙cm, 3―950 Ω∙cm. Maximum irradiation dose was 6 × 1013 el/cm2.
![]()
Figure 2. Silicon crystal (n-Si) charge carrier’s mobility dose dependence by electron pico-second beam irradiation (energy 3.5 MeV). Samples specific resistivity: 1―100 Ω∙cm, 2―700 Ω∙cm, 3―950 Ω∙cm. Maximum irradiation dose was 6 × 1013 el/cm2.
![]()
Figure 3. Silicon crystal (n-Si) charge carriers’ mobility temperature dependence after electron pico-second beam irradiation (energy 3.5 MeV). Sample specific resistivity100 Ω∙cm: 1―before irradiation, 2―after irradiation by dose 6 × 1013 el/cm2.
However, detailed study of carriers’ mobility temperature dependence in log-log scale points to a difference between these dependences (Figure 4). Almost a straight line over entire temperature interval (line 1) before irradiation indicates the existence of uniform mechanism for carriers’ scattering-scattering on the ionized impurity
![]()
Figure 4. Silicon crystal (n-Si) charge carriers’ mobility temperature dependence after electron pico-second beam irradiation (energy 3.5 MeV). Sample specific resistivity 100 Ω∙cm: 1―before irradiation, 2―after irradiation by dose 6 × 1013 el/cm2. The graphs are in log-log scale for better demonstration. The mathematical expression m~Тa gives possibility to explain charge carriers scattering mechanism for a1 = −2.18 before irradiation and a2 = −1.55; a3 = −1.35 after irradiation. Such behavior of carriers’ mobility (line 2) is explained by carriers’ scattering on the lattice defects.
![]()
Figure 5. Silicon crystal (n-Si) electrical conductivity temperature dependence after electron pico-second beam irradiation (energy 3.5 MeV). Sample specific resistivity is 100 Ω∙cm,: 1―before irradiation, 2―after irradiation by 6 × 1013 el/cm2 dose.
![]()
Figure 6. Silicon crystal (n-Si) charge carriers’ mobility temperature dependence after electron pico-second beam irradiation (energy 3.5 MeV). Samples specific resistivity: 100 Ω∙cm, 1―before irradiation, 4―after irradiation by dose 6 × 1013 el/cm2; 700 Ω∙cm, 2―before irradiation, 5―after irradiation by dose 6 × 1013 el/cm2; 950 Ω∙cm, 3―before irradiation, 6―after irradiation by dose 1.2 × 1013 el/cm2.
![]()
Figure 7. Silicon crystal (n-Si) electrical conductivity temperature dependence after electron pico-second beam irradiation (energy 3.5 MeV). Samples specific resistivity: 100 Ω∙cm, 1―before irradiation, 4―after irradiation by 6 × 1013 el/cm2 dose; 700 Ω∙cm, 2―before irradiation, 5―after irradiation by dose 6 × 1013 el/cm2; 950 Ω∙cm, 3―before irradiation, 6―after irradiation by 1.2 × 1013 el/cm2 dose.
of phosphorus in n-Si. After irradiation there are two mechanisms for carrier scattering (line 2). The mathematical expression for the mentioned cases is as follows: m~Тa, a1 = −2.18 before irradiation and a2 = −1.55; a3 = −1.35 after irradiation. Such behavior of carriers’ mobility (line 2) is explained by carriers’ scattering on the lattice defects [5] ; in the given case, scattering on the radiation defects created by pico-second pulse irradiation with 3.5 MeV energy. Evidence for this statement is temperature dependencies of electrical conductivity and carrier mobility for different samples with specific resistivity of 100 Ω∙cm, 700 Ω∙cm, 950 Ω∙cm (Figure 5 and Figure 6). Samples with specific resistivity of 700 Ω∙cm and 950 Ω∙cm (curves 5 and 6; Figure 6) have an interesting behavior: the constancy of mobility with temperature variation and different temperature dependence of electrical conductivity (Figure 7). This point requires additional comprehensive study.
It is worth mentioning that the behavior of samples with low specific resistivity (i.e. having high impurity concentration) is significantly different from others at low temperatures, where the region of scattering on ionized impurities seen; whereas in samples with high specific resistivity, this region is not observed, although the measurements are difficult at these temperatures because the conductivity is near intrinsic (Figure 7). The primary defect capture by different centers, that were present in samples before irradiation play an important role during these processes [8] . However, at sufficiently high doses (“critical dose”) these channels may be exhausted , i.e. the centers saturated, but, on the other hand, concurrent radiation defects are accumulated, acting as channels for new reactions, leading to the changes of secondary radiation defects spectrum with irradiation dose, other conditions being equal. Along with this, the charge state of formed radiation defects changes, consequently the electrical-physical properties of the crystal also change.
4. Conclusions
From the above given results, the following conclusions can be drawn:
1) In spite of low intensity, pico-second electron irradiation has a significant effect on the electrical-physical properties of silicon crystal.
2) The analysis of measurements shows that stable at room temperatures radiation defect formation in silicon crystal takes place in stages; at first phase defects are formed as vacancy and interstitial atoms which subsequently gather into clusters, although cluster formation is difficult in Si crystal at 3.5 MeV electron energy.
3) Study of temperature dependence of charge carrier mobility helped to reveal their scattering mechanism: scattering on the ionized impurities and on the radiation defects. At the same time it became possible to observe formation of point defects, followed by their cluster formation.
4) The influence of pico-second electron beam irradiation on the silicon crystal with different specific resistivity was studied. It was shown that the “critical dose” corresponding to sharp changes of electrical-physical properties depends on specific resistivity. In these cases it is found to be more appropriate to use an expression “dose threshold” of cluster formation instead of the more commonly used “energy threshold”.
Acknowledgements
This work was supported by the State Committee of Science MES Republic of Armenia in frame of the research project grant NO. 14AR-1c02.
NOTES
![]()
*Corresponding author.