Discrete-Time Dynamic Image Segmentation Using Oscillators with Adaptive Coupling ()
Received 1 June 2016; accepted 25 June 2016; published 28 June 2016

1. Introduction
Image segmentation is one of the most important techniques used in image processing. Many studies have addressed methods of improving the accuracy and effectiveness of image segmentation using various approaches [1] - [3] . An approach uses oscillatory responses from numerical models of coupled oscillators. These are dynamical systems described by differential or difference equations. This approach has been successfully applied to image segmentation. In the locally excitatory globally inhibitory oscillator network model proposed by [4] [5] , coupled oscillators are represented by ordinary differential equations. This method effectively segments input images into image regions [6] [7] . However, these continuous dynamical systems must be integrated over time to produce oscillation, which requires considerable computation time and introduces approximation errors in a numerical simulation.
To address these problems, discrete-time dynamical systems are used as an alternative approach for simulating coupled oscillators. Zhao et al. proposed a model that used a network of coupled logistic maps to achieve multi scale image segmentation [8] . Their model can segment image regions into several clusters based on pixel values. However, because their approach was based on pixel clustering, isolated regions with similar pixel values were assigned to the same cluster.
In contrast with these methods, we previously proposed a discrete-time coupled model that can generate oscillatory responses via periodic points with a high periodic order [9] [10] . This image segmentation system, which we named “dynamic image segmentation system”, uses the synchronized phenomena observed in oscillatory responses in the coupled model. The system was able to segment image regions with similar pixel values, while generating output images in time series.
Our system has a network structure in which two-dimensional (2D) oscillators, based on chaotic neurons [11] [12] , are connected to their four neighboring oscillators and to a global oscillator. The global coupled oscillator makes it possible to distinguish isolated regions with similar pixel values. In the coupled model, each 2D oscillator corresponds to a pixel in the input image. Since each 2D oscillator has two internal state variables, the dynamic image segmentation system for an input image of N pixels is represented by a (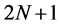 )-dimensional discrete-time coupled model. The lower-dimensional discrete-time coupled model is expected to handle input images comprising a large number of pixels with a faster computational speed. Furthermore, a lower-dimensional coupled model facilitates the addition of functions for adaptive coupling, which allows the dynamic image segmentation of a gray-level image in which the pixel values change gradually.
)-dimensional discrete-time coupled model. The lower-dimensional discrete-time coupled model is expected to handle input images comprising a large number of pixels with a faster computational speed. Furthermore, a lower-dimensional coupled model facilitates the addition of functions for adaptive coupling, which allows the dynamic image segmentation of a gray-level image in which the pixel values change gradually.
In this study, we investigated a novel discrete-time coupled model comprising one-dimensional oscillators based on the Rulkov map [13] and a globally coupled oscillator. The coupled model had 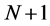 dimensions and a network structure similar to that of the dynamic image segmentation system proposed in our previous studies [14] - [16] . The new model used adaptive coupling to extract image regions in which the pixel values change gradually. Lower-dimensional oscillators were applied to the coupled model, making coupling adaptive. Simulation results demonstrated that our proposed dynamic image segmentation system worked well for gray-level images.
dimensions and a network structure similar to that of the dynamic image segmentation system proposed in our previous studies [14] - [16] . The new model used adaptive coupling to extract image regions in which the pixel values change gradually. Lower-dimensional oscillators were applied to the coupled model, making coupling adaptive. Simulation results demonstrated that our proposed dynamic image segmentation system worked well for gray-level images.
2. Proposed System
In this section, we present the architecture of our proposed discrete-time coupled model with adaptive coupling.
2.1. Discrete-Time Coupled Model
Figure 1 shows the architecture of the coupled oscillator model for dynamic image segmentation [10] . The mechanism of dynamic image segmentation is shown in Figure 2.
The coupled model comprises a global oscillator and N one-dimensional oscillators, where N denotes the number of pixels in an input image. With the exception of the global oscillator, the one-dimensional oscillators are arranged on the grid so that each corresponds to a pixel. They are connected to the eight neighboring oscillators with similar pixel values. The global oscillator connects all the other oscillators and acts as a relay between them. Oscillators with similar pixel values in the eight-neighborhood connection are coupled together. Figure 2 shows second and third (seventh and eighth) oscillators have neighboring connections. Although the responses of the directly coupled oscillators are synchronized, those of the uncoupled ones are out of phase, being connected to the global oscillator with a specific coupling strength. By associating the output value of the ith oscillator with the ith pixel value at each discrete time, segmented images are output as a time series. The discrete-time coupled models are described as follows:
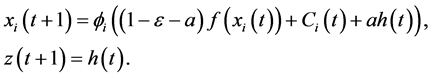 (1)
(1)
Here, 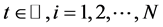 , with
, with  denoting the set of integers, and
denoting the set of integers, and 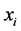 the internal state variable. Functions f and h are described by
the internal state variable. Functions f and h are described by
![]()
Figure 1. Architecture of the coupled oscillators model for dynamic image segmentation.
![]()
Figure 2. Mechanism behind dynamic image segmentation based on oscillatory responses observed in one-dimensional discrete-time oscillators.
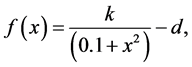 (2)
(2)
and
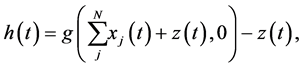 (3)
(3)
where 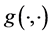 denotes the sigmoid function described by
denotes the sigmoid function described by
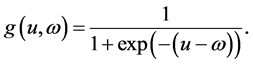 (4)
(4)
Function f is based on the Rulkov map, where h denotes the effect of the global oscillator on each of the other oscillators, and k and d in (2) are tunable system parameters. 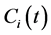 in (1) represents the connection between each oscillator and its eight neighboring oscillators, described by
in (1) represents the connection between each oscillator and its eight neighboring oscillators, described by
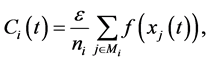 (5)
(5)
where 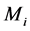 denotes a group of pixels to which the ith pixel connects,
denotes a group of pixels to which the ith pixel connects, ![]() is the number of elements in
is the number of elements in![]() , and
, and ![]() and a in (1) represent the coupling coefficients for the eight neighboring oscillators and the global oscillator, respectively. Finally,
and a in (1) represent the coupling coefficients for the eight neighboring oscillators and the global oscillator, respectively. Finally, ![]() is defined by
is defined by
![]() (6)
(6)
where ![]() is the pixel value of the ith pixel, and
is the pixel value of the ith pixel, and ![]() is an arbitrary threshold. From the function
is an arbitrary threshold. From the function![]() , the oscillator is inhibited when the pixel value is less than
, the oscillator is inhibited when the pixel value is less than![]() .
.
The dynamics of an N-coupled system are described by the P-dimensional discrete-time dynamical system (![]() ) as
) as
![]() (7)
(7)
or, equivalently, by an iterated map defined by
![]() (8)
(8)
where ![]() denotes the set of real numbers. The nonlinear function
denotes the set of real numbers. The nonlinear function ![]() describes the dynamical system of the P-coupled system and is given by
describes the dynamical system of the P-coupled system and is given by
![]() (9)
(9)
where![]() . The three-coupled model shown in Figure 3 is analyzed in detail in Section 4.
. The three-coupled model shown in Figure 3 is analyzed in detail in Section 4.
2.2. Adaptive Coupled Model
The coupling of oscillators defined by (5) is uniformly based on the pixel value of the input image. We replaced this fixed coupling with an adaptive coupling based on the clustering method proposed in [8] . This adaptive coupling was represented as
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
![]()
Figure 3. Architecture of the three-coupled model.
![]() (13)
(13)
![]() (14)
(14)
where ![]() is the pixel value of the ith pixel at iteration t,
is the pixel value of the ith pixel at iteration t, ![]() represents the initial value of the ith pixel,
represents the initial value of the ith pixel, ![]() denotes a group of pixels with
denotes a group of pixels with ![]() around the ith pixel at iteration t,
around the ith pixel at iteration t, ![]() is the number of elements in
is the number of elements in![]() , and the new variables
, and the new variables ![]() and
and ![]() enable each oscillator to adaptively connect to its neighbors.
enable each oscillator to adaptively connect to its neighbors.
3. Analysis
In this section, we describe our analysis, in which we used qualitative bifurcation theory and the order parameter. Note that these analyses must be used to determine the optimum system parameters for dynamic image segmentation, but do not need to be applied every time an image is input.
3.1. Bifurcation Analysis
In our bifurcation analysis, the point ![]() satisfying
satisfying
![]() (15)
(15)
becomes a fixed point of ![]() in (9). If
in (9). If ![]() is a fixed point of
is a fixed point of![]() , the characteristic equation for fixed point
, the characteristic equation for fixed point ![]() is
is
![]() (16)
(16)
where ![]() is the
is the ![]() identity matrix and
identity matrix and ![]() denotes the derivative of
denotes the derivative of![]() . We consider
. We consider ![]() to be hyperbolic if none of the absolute eigenvalues of
to be hyperbolic if none of the absolute eigenvalues of ![]() are at unity. Note that an m-periodic point can be investigated by replacing
are at unity. Note that an m-periodic point can be investigated by replacing ![]() with
with![]() , i.e., the mth iteration of
, i.e., the mth iteration of![]() , in (15). In the following discussion, we consider only the properties of a fixed point of
, in (15). In the following discussion, we consider only the properties of a fixed point of![]() , though a similar argument can be applied to a periodic point of
, though a similar argument can be applied to a periodic point of![]() .
.
Next, we considered the topological classification of a hyperbolic fixed point. Let ![]() be a hyperbolic fixed point and
be a hyperbolic fixed point and ![]() be the intersection of
be the intersection of ![]() and the direct sum of the generalized eigenspaces of
and the direct sum of the generalized eigenspaces of ![]() corresponding to eigenvalue
corresponding to eigenvalue ![]() such that
such that![]() , and let
, and let![]() . Then, the topological type of a hyperbolic fixed point is determined by
. Then, the topological type of a hyperbolic fixed point is determined by ![]() and the orientation-preserving or reversing property of
and the orientation-preserving or reversing property of![]() . Bifurcation occurs when the topological type of a fixed point is changed by varying a system parameter. The generic co-dimension-one bifurcations are the tangent, period-doubling, and Neimark-Sacker bifurcations. In addition, a D-type branching appears in a system that possesses some symmetric properties as a degenerate case of the tangent bifurcation. These bifurcations are observed when hyperbolicity is destroyed, which corresponds to the critical distribution of the characteristic multiplier
. Bifurcation occurs when the topological type of a fixed point is changed by varying a system parameter. The generic co-dimension-one bifurcations are the tangent, period-doubling, and Neimark-Sacker bifurcations. In addition, a D-type branching appears in a system that possesses some symmetric properties as a degenerate case of the tangent bifurcation. These bifurcations are observed when hyperbolicity is destroyed, which corresponds to the critical distribution of the characteristic multiplier ![]() such that
such that ![]() for tangent bifurcation and D- type branching,
for tangent bifurcation and D- type branching, ![]() for period-doubling bifurcation, and
for period-doubling bifurcation, and ![]() for the Neimark-Sacker bifurcation, where
for the Neimark-Sacker bifurcation, where![]() .
.
Bifurcation sets of a fixed point were computed by solving the simultaneous Equations (15) and (16). For the numerical determination [17] , we used Newton’s method. The Jacobian matrix of the set of equations was derived from the first and second derivatives of map F.
3.2. Local Expansion Rates
To investigate the bifurcation phenomena in (2), we used finite-time Lyapunov exponents in which local expansion rates are defined by
![]() (17)
(17)
Here, ![]() is the derivative of function f in (2).
is the derivative of function f in (2).
3.3. Order Parameter
To investigate the relationship between the coupling coefficients and the phase difference of oscillators (in- phase or out-of-phase), we used the order parameter defined by
![]() (18)
(18)
where ![]() and
and ![]() are arbitrary time steps after sufficient time has passed, T is the time step interval from
are arbitrary time steps after sufficient time has passed, T is the time step interval from ![]() to
to![]() , and
, and ![]() is described by
is described by
![]() (19)
(19)
which represents the phase difference between ![]() and
and![]() . The value of
. The value of ![]() in (18) becomes one when the ith and jth oscillators oscillate in-phase; otherwise, the order parameter converges to a value other than one.
in (18) becomes one when the ith and jth oscillators oscillate in-phase; otherwise, the order parameter converges to a value other than one.
4. Analysis Results
We first investigated the bifurcation of the fixed point observed in a single oscillator defined by (2) with no connections. Next, we analyzed the coupled model corresponding to the input image shown in Figure 3. When the input image comprises a ![]() grid of pixels with two isolated image regions, the dynamic image segmentation of a nine-coupled model should first be analyzed. However, as the oscillators corresponding to black pixels were prevented from oscillating by function
grid of pixels with two isolated image regions, the dynamic image segmentation of a nine-coupled model should first be analyzed. However, as the oscillators corresponding to black pixels were prevented from oscillating by function ![]() in (6), we used the three-coupled model in Figure 3 as the model for analysis. We further assumed that each oscillator corresponded to a white pixel when
in (6), we used the three-coupled model in Figure 3 as the model for analysis. We further assumed that each oscillator corresponded to a white pixel when ![]() was larger than
was larger than ![]() in (6). In the bifurcation diagrams shown in this section, symbols
in (6). In the bifurcation diagrams shown in this section, symbols![]() ,
, ![]() , and
, and ![]() represent tangent bifurcation, period-doubling bifurcation, and D-type branching of the fixed point, respectively, and a stable fixed point is present only in the shaded region.
represent tangent bifurcation, period-doubling bifurcation, and D-type branching of the fixed point, respectively, and a stable fixed point is present only in the shaded region.
4.1. Bifurcation Analysis for a Single Oscillator
Figure 4 presents the bifurcation sets observed in a single oscillator defined by (2) in the (k, d)-plane. In the white region, periodic and non-periodic points can be seen. Figure 5(a) shows the one-dimensional bifurcation diagram, while Figure 5(b) shows the local expansion rate calculated by (17) at ![]() for different values of parameter d. Periodic and non-periodic points appear periodically in Figure 5, with the non-periodic points considered to be chaotic because the local expansion rates are greater than zero. Figure 6(a) and Figure 6(b) show waveforms of the stable 56-periodic point and the chaotic behavior at
for different values of parameter d. Periodic and non-periodic points appear periodically in Figure 5, with the non-periodic points considered to be chaotic because the local expansion rates are greater than zero. Figure 6(a) and Figure 6(b) show waveforms of the stable 56-periodic point and the chaotic behavior at ![]() and
and![]() , respectively. Based on these results, we set the system parameters of our coupled model to
, respectively. Based on these results, we set the system parameters of our coupled model to ![]() and
and![]() .
.
4.2. Bifurcation Analysis of the Three-Coupled Model
Figure 7 plots the bifurcation sets of the three-coupled model in the (a, e)-plane. At the right-hand region of curve![]() , a high order of periodic and non-periodic points is observed. In the non-shaded left-hand region of curve
, a high order of periodic and non-periodic points is observed. In the non-shaded left-hand region of curve![]() , non-periodic points with small amplitudes can be seen. Bifurcation analysis suggested that oscillatory responses appropriate to segmentation of a large image was dependent on the coefficients of coupling. Based on these results, we set parameters a and e to 0.001 and 1.0, respectively.
, non-periodic points with small amplitudes can be seen. Bifurcation analysis suggested that oscillatory responses appropriate to segmentation of a large image was dependent on the coefficients of coupling. Based on these results, we set parameters a and e to 0.001 and 1.0, respectively.
4.3. Results of Analysis by Order Parameter for Three-Coupled Model
Figure 8 shows the relationship between the order parameters calculated by (18) and the coupling coefficients
![]()
Figure 4. Bifurcation diagram of a fixed point observed in a single oscillator.
![]()
Figure 5. (a) One-dimensional bifurcation diagram and (b) local expansion rate where![]() .
.
![]()
Figure 6. (a) Periodic and (b) non-periodic points observed in a one-dimensional discrete-time single oscillator with![]() .
.
![]()
Figure 7. Bifurcation diagram of a fixed point observed in the three-coupled model.
with![]() ,
, ![]() , and
, and![]() . Figure 8(a) and Figure 8(b) show
. Figure 8(a) and Figure 8(b) show ![]() and
and ![]() calculated at different values of parameter
calculated at different values of parameter ![]() and
and![]() . As shown in Figure 8(a),
. As shown in Figure 8(a), ![]() remained at one in the range of
remained at one in the range of ![]() approximately from zero to one, and was otherwise less than one. Figure 8(b) shows that
approximately from zero to one, and was otherwise less than one. Figure 8(b) shows that ![]() was less than one in the range of
was less than one in the range of ![]() from −0.2 to 1.2. These results demonstrate that the first and second oscillators were in-phase in the range approximately from zero to one of
from −0.2 to 1.2. These results demonstrate that the first and second oscillators were in-phase in the range approximately from zero to one of![]() , whereas the first and third oscillators were out-of-phase under the given parameters. Figure 8(c) and Figure 8(d) show the relationship between the order parameters and parameter a at
, whereas the first and third oscillators were out-of-phase under the given parameters. Figure 8(c) and Figure 8(d) show the relationship between the order parameters and parameter a at![]() . Figure 8(c) shows that, whereas parameter a changed,
. Figure 8(c) shows that, whereas parameter a changed, ![]() remained at one, suggesting that the first and second oscillators were in-phase, and had no relation to parameter a. Conversely, the phase between the first and third oscillators periodically changed in response to parameter a, as shown in Figure 8(d). These results suggested that the phase difference between the oscillators corresponding to disconnected
remained at one, suggesting that the first and second oscillators were in-phase, and had no relation to parameter a. Conversely, the phase between the first and third oscillators periodically changed in response to parameter a, as shown in Figure 8(d). These results suggested that the phase difference between the oscillators corresponding to disconnected
![]()
Figure 11. Output images obtained by dynamic image segmentation with adaptive coupling. The number below each image represents the time step in Figure 9.
regions could be controlled by adjusting parameter a.
5. Applying Our Model to Dynamic Image Segmentation
Simulation were used to demonstrate that dynamic image segmentation could be achieved using our adaptive coupled model with appropriate parameter values. The parameter values were set as follows:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and![]() . Figure 9 shows the three-phase oscillatory response observed in a
. Figure 9 shows the three-phase oscillatory response observed in a ![]() -coupled model with adaptive coupling corresponding to the input image shown in Figure 10. The image had three isolated regions in which the pixel values changed gradually from white to gray. Our simulation produced the output images shown in Figure 11. These results demonstrated the ability of our proposed adaptive coupling model to segment gray-level images with gradually changing pixel values.
-coupled model with adaptive coupling corresponding to the input image shown in Figure 10. The image had three isolated regions in which the pixel values changed gradually from white to gray. Our simulation produced the output images shown in Figure 11. These results demonstrated the ability of our proposed adaptive coupling model to segment gray-level images with gradually changing pixel values.
6. Conclusion
In this study, we proposed a novel discrete-time coupled model for use in dynamic image segmentation. The mechanisms underlying the generation of oscillatory responses in a single oscillator were revealed by a bifurcation analysis. We also investigated the bifurcation sets for the fixed point observed in a three-coupled model. Using order parameters to show the phase differences between the oscillators, we elucidated the relationship between the oscillatory responses and the coupling coefficients of oscillators in the three-coupled model. We used this bifurcation analysis to set appropriate parameter values and applied our model to dynamic image segmentation. Data from simulations demonstrate that our proposed model is capable of segmenting regions of a gray-level image in which the pixel values change gradually. In future work, we will analyze our proposed model in greater detail, for example, by applying it to input images with more isolated image regions.