Received 31 January 2016; accepted 23 February 2016; published 26 February 2016

1. Introduction
In general, to any problem stated in the form of a maximization (minimization) criterion, there corresponds a dual specification in the form of a minimization (maximization) goal. This structure applies also to the Maximum Likelihood (ML) approach, one of the most widely used statistical methodologies. A clear description of the Maximum Likelihood principle is found in Kmenta ([1] , p. 175-180): Given a sample of observations about random variables, “the question is: To which population does the sample most likely belong?” The answer can be found by defining ( [2] p. 396) “the likelihood function as the joint probability distribution of the data, treated as a function of the unknown coefficients. The Maximum Likelihood (ML) estimator of the unknown coefficients consists of the values of the coefficients that maximize the likelihood function”. That is, the maximum likelihood estimator selects the parameter values that give the observed data sample the largest possible probability of having been drawn from a population defined by the estimated coefficients.
In this paper, we concentrate on data samples drawn from normal populations and deal with linear statistical models. The ML approach, then, estimates the mean and variance of that normal population that will maximizes the likelihood function given the sample information.
The novel contribution of the paper consists in developing the dual specification of the Maximum Likelihood method (under normality) and in giving it an intuitive economic interpretation that corresponds to the maximization of the net value of sample information. The dual specification is of interest because it exists and integrates the knowledge of the Maximum Likelihood methodology. In fact, to any maximization problem subject to linear constraints there corresponds a minimization problem subject to some other type of constraints. The two specifications are equivalent in the sense that they provide identical values of the parameter estimates, but the two paths to achieve those estimates are significantly different. In mathematics, there are many examples of how the same objective (solutions and parameter estimates) may be achieved by different methods. This abundance of approaches has often inspired further discoveries.
The notion of the dual specification of a statistical problem is not likely familiar to a wide audience of statisticians in spite of the fact that a large body of statistical methodology relies explicitly on the maximization of a likelihood function and the minimization of a least-squares function. These optimizations are simply primal versions of statistical problems. Yet, the dual specification of the same problems exists in an analogous manner as the back face of the moon exists and was unknown until a spacecraft circumnavigated that celestial body. Hence, the dual specification of the ML methodology enriches the statistician’s toolkit and understanding of the methodology.
The analytical framework that ties together the primal and dual specifications of a ML problem is the Lagrange function. This important function has the shape of a saddle where the equilibrium point is achieved by maximizing it in one direction (operating with primal variables: parameters and errors) and minimizing it in the other, orthogonal direction (operating with dual variables: Lagrange multipliers). Lagrange multipliers and their meaning, therefore, are crucial elements for understanding the structure of a dual specification.
In Section 2, we present the traditional Maximum Likelihood method in the form of a primal nonlinear programming model. This specification is a natural step toward the discovery of the dual structure of the ML method. It differs from the traditional way to present the ML approach because the model equations (representing the sample information) are not substituted into the likelihood function but are stated as constraints. Hence, the estimates of parameters and errors of the model are computed simultaneously rather than sequentially. A remarkable result of this setup is that the Lagrange multipliers associated with the linear statistical model (regarded as a set of constraints defined by the sample observations) are revealed to be equal to the residuals scaled by the variance of the error terms. Section 3 derives and interprets the dual specification of the ML method. The intuitive interpretation of the dual problem appeals to basic elements of information theory and economics. The economic interpretation of Lagrange multipliers as shadow prices (prices that cannot be seen on the market) establishes that the dual ML minimizes the negative net value of sample information (NVSI), which is equivalent to maximize the NVSI. This economic notion will be clarified further in subsequent sections. Although the numerical solution of the dual ML method is feasible (as illustrated with a non trivial numerical example in Section 4), the main goal of this paper is to present and interpret the dual specification of the ML method as integrating the understanding of the double role played by residuals. It turns out that residual errors in the primal model assume the intuitive role of noise while, in the dual model, they assume the intuitive role of penalty parameters (for violating the constraints) that in economics correspond to the notion of “marginal sacrifices” or “shadow prices”. The name “marginal sacrifices” indicates that the size of Lagrange multipliers represents a measure of constraint’s tightness (in this case, of the observations in the linear model) and influences directly the value of the likelihood function. In other words, the optimal value of the likelihood function varies precisely according to the value of the Lagrange multiplier per unit increase (or decrease) in the level of the associated observation. In this sense, in economics it is customary to refer to the level of a Lagrange multiplier as the “marginal sacrifice” (or “shadow price”) due to the active presence of the corresponding constraint that limits the increase or decrease of the objective function.
Section 4 presents a numerical example where the parameters of a linear statistical model are estimated using the dual ML specification. The sample size is composed of 114 observations and there are six parameters to be estimated. A peculiar feature of this dual estimation is given by the analytical expression of the model variance that must use a rarely recognized formula.
2. The Primal of the Maximum Likelihood Method (Normal Distribution)
We consider a linear statistical model
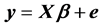 (1)
(1)
where  is an
is an 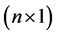 vector of sample data (observations),
vector of sample data (observations), 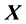 is an
is an 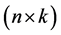 matrix of predetermined values of explanatory variables,
matrix of predetermined values of explanatory variables, 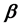 is a
is a 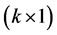 vector of unknown parameters, and
vector of unknown parameters, and 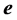 is an
is an 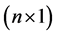 vector of random errors that are assumed to be independently and normally distributed as
vector of random errors that are assumed to be independently and normally distributed as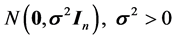 . The vector of observations
. The vector of observations 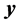 is known also as the sample information. Then, ML estimates of the parameters and errors can be obtained by maximizing the logarithm of the corresponding likelihood function with respect to
is known also as the sample information. Then, ML estimates of the parameters and errors can be obtained by maximizing the logarithm of the corresponding likelihood function with respect to 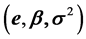 subject to the constraints represented by model (1). We call this specification the primal ML method. Specifically,
subject to the constraints represented by model (1). We call this specification the primal ML method. Specifically,
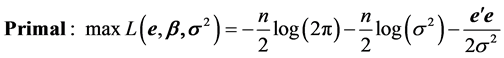 (2)
(2)
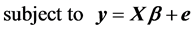 (3)
(3)
Traditionally, constraints (3) are substituted for the error vector 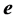 in the likelihood function (2) and an unconstrained maximization calculation will follow. This algebraic manipulation, however, obscures the path toward a dual specification of the problem under study. Therefore, we maintain the structure of the ML model as in relations (2) and (3) and proceed to state the corresponding Lagrange function by selecting a
in the likelihood function (2) and an unconstrained maximization calculation will follow. This algebraic manipulation, however, obscures the path toward a dual specification of the problem under study. Therefore, we maintain the structure of the ML model as in relations (2) and (3) and proceed to state the corresponding Lagrange function by selecting a ![]() vector
vector ![]() of Lagrange multipliers of constraints (3) to obtain
of Lagrange multipliers of constraints (3) to obtain
![]() (4)
(4)
The maximization of the Lagrange function (4) requires taking partial derivatives of ![]() with respect to
with respect to![]() , setting them equal to zero, in which case we signify that a solution of the resulting equations is an estimate of the corresponding parameters and errors:
, setting them equal to zero, in which case we signify that a solution of the resulting equations is an estimate of the corresponding parameters and errors:
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
First order necessary conditions (FONC) are given by equating (5)-(8) to zero and signifying by “^” that the resulting solution values are ML estimates. We obtain
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
where![]() . Lagrange multipliers
. Lagrange multipliers ![]() are defined in terms of the estimates of primal variables
are defined in terms of the estimates of primal variables ![]() and
and![]() . Indeed, the vector of Lagrange multipliers
. Indeed, the vector of Lagrange multipliers ![]() is equal to
is equal to ![]() up to a scalar
up to a scalar![]() . This equality simplifies the statement of the corresponding dual problem because we can dispense with the symbol
. This equality simplifies the statement of the corresponding dual problem because we can dispense with the symbol![]() . In fact, using Equation (9), Equation (10) can be restated equivalently as the following orthogonality condition between the residuals of model (1) and the space of predetermined variables
. In fact, using Equation (9), Equation (10) can be restated equivalently as the following orthogonality condition between the residuals of model (1) and the space of predetermined variables
![]() (13)
(13)
Relation (9) is an example of self-duality where a vector of dual variables is equal (up to a scalar) to a vector of primal variables.
The value of a Lagrange multiplier is a measure of tightness of the corresponding constraint. In other words, the optimal value of the likelihood function would be modified in the amount equal to the value of the Lagrange multiplier per unit value increase (or decrease) in the level of the corresponding sample observation. The meaning of a Lagrange multiplier (or dual variable) is that of a penalty imposed on a violation of the corresponding constraint. Hence, in the economic terminology, a synonymous meaning of the Lagrange multiplier is that of a “marginal sacrifice” (or “shadow price”) associated with the presence of a tight constraint (observation) that prevents the objective function to achieve a higher (or lower) level. Within the context of this paper, the vector of optimal values of the Lagrange multipliers ![]() is identically equal to the vector of residuals
is identically equal to the vector of residuals ![]() scaled by
scaled by![]() . Therefore, the symbol
. Therefore, the symbol ![]() takes on a double role: as a vector of residuals (or noise) in the primal ML problem [(2)-(3)] and―when scaled by
takes on a double role: as a vector of residuals (or noise) in the primal ML problem [(2)-(3)] and―when scaled by![]() ―as a vector of “shadow prices” in the dual ML problem (defined in the next section).
―as a vector of “shadow prices” in the dual ML problem (defined in the next section).
Furthermore, note that the multiplication of Equation (12) by the vector ![]() (replaced by its equivalent representation given in Equation (9)) and the use of the orthogonality condition (13) produces
(replaced by its equivalent representation given in Equation (9)) and the use of the orthogonality condition (13) produces
![]() (14a)
(14a)
![]() (14b)
(14b)
![]() (14c)
(14c)
This means that a ML estimate of ![]() can be obtained in two different but equivalent ways as
can be obtained in two different but equivalent ways as
![]() (15)
(15)
Relation (15), as explained in sections 3 and 4, is of paramount importance for stating an operational specification of the dual ML model because the presence of the vector of sample observations ![]() in the estimate of
in the estimate of ![]() is the only place where this sample information appears in the dual ML model. This assertion will be clarified further in Sections 3 and 4.
is the only place where this sample information appears in the dual ML model. This assertion will be clarified further in Sections 3 and 4.
3. The Dual of the Maximum Likelihood Method
The statement of the dual specification of the ML approach follows the general rules of duality theory in mathematical programming. The dual objective function, to be minimized with respect to the Lagrange multipliers, is the Lagrange function stated in (4) with the appropriate simplifications allowed by its algebraic structure and the information derived from FONCs (9) and (10). The dual constraints are all the FONCs that are different from the primal constraints. This leads to the following specification:
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
The second expression of the dual ML function (16) follows from the fact that ![]() (from (15)). The solution of the dual ML problem [(16)-(18)] by any reliable nonlinear programming software (e.g., GAMS, [3] ) produces estimates of
(from (15)). The solution of the dual ML problem [(16)-(18)] by any reliable nonlinear programming software (e.g., GAMS, [3] ) produces estimates of ![]() that are identical to those obtained from the primal ML problem [(2)-(3)]. Observe that the vector of sample information
that are identical to those obtained from the primal ML problem [(2)-(3)]. Observe that the vector of sample information ![]() appears only in Equation (18). This fact justifies the computation of the model variance
appears only in Equation (18). This fact justifies the computation of the model variance ![]() by means of the rarely used formula (18). The dual ML estimate of the parameter vector
by means of the rarely used formula (18). The dual ML estimate of the parameter vector ![]() is obtained as a vector of Lagrange multipliers associated to the orthogonality constraints (17). The terms in the square bracket of the dual objective function (16) express a quantity that has intuitive appeal, that is
is obtained as a vector of Lagrange multipliers associated to the orthogonality constraints (17). The terms in the square bracket of the dual objective function (16) express a quantity that has intuitive appeal, that is
![]() (19)
(19)
Using the terminology of information theory, the expression in the right-hand-side of Equation (19) can be given the following interpretation. The linear statistical model (1) can be regarded as the decomposition of a message into a signal and noise, that is
message = signal + noise (20)
where message![]() , signal
, signal![]() , and noise
, and noise![]() . Let us recall that
. Let us recall that ![]() is the “shadow price” of the constraints of model (1) (defined by (2)) and
is the “shadow price” of the constraints of model (1) (defined by (2)) and ![]() is the quantity of sample information. Hence, the inner product
is the quantity of sample information. Hence, the inner product ![]() can be regarded as the gross value (price times quantity) of the sample information while the expression
can be regarded as the gross value (price times quantity) of the sample information while the expression ![]() (again, shadow price times quantity) can be regarded as a cost function of noise. In summary, therefore, the relation
(again, shadow price times quantity) can be regarded as a cost function of noise. In summary, therefore, the relation ![]() can be interpreted as the net value of sample information (NVSI) that is maximized in the dual objective function because of the negative sign in front of it.
can be interpreted as the net value of sample information (NVSI) that is maximized in the dual objective function because of the negative sign in front of it.
A simplified (for graphical reasons) presentation of the primal and dual objective functions (2) and (16) of the ML problem (subject to constraints) may provide some intuition about the shape of those functions. Figure 1 is the antilog of the primal likelihood function (2) (subject to constraint (3)) of a sample of two random variables ![]() with mean 0 and variance 0.16. The sample information is
with mean 0 and variance 0.16. The sample information is![]() . For graphical reasons, the variance of the error terms is kept fixed at
. For graphical reasons, the variance of the error terms is kept fixed at![]() . The explanatory variables are taken as
. The explanatory variables are taken as![]() . There are two parameters to estimate:
. There are two parameters to estimate: ![]() and
and![]() . The ML estimates of these parameters are
. The ML estimates of these parameters are ![]() and
and ![]() with
with ![]() and
and ![]()
Figure 1 presents the expected shape of the primal likelihood function (subject to constraints) that justifies the maximization objective.
Figure 2 is the antilog of the dual objective function (16) (subject to constraint (17)) for the same values of variables Y and X. Figure 2 shows a convex function of the error terms with ![]() and
and ![]() being the minimizing values of the dual objective function.
being the minimizing values of the dual objective function.
It is well known that, under the assumptions of model (1), least-squares estimates of the parameters of model (1) are also maximum likelihood estimates. Hence, ![]() is the primal objective function (to be minimized) of the least-squares method while
is the primal objective function (to be minimized) of the least-squares method while ![]() corresponds to the dual objective function (to be maximized) of the least-squares approach as in [4] . Optimal solutions of primal and dual least-squares problems result in
corresponds to the dual objective function (to be maximized) of the least-squares approach as in [4] . Optimal solutions of primal and dual least-squares problems result in
![]() (21)
(21)
where LS stands for Least Squares. The role as a vector of “shadow prices” taken on by ![]() is justified also by the derivative of the Least-Squares function with respect to the quantity vector of sample information y. In this case,
is justified also by the derivative of the Least-Squares function with respect to the quantity vector of sample information y. In this case,
![]()
![]()
Figure 1. Representation of the antilog of the primal objective function (2).
![]()
Figure 2. Representation of the antilog of the dual objective function (16).
shows that the change in the Least-Squares objective function due to an infinitesimal change in the level of the quantity vector of constraints ![]() (sample information in model (1)) corresponds to the Lagrange multiplier vector
(sample information in model (1)) corresponds to the Lagrange multiplier vector ![]() that, in the LS case, is equal to the vector of residuals
that, in the LS case, is equal to the vector of residuals![]() .
.
4. A Numerical Example: Parameter Estimates by Primal and Dual ML
In this section we consider the estimation of a production function using the results of a famous experimental trial on corn conducted in Iowa by Heady, Pesek and Brown [5] . There are n = 114 observations on phosphorus and nitrogen levels allocated to corn experimental plots according to an incomplete factorial design. The sample data are given in Table A1 in Appendix. The production function of interest takes the form of a second order polynomial relation involving phosphorus and nitrogen such as
![]() (22)
(22)
where ![]() corn,
corn, ![]() phosphorus and
phosphorus and ![]() nitrogen.
nitrogen.
This polynomial regression was estimated twice: using the primal ML specification given in (2) and (3) and, then, using the dual ML version given in (16), (17) and (18). The results are identical and are reported (only once) in Table 1.
Specifically, the estimated dual ML model takes on the following structure:
![]()
Table 1. ML estimates using the dual specification.
![]() (23)
(23)
![]() (24)
(24)
![]() (25)
(25)
The estimation was performed using GAMS [3] . Observe that the sample information ![]() appears only in Equation (25) that estimates the model variance
appears only in Equation (25) that estimates the model variance![]() . The estimates of parameters
. The estimates of parameters ![]() will appear in the Lagrange function as Lagrange multipliers of constraints (24).
will appear in the Lagrange function as Lagrange multipliers of constraints (24).
5. Conclusions
A statistical model may be regarded as the decomposition of a sample of messages into signals and noise. When the noise is distributed according to a normal density, the ML method maximizes the probability that the sample belongs to a given normal population defined by the ML estimates of the model’s parameters. All this is well known. This paper has analyzed and interpreted the dual of the ML method under normal assumptions.
It turns out that the dual objective function is a convex function of noise. Hence, a convenient interpretation is that the dual of the ML method minimizes a cost function of noise. This cost function is defined by the sample variance of noise. Equivalently, the dual ML method maximizes the net value of the sample information. The choice of an economic terminology for interpreting the dual ML method is justified by the double role played by the symbol ![]() representing the vector of residual terms of the estimated statistical model. This symbol may be interpreted as a vector of noises in the primal specification and a vector of “shadow prices” in the dual model because it corresponds identically (up to a scalar) to the vector of Lagrange multipliers of the sample observations.
representing the vector of residual terms of the estimated statistical model. This symbol may be interpreted as a vector of noises in the primal specification and a vector of “shadow prices” in the dual model because it corresponds identically (up to a scalar) to the vector of Lagrange multipliers of the sample observations.
The numerical implementation of the dual ML method brings to the fore, by necessity, a neglected definition of the sample variance. In the ML estimation of the model’s parameters, it is necessary to state the definition of the variance as the inner product of the sample information and the residuals (noise), as revealed by Equations (15) and (25), because it is the only place where the sample information appears in the dual model. The dual approach to ML provides an alternative path to the desired ML estimates and, therefore, augments the statistician’s toolkit. It integrates our knowledge of what exists on the other side of the ML fence, a territory that has revealed interesting vistas on old statistical landscapes.
Appendix
![]()
Table A1. Sample data from the Iowa corn experiment [5] .