1. Introduction
The improved Boussinesq equation (IBq) was proposed in Bogolyubsky’s work [1] , like a correct modification to solve the bad Boussinesq equation (BBq) which describes a large group of nonlinear dispersive wave phenomena, such as propagation of long waves on the surface of shallow water in both directions, propagation of ion-sound waves in a uniform isotropic plasma, and so on [2] . Bogolyubsky has also shown that the BBq equation describes an unphysical instability of short wave lengths and the Cauchy problem for this partial differential equation is incorrect. The BBq equation was first introduced in the 1870s by Joseph Boussinesq [3] , which is given by
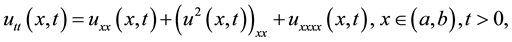(1)
where 
is a sufficiently differentiable real function, the correct modification to this partial dif- ferential equation is given by
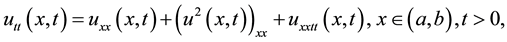(2)
which is the IBq and will be the principal study equation of this paper; it is convenient for computer simulation of the dynamics of different nonlinear waves with weak dispersion; in our case the IBq equation will help to formulate the finite element discretization in the spatial direction with the primal L2-Galerkin finite element formulation [4] [5] ; this due to the correction in the fourth order derivative term which now leads us to the integral of a discontinuous function over a set of measure zero (for the Lagrange finite element
). The IBq (2) has the 1-soliton solution [6] .
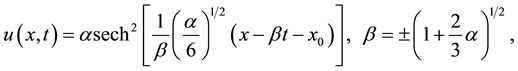(3)
where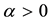
, is the wave amplitude, 
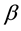is the wave speed and 
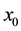is the soliton center of symmetry. The initial displacement and velocity condition to the (2) equation are assumed to have the form.
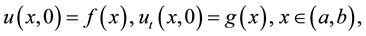(4)
where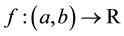 
and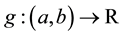 
are given functions in each example.
The boundary conditions at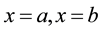 
are assumed to be
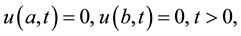(5)
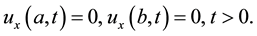(6)
Linearization techniques and finite differences are employed in most numerical works that solve the IBq [7] - [10] ; they need a relevant stability relation between the space and time discretization size, obtained by the Fourier method of analyzing stability and the Von Neumann’s necessary criterion for stability [11] [12] ; in
contrast with the method proposed in this paper such a restriction is not needed. The nonlinear term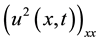 
which for the finite difference method is a problem and needs to be linearized with the help of bounds solutions and/or iterative approach [10] is not a problem in our work which is treated formally by the L2-Galerkin finite element formulation and leads us due to the reduced support in the basis functions to a time dependent tridia- gonal antisymmetric square matrix for the 
Lagrange element case, so the only linearization is inherent to the finite element method; in this way the following Lagrange elements ![]()
are expected to work with
better convergence properties in the x direction. The ![]()
convergence in the proposed method is verified with the standard procedure [13] using ![]()
-norm. Wave propagation, wave break up, inelastic and elastic
head-on collision, and blow-up solution are modeled and graphics representations are done [14] .
2. The Classical Finite Element Method
The classical finite element method relies over two basic ingredients [4] [5] , the first is a weak or variational formulation for the IBq equation which is obtained for a fixed t by multiplying with a test function
![]()
where ![]()
is the standard Sobolev space [15] defined by
![]()
(7)
the subindex and superindex 0, 1 refers to boundary conditions and to the derivative order that should belong to ![]()
respectively, and integrate over ![]()
to get after integrating by parts and applying the boundary conditions (5), the variational formulation for the IBq equation.
Find ![]()
such that for ![]()
![]()
(8)
A classical (or conforming) approximation of u is obtained by looking for a function ![]()
with ![]()
such that
![]()
(9)
The second basic ingredient for the classical finite element method is to choose the finite dimensional subspace![]()
, in our case will be constructed with the finite element ![]()
from the Lagrange family [4] [5] , to
this end let![]()
, be a partition of the interval ![]()
into subintervals ![]()
of length![]()
, in our work a non adaptive mesh will be considered so
![]()
, we now let ![]()
to be the set of functions v such that v is linear on each subinterval ![]()
is continuos on ![]()
and ![]()
As parameters to describe a function ![]()
we may choose the values ![]()
at the node points![]()
. Let us introduce the linear basis functions![]()
, defined by [5]
![]()
In this way for each ![]()
a function ![]()
has the unique representation
![]()
as a linear combination of the basis functions![]()
, and ![]()
is a linear vector space of dimension ![]()
with basis![]()
. The variational problem (9) is equivalent to the follow- ing L2-Galerkin space semi-discretization for the IBq equation. Find ![]()
such that
![]()
(10)
If we substitute ![]()
and take in turn ![]()
in (10) we will obtain a second order in time nonlinear ordinary differential equations system to aproximate ![]()
which in matrix notation is
![]()
(11)
where![]()
, ![]()
are N by N matrices which will be calculated in the next section and as before![]()
.
3. The Finite Element Computational Aspects
As is usual all finite element computations like integration, interpolation are done over the master element ![]()
over ![]()
the following local basis functions are needed to integrate,
![]()
(12)
they have the property ![]()
and ![]()
see Figure 1.
The local finite element matrices are calculated over ![]()
with the help of functions in (12) then multiplied
by the respective scale factor, to get the finite element matrix over![]()
, then we need to do the
![]()
Figure 1. Local basis functions associated to the points -1, +1.
typical finite element assembly to get the global matrices![]()
. For instance the matrix M, using the scale factor ![]()
is constructed from ![]()
in the following way
![]()
transforms to
![]()
and after assembly from element 2 to N, M is given as follows
![]()
over ![]()
and ![]()
the basis functions should satisfy the respective boundary conditions (5), assembling these components to the last M we finally arrived to
![]()
analogously for K whose scale factor for integration is![]()
,
![]()
the matrix ![]()
follows the same steps with scale factor ![]()
![]()
![]()
finally after assembly and putting the boundary conditions
![]()
this matrix represents the nonlinearity in the IBq Equation (2), the anti-symmetry structure is related to the ![]()
Lagrange finite element and to the primal variational formulation and not to nonlinearity.
4. The Initial Value Problem
With the matrices ![]()
and ![]()
at hand it is possible to solve the nonlinear initial value problem (11), to get a unique solution it is necessary to impose the initial conditions (4), the system (11) is equivalent to
![]()
(13)
the matrix ![]()
is a tridiagonal positive definite and therefore invertible [14] , as is usual with second order systems, one should introduce a new vector variable ![]()
in this way the system (13) is equivalent to
the next first order nonlinear system of ordinary differential equations:
![]()
(14)
![]()
(15)
with initial conditions
![]()
(16)
the system (14) and (15), (16) is a standard initial value problem that can now be solved by integration algorithms like predictor corrector [9] [11] and not by simply fourth order Runge-Kutta method. This paper will employ Runge-Kutta-Fehlberg of fourth and fifth order with variable time step size, the fifth order method will work like a predictor and the fourth order like a corrector [16] .
5. Numerical Examples
Firstly in Numerical Validation, the proposed method is used for the numerical wave propagation simulation, and comparing this simulation with the exact solution we validate the method, we are really approximating the soliton solution by a non-classical one, the compacton [17] .
1. Numerical Validation. We set ![]()
and ![]()
![]()
(17)
![]()
(18)
the exact solution is given by (3), we discretize over ![]()
and![]()
, the numerical results
are compared for t = 20 with the exact solution at some points in Table 1, where ![]()
means the numerical solution, and the wave propagation numerical graphic is illustrated by Figure 2 and Figure 3 where the level curves are showed.
2. Wave brake-up. With the same ![]()
as in Numerical Validation, ![]()
and ![]()
we will have an example of wave brake-up propagation, taking ![]()
Figure 4 is plotted with the numerical solution and Figure 5 shows the level curves.
![]()
Table 1. Comparison of numerical and exact solution,![]()
.
![]()
Figure 3. Level curves for soliton propagation.
![]()
Figure 5. Level curves for soliton brake-up.
3. The head-on wave collision. In this example we take ![]()
with ![]()
and ![]()
![]()
(19)
![]()
(20)
A negative speed indicate a wave traveling to the negative x side direction, so the two waves will have a head-on collision [18] . We obtain an inelastic collision, the Figure 6 shows the collision intercourse and Figure 7 the level curves where secondary solitons are visible, hence the collision is inelastic.
![]()
Figure 7. Level curves for inelastic head-on collision.
The next examples are done with different amplitudes![]()
.
If![]()
, the collision is inelastic.
If![]()
, the collision is inelastic.
If![]()
, the collision is elastic.
If![]()
, the collision is still elastic. The Figure 8 and Figure 9 show this case.
These results are in good agreement with those reported elsewhere [1] [8] .
![]()
Figure 9. Level curves for elastic head-on collision.
4. Blow-up solution. The blow-up solution is now simulated as discussed in [19] [20] , the IBq (2) is solved
numerically on ![]()
with 200 finite elements in the x direction and ![]()
with initial conditions given by
![]()
(21)
It is know [19] the existence of ![]()
such that exist unique local solution with ![]()
as ![]()
by the left side and ![]()
as ![]()
by the left side, Figure 10 and Figure 11 show the numerical results for some fixed times between ![]()
and![]()
.
5. Convergence Order. For our technique, the convergence order will be calculated in the usual way using the results from Numerical Validation, as the following Table 2 shows the rate of convergence for Lagrange k = 1 finite element is ![]()
in space.
6. Conclusion
A concrete development of a practical ![]()
finite element scheme is used to make a semi discretization in the x direction and reduce the IBq equation to a system of ordinary differential equation with initial value; this de- velopment open the door to try the next ![]()
Lagrange finite elements to get a better convergence property in the x direction, and the numerical results are highly accurate as Numerical Validation shows. A wave
brake-up result if the initial pulse is steady. The head-on collision is successfully simulated to different wave amplitudes to obtain the existence of a critical value 0.5. If the amplitudes are below or even equal to this critical value, the head-on collision is elastic and the graphics show a clean interaction before and after the collision. If one or two of the amplitudes are greater than the critical value, the head-on collision is inelastic and the graphics show a secondary soliton interaction. It has been verified numericaly the existence of a blow-up solution in finite time to a theoretical problem and was noted that for the ![]()
Lagrange finite elements the trivial boundary conditions should be incorporated with care. A fourth order convergence is verified calculating in the usual way the sucessive quotients errors in the infinity norm [13] . The numerical technic can be implemented using mathematical software where many solvers for the initial value problem are available. The nonlinear term in the IBq does not need a special handle like bounds or iterative procedures; this term led us to a nonlinear time
dependent matrix called ![]()
which at each prediction and correction will change as solution does. The results are in good conformity with those reported by Bogolyubskii [6] .
Acknowledgements
This work was supported in part by the Secretary of Education of Mexico under the project PROMEP 103.5/13/9347 for developing research scientific groups. This effort is greatly appreciated.