The Boundary Layer Equations and a Dimensional Split Method for Navier-Stokes Equations in Exterior Domain of a Spheroid and Ellipsoid ()
1. Introduction
In computational fluid dynamics, one need to compute the drag exerted on a body in flow field; in particular, optimal shape design has received considerable attention already, see Li and Huang [1] , Li, Chen and Yu [2] , and Li, Su, Huang [3] . It has become vast enough to branch into several disciplines on the theoretical side, many results deal with the existence of solutions to the problem or its relaxed form, on the practical side, topological shape 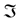 optimization which solves numerically the relaxed problem or by local shape variation. In this case
optimization which solves numerically the relaxed problem or by local shape variation. In this case
we have to compute the velocity gradient 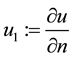 along the normal to the surface of the boundary and normal
along the normal to the surface of the boundary and normal
stress tensor 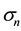 to the surface. All those computation have to do in the boundary layer. Therefore this leads to make very fine mash; for example, 80% nodes will be concentred in a neighborhood of the surface of the body.
to the surface. All those computation have to do in the boundary layer. Therefore this leads to make very fine mash; for example, 80% nodes will be concentred in a neighborhood of the surface of the body.
In this paper a boundary layer equations for  on the surface will be established using local
on the surface will be established using local
semi-geodesic coordinate system based on the surface, provide the computational formula for the drag func- tional. In addition, a dimensional split method for three dimensional Navier-Stokes equations is established by applying several 2D-3C partial differential equations on the two dimensional manifolds to approximate 3D Navier-Stokes equation.
The Dimensional Slitting Methods deal, for examples, with thin domain problem as elastic shell (see Ciarlet [4] , Li, Zhang and Huang [5] ), Temam and Ziane [6] , and with boundary value problem with complexity boun- dary geometry (see [7] -[10] ).
The content of the paper is organized as the followings. Section 2 establishes semi-geodesic coordinate system and related the Navier-Stokes equations; Section 3 assumes that the solutions of Navier-Stokes equa- tions in the boundary layer can be made Taylor expansion with respect to transverse variable, derive the equations for the terms of Taylor expansion; Section 4 proves the existence of the solutions of the BLE; Section 5 provides the computational formula of the drag functional; Section 6 provide a dimensional splitting method for 3D Navier-Stokes equations; Section 7 provide some examples.
2. Navier-Stokes Equations and Its Variational Formulation in a Semi-Geodesic Coordinate System
Through this paper, we consider state steady incompressible Navier-Stokes equations and its variational formu- lation in a thin domain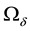 , a strip with thickness
, a strip with thickness 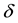 and by a Lipchsitz continuous boundary
and by a Lipchsitz continuous boundary
 ,
,
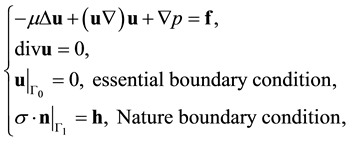 (2.1)
(2.1)
or
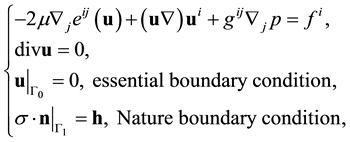 (2.1')
(2.1')
which are invariant form in any curvilinear coordinate system. Let
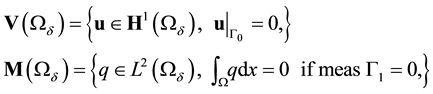
At first, we introduce semi-geodesic coordinate system (abbreviation S-coordinate). As well known thhat boundary layer 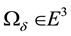 in 3D Euclidean space bounded by
in 3D Euclidean space bounded by 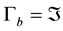 and
and 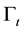 where
where 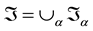 is bottom of the boundary layer, a surface of solid boundary of the flow fluid, and
is bottom of the boundary layer, a surface of solid boundary of the flow fluid, and 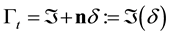 is a top boundary of
is a top boundary of , an artificial interface of the flow fluid where
, an artificial interface of the flow fluid where ![]() is unit normal vector to
is unit normal vector to ![]() and
and ![]() is a parameter, the
is a parameter, the
thickness of the strip, the boundary layer. Assume that there exits a smooth immersion ![]() such that
such that ![]() are linearly independent where
are linearly independent where ![]() is a Lipschitz domain with boundary
is a Lipschitz domain with boundary ![]() and
and ![]() are parameters which are called Gaussian coordinate on the surface
are parameters which are called Gaussian coordinate on the surface![]() . It is
. It is
obvious that ![]() are basis. So the geometry of the surface
are basis. So the geometry of the surface ![]() is given by first fundamental form and second
is given by first fundamental form and second
fundamental form and third fundamental form which coefficients are metric tensor ![]() and curvature tensor
and curvature tensor ![]() and tensor
and tensor ![]() respectively where
respectively where ![]() is unit normal vector to
is unit normal vector to ![]()
![]()
Their contravariant components ![]() are given by
are given by
![]()
What’s follows that we will frequently used the inverse matrix ![]() of
of![]() :
:
![]()
Now, assume that there exists an unique normal vector ![]() to
to ![]() from each point
from each point ![]() such that (see Figure 1)
such that (see Figure 1)
![]()
where ![]() is origin. Thereby, point
is origin. Thereby, point ![]() is determined by triple numbers
is determined by triple numbers![]() . Inversely, a triple numbers
. Inversely, a triple numbers ![]() can determine uniquely a point
can determine uniquely a point![]() . Curvilinear coordinate
. Curvilinear coordinate ![]() in
in ![]()
is called semi-geodesic coordinate based on the surface![]() . Its bases vectors are
. Its bases vectors are ![]() and the metric tensor
and the metric tensor ![]() of 3D Euclidean space
of 3D Euclidean space ![]() in this semi-geodesic coordinate are given by
in this semi-geodesic coordinate are given by
![]()
Therefore, the metric tensor of ![]() can be expressed by the metric tensor of
can be expressed by the metric tensor of ![]() in the semi-geodesic coor- dinate system:
in the semi-geodesic coor- dinate system:
![]()
Figure 1. The diagram of semi-geodesic coor- dinate system.
![]() (2.2)
(2.2)
(see ref. [1] ) wherre ![]() are mean curvature and Gaussian curvature of
are mean curvature and Gaussian curvature of![]() . Throughout this paper, we employ semi-geodesic coordinate system
. Throughout this paper, we employ semi-geodesic coordinate system ![]() based on the surface
based on the surface ![]() (see [1] and Figure 1) (later
(see [1] and Figure 1) (later
on, denote ![]() -coordinate). The metric tensor of
-coordinate). The metric tensor of ![]() in this coordinate are denoted by
in this coordinate are denoted by![]() . It is obvious that the determinate
. It is obvious that the determinate ![]() if
if ![]() is small enough. Hence coordinate
is small enough. Hence coordinate ![]() is nonsingular.
is nonsingular.
In addition, we review the main notation. Greek indices and exponents belong to the set![]() , while Latin indices and exponents (except when otherwise indicated, as when they are used to index sequences) belong to the set
, while Latin indices and exponents (except when otherwise indicated, as when they are used to index sequences) belong to the set![]() , and the summation convention with respect to repeated indices and exponents is systematically
, and the summation convention with respect to repeated indices and exponents is systematically
used. Symbols such as ![]() or
or ![]() designate the Kronecker’s symbol. The Euclidean scalar product and the the exterior product of
designate the Kronecker’s symbol. The Euclidean scalar product and the the exterior product of ![]() are noted
are noted ![]() and
and![]() ; the Euclidean norm of
; the Euclidean norm of ![]() is noted
is noted![]() . Fur-
. Fur-
thermore, the physical or geometric quantities with the asterisk ![]() express the quantities on the manifold
express the quantities on the manifold![]() , for example,
, for example, ![]() is covariant derivative on
is covariant derivative on![]() . Furthermore, the physical or geometric quantities with the asterisk
. Furthermore, the physical or geometric quantities with the asterisk ![]() express the quantities on the manifold
express the quantities on the manifold![]() , for example,
, for example, ![]() is covariant derivative on
is covariant derivative on![]() . Further- more, the notations
. Further- more, the notations ![]() are given contravariant components and covariant components of the permuta- tion tensor on
are given contravariant components and covariant components of the permuta- tion tensor on ![]()
![]()
There are following relations of the first,second and third fundamental forms (ref. [1] )
![]()
The following give the relations of differential operators in the space and on ![]() (see [1] ). For example, under the
(see [1] ). For example, under the ![]() -coordinate system, the Christoffel symbols of
-coordinate system, the Christoffel symbols of ![]() and
and ![]() satisfy
satisfy
![]()
and covariant derivatives of the vector field are given by
![]()
where ![]() is covariant component of vector
is covariant component of vector![]() . The strain tensor of vector field in
. The strain tensor of vector field in ![]() and on
and on ![]() are given by respectively
are given by respectively
![]()
Of course,![]() ;
; ![]() Under the
Under the ![]() -coordinate system there are following formula for the covariant derivatives of the vectors in the space
-coordinate system there are following formula for the covariant derivatives of the vectors in the space ![]() and on the
and on the ![]() (ref. [1] )
(ref. [1] )
![]() (2.3)
(2.3)
The strain tensors of the vectors in ![]() and on
and on ![]() can be expressed as
can be expressed as
![]() (2.4)
(2.4)
where
![]() (2.5)
(2.5)
In the semi-geodesic coordinate system (see next section), define the bilinear form ![]() and trilinear form
and trilinear form ![]()
![]() (2.6)
(2.6)
Then, the primitive variable variational formulation for Navier-Stokes Equations (2.1') is given by
![]() (2.7)
(2.7)
while the Navier-Stokes Equations (2.7) in semi-geodesic coordinate system are expressed as
![]() (2.8)
(2.8)
![]() (2.9)
(2.9)
3. Boundary Layer Equations
Assume that ![]() is a two dimensional manifold parameterized by
is a two dimensional manifold parameterized by![]() . In the neighborhood of the orientate surface
. In the neighborhood of the orientate surface ![]() let define a surface
let define a surface![]() :
:
![]()
It is obvious that ![]() ia a geodesic parallel surface of
ia a geodesic parallel surface of ![]() and the geodesic distance each other is equal to
and the geodesic distance each other is equal to ![]() where
where ![]() is a small constant.In this paper we only consider exterior flow around a body occupied by
is a small constant.In this paper we only consider exterior flow around a body occupied by ![]() with a two dimensional manifold
with a two dimensional manifold ![]() without boundary. The boundary layer domain
without boundary. The boundary layer domain
![]()
Domain ![]() is called the “stream layer”.
is called the “stream layer”.
Assumption AI assume that the solutions ![]() of Navier-Stokes Equation (2.7) in boundary layer
of Navier-Stokes Equation (2.7) in boundary layer ![]() in semi-geodesic coordinate system and right term
in semi-geodesic coordinate system and right term ![]() can be made Taylor expansion with respect to the transverse variable
can be made Taylor expansion with respect to the transverse variable ![]()
![]() (3.1)
(3.1)
In same time, the test vector also can be made Taylor expansion
![]()
Theorem 1 In a boundary layer domain ![]() with non-slip boundary condition
with non-slip boundary condition![]() , if the Assumption AI (3.1) is satisfied, then nine unknown of
, if the Assumption AI (3.1) is satisfied, then nine unknown of ![]() satisfy following a system of three partial dif- ferential equations which are called boundary layer equations I (BLE I):
satisfy following a system of three partial dif- ferential equations which are called boundary layer equations I (BLE I):
![]() (3.2)
(3.2)
and five algebraic equations
![]() (3.3)
(3.3)
Associated variational formulations with (3.2) is given by
![]() (3.4)
(3.4)
where the bilinear forms defined by
![]() (3.5)
(3.5)
![]()
and
![]() (3.6)
(3.6)
where
![]()
![]() is normal stress tensor at
is normal stress tensor at ![]() (top boundary of boundary layer),
(top boundary of boundary layer), ![]() are defined by (3.1).
are defined by (3.1).
Next, let consider interface equation. In this case ![]() is a flexible surface (slip and passing through conditions).
is a flexible surface (slip and passing through conditions).
Assumption AII Assume that the solutions ![]() of Navier-Stokes Equation (2.1) in stream layer
of Navier-Stokes Equation (2.1) in stream layer
![]() in semi-geodesic coordinate system based on
in semi-geodesic coordinate system based on ![]() and right term
and right term ![]() can be made Taylor expansion with respect to the transverse variable
can be made Taylor expansion with respect to the transverse variable ![]()
![]() (3.7)
(3.7)
Theorem 2 Assume that the Assumption II is satisfied. Then six unknown of ![]() in (3.7) satisfy following system of the nonlinear partial differential equations which are called stream layer equations II (abbreviation SLE II) (interface equations):
in (3.7) satisfy following system of the nonlinear partial differential equations which are called stream layer equations II (abbreviation SLE II) (interface equations):
![]() (3.8)
(3.8)
![]() (3.9)
(3.9)
The right terms
![]() (3.10)
(3.10)
In particular, for flexible (slip condition![]() ) boundary surface
) boundary surface![]() , neglect hight order terms and keep one order term of
, neglect hight order terms and keep one order term of![]() , then (3.3) (3.4) and (3.5) become
, then (3.3) (3.4) and (3.5) become
The Proof of Theorems 1 and 2 is neglected.
4. The Existence of the Solution
In this section we prove the existence of the weak solution of (3.2). To do that we consider variational
formulation of (3.2). Let ![]() where
where ![]() is a sobolev space of 1-order with perio-
is a sobolev space of 1-order with perio-
dic boundary condition. Since ([14] , Th.1.8.6) we claim
![]()
where
![]()
Let define bilinear form:![]() ,
,
![]() (4.1)
(4.1)
where ![]() are two positive constants and
are two positive constants and ![]() and
and
![]()
Then corresponding variational formulation for (3.2) is given by
![]() (4.2)
(4.2)
where
![]() (4.3)
(4.3)
Lemma 1 Assume that the metric tensor and curvature tensor of ![]() satisfy
satisfy ![]() and
and ![]() respectively. Then viscosity tensor of
respectively. Then viscosity tensor of ![]()
![]() and metric tensor
and metric tensor ![]() are positive definition, i.e. for any symmetric matrix
are positive definition, i.e. for any symmetric matrix![]() , there exists two constants
, there exists two constants![]() ,
, ![]() independent of
independent of ![]() such that
such that
![]() (4.4)
(4.4)
Therefore,
![]() (4.5)
(4.5)
Furthermore, If ![]() and the thickness
and the thickness ![]() of boundary domain small enough, then bilinear form
of boundary domain small enough, then bilinear form ![]() is positive
is positive
![]() (4.6)
(4.6)
Proof The proof of (4.4) can be found in ([1] [4] ). It remain to prove (4.6). By virtue of the positive definition of metric tensor ![]() and assumption of lemma and using Hoelder inequality, we assert that
and assumption of lemma and using Hoelder inequality, we assert that
![]()
where ![]() is a constant independent of
is a constant independent of ![]() depending
depending![]() . The proof is complete.
. The proof is complete. ![]()
Lemma 2 Assume that the two-dimensional manifold ![]() is smooth enough such that the metric tensor
is smooth enough such that the metric tensor ![]() of
of ![]() and curvature tensor
and curvature tensor ![]() satisfy
satisfy![]() . Then the bilinear forms
. Then the bilinear forms ![]() defined by (4.1):
defined by (4.1): ![]() is symmetric, continuous
is symmetric, continuous
![]() (4.7)
(4.7)
where ![]() Furthermore if
Furthermore if ![]() is smaller enough such that
is smaller enough such that
![]() (4.8)
(4.8)
then they are also coercive respectively
![]() (4.9)
(4.9)
where ![]() is a constant independent of
is a constant independent of ![]() having different meaning at different place and
having different meaning at different place and
![]()
Proof Indeed it is enough to prove the coerciveness (4.8) since the continuous and symmetric are obvious by Hoelder inequality. Since Lemma 1,
![]()
In view of Korn inequality on Riemann manifold (see [4] Th.1.7.9 )
![]()
we assert that
![]() (4.10)
(4.10)
if ![]() satisfies
satisfies ![]() To sum up, we conclude our proof.
To sum up, we conclude our proof. ![]()
Next we consider variational problem (4.2) corresponding to boundary layer Equation (3.4). Let
![]() (4.11)
(4.11)
Lemma 3 Assume that the manifold ![]() satisfies that
satisfies that ![]() such that there exists a constant
such that there exists a constant ![]()
![]()
The thickness ![]() of the boundary layer is small enough. Then bilinear form
of the boundary layer is small enough. Then bilinear form ![]() defined by (4.11) is continuous:
defined by (4.11) is continuous:
![]() (4.12)
(4.12)
where ![]() and also satisfies following inequality
and also satisfies following inequality
![]() (4.13)
(4.13)
where ![]() is small enough and parameters
is small enough and parameters ![]() satisfy
satisfy
![]() (4.14)
(4.14)
Proof It is easy to verify (4.12) by applying Hoelder inequality and Poincare inequality. It remains to prove (4.13). At the first, we recall that the assumptions of the lemma shows
![]()
Taking (4.8) into account, from (4.10) it infers
![]() (4.15)
(4.15)
(1) Since Lemma 1 and (4.3) we have
![]()
Moreover, using Godazzi formula![]() , we obtain
, we obtain
![]()
Therefore
![]()
Thanks to
![]()
![]() (4.16)
(4.16)
We assert that
![]()
Second inequality shows
![]() (4.17)
(4.17)
Using Young inequality
![]()
we have
![]() (4.18)
(4.18)
By similar manner,
![]() (4.19)
(4.19)
![]() (4.20)
(4.20)
Substituting (4.18-4.20) into (4.16) leads to
![]() (4.21)
(4.21)
Taking (4.9) into account, it yield
![]() (4.22)
(4.22)
If
![]() (4.23)
(4.23)
Then
![]() (4.24)
(4.24)
It is easy to verify that (4.23) is satisfied if the parameters ![]() in the definition (4.1) are held
in the definition (4.1) are held
![]() (4.25)
(4.25)
Next we consider trilinear form. Taking into account of
![]()
we claim that
![]()
By Ladyzhenskya inequality (Temam [11] )
![]() (4.26)
(4.26)
it infers that
![]() (4.27)
(4.27)
Combing (4.15) (4.24) and (4.27), we obtain
![]() (4.28)
(4.28)
This complete our proof. ![]()
Theorem 3 Assume that the hypotheses in Lemma 3 are satisfied and the mapping
![]()
is sequentially weakly continuous in ![]()
![]()
Then there exists at least one solution ![]() of (4.2) satisfying
of (4.2) satisfying
![]() (4.29)
(4.29)
where ![]() is the thickness of boundary layer,
is the thickness of boundary layer, ![]() are constants defined in the followings.
are constants defined in the followings.
Proof We begin with constructing a sequence of approximate solutions by Galerkin’s method. Since the space ![]() is a separable Hilbert space, there exist sequence
is a separable Hilbert space, there exist sequence ![]() in
in ![]() such that: 1) for all
such that: 1) for all![]() , the elements
, the elements ![]() are linearly independent; 2) the finite linear combinations of the
are linearly independent; 2) the finite linear combinations of the ![]() are dense in
are dense in![]() . Such sequence
. Such sequence ![]() are called a basis of the separable space. Denote by
are called a basis of the separable space. Denote by ![]() the subspace of
the subspace of ![]() spanned by finite sequence
spanned by finite sequence![]() . Then we solve an approximate problem of (4.2)
. Then we solve an approximate problem of (4.2)
![]() (4.30)
(4.30)
Setting
![]()
Problem (4.30) is equivalent to a system of nonlinear equations with m unknowns![]() . For each
. For each ![]() problem (4.30) has at least one solution. In fact, when defining a mapping
problem (4.30) has at least one solution. In fact, when defining a mapping ![]() by
by
![]()
where ![]() is the scalar product in
is the scalar product in![]() ,
, ![]() is a solution of problem (4.30) if only if
is a solution of problem (4.30) if only if ![]() Since
Since
![]()
it follows from (4.28)
![]()
Let ![]() Furthermore, assume that
Furthermore, assume that
![]() (4.31)
(4.31)
if ![]() is small enough. Then
is small enough. Then
![]() (4.32)
(4.32)
if
![]() (4.33)
(4.33)
Hence, we conclude
![]() (4.34)
(4.34)
Moreover, ![]() is continuous in a finite dimension space
is continuous in a finite dimension space![]() , we can apply following lemma ([12] ).
, we can apply following lemma ([12] ).
Lemma 4 Let ![]() be a finite dimensional Hilbert space whose scalar product is denoted by
be a finite dimensional Hilbert space whose scalar product is denoted by ![]() and the corresponding norm by
and the corresponding norm by![]() . Let
. Let ![]() be a continuous mapping from
be a continuous mapping from ![]() into
into ![]() with the following property: there exists
with the following property: there exists ![]() such that
such that
![]() (4.35)
(4.35)
Then, there exists an element ![]() in
in ![]() such that
such that
![]() (4.36)
(4.36)
Therefore there exists a solution ![]() for problem (4.30) with
for problem (4.30) with
![]() (4.37)
(4.37)
This shows that the sequence (![]() of the solutions to (4.30) in
of the solutions to (4.30) in ![]() are uniformly bounded. Therefore we can extract a subsequence (still denoted by
are uniformly bounded. Therefore we can extract a subsequence (still denoted by![]() ) such that
) such that
![]()
Then, the compactness of the embedding of ![]() into
into ![]() implies that
implies that
![]()
Since ![]() is dense in
is dense in![]() , it is obvious that if
, it is obvious that if
![]()
Taking the limit of both sides of (4.30) implies
![]()
therefore
![]()
Then ![]() is a solution of (4.2) and which satisfies
is a solution of (4.2) and which satisfies
![]()
The proof is complete. ![]()
Remark The mapping ![]() is sequentially weakly continuous in
is sequentially weakly continuous in ![]() can be found in [3] .
can be found in [3] .
5. Dimensional Split Method for Exterior Flow Problem around an Obstacle and a Two Scale Parallel Algorithms
In this section, we proposal a dimensional split algorithm for the three dimensional exterior flow around a obstacle occupied by![]() .
. ![]() is a smooth surface of the obstacle and
is a smooth surface of the obstacle and![]() . Assume that
. Assume that ![]() is decomposed by a series of geometric parallel surfaces
is decomposed by a series of geometric parallel surfaces ![]() into a series of stream layer
into a series of stream layer ![]() bounded by
bounded by ![]() such that
such that![]() .
.
On every surface![]() , it generalis a global system including one system of BLE I on the boundary surface
, it generalis a global system including one system of BLE I on the boundary surface ![]() of the obstacle and N-1 systems of flexible boundary equations BLE II on
of the obstacle and N-1 systems of flexible boundary equations BLE II on![]() :
:
![]()
where right terms are given by
![]()
The features of these systems are that the right terms of them depend upon the solution of next system, for example, the right term of kth-system depend upon the solution of ![]() th. system. It is better to apply alterative iteration algorithm to solve these systems. That is
th. system. It is better to apply alterative iteration algorithm to solve these systems. That is
(1) Suppose that right hands![]() , are known;
, are known;
(2) Solve system of ![]()
(3) Modifying ![]() by using results obtained , then goto (2) to be continuous until reach certainly accuracy.
by using results obtained , then goto (2) to be continuous until reach certainly accuracy.
In order to find solution of Navier-Stokes equations at any point P in Exterior domain ![]()
(i) Identify point P in which stream layer ![]() bounded by
bounded by![]() , then set
, then set ![]() in local coordinate system;
in local coordinate system;
(ii) ![]()
where ![]() are solution of BLE on
are solution of BLE on![]() .
.
In details,
(I) For ![]() i.e. solid surface with non-slip boundary condition, we give the boundary layer equations BLE I (3.2) on the boundary surface
i.e. solid surface with non-slip boundary condition, we give the boundary layer equations BLE I (3.2) on the boundary surface ![]() of obstacle. from Theorem 2, three unknown
of obstacle. from Theorem 2, three unknown ![]() solve
solve
![]() (5.1)
(5.1)
and six unknown ![]() can be found by six algebraic equations
can be found by six algebraic equations
![]() (5.2)
(5.2)
Associated variational formulations with (5.1) is given by
![]() (5.3)
(5.3)
where ![]() are two positive arbitrary constants, the bilinear forms and trilinear form are
are two positive arbitrary constants, the bilinear forms and trilinear form are
![]() (5.4)
(5.4)
and
![]() (5.5)
(5.5)
The right terms are given by
![]() (5.6)
(5.6)
where![]() .
.
(II) For![]() , i.e. on flexible surfaces, corresponding boundary layer equations SLE II (for
, i.e. on flexible surfaces, corresponding boundary layer equations SLE II (for![]() ) at flexible surface (artificial interface)
) at flexible surface (artificial interface)![]() ,
, ![]() are given by (3.8) and (3.9)
are given by (3.8) and (3.9)
![]() (5.7)
(5.7)
![]() (5.8)
(5.8)
![]() (5.9)
(5.9)
On the other hand we can improve (5.7). To do that, making covariant derivative ![]() on both sides of the first equation in (3.9) and combining last equation in (3.9),
on both sides of the first equation in (3.9) and combining last equation in (3.9), ![]() can be found by
can be found by
![]() (5.10)
(5.10)
![]() (5.11)
(5.11)
The variational formulations corresponding to (5.7) and (5.1) are given respectively by
![]() (5.12)
(5.12)
and
![]() (5.12')
(5.12')
where the bilinear forms and linear form are defined by
![]() (5.13)
(5.13)
(III) For ![]() i.e. a last artificial interface Surface
i.e. a last artificial interface Surface![]() . There are two choices to do that (1) assume that
. There are two choices to do that (1) assume that ![]() on
on ![]() where
where ![]() is known infinity up stream flow velocity. (2) we assume that the flow outside
is known infinity up stream flow velocity. (2) we assume that the flow outside ![]() is governed by Oseen equation and give a boundary integrating equation on
is governed by Oseen equation and give a boundary integrating equation on ![]() via fundamental solution of Oseen equations.
via fundamental solution of Oseen equations.
(1) Let ![]() is Cartesian coordinate and
is Cartesian coordinate and ![]() where
where ![]() are base vectors. The surface
are base vectors. The surface ![]() can be parametrization by
can be parametrization by ![]() where
where ![]() are parameters, i.e. are Gaussian
are parameters, i.e. are Gaussian
coordinate on![]() . Then base vectors
. Then base vectors ![]() and unit normal vector
and unit normal vector ![]() in semi-coordinate on
in semi-coordinate on ![]() are given by
are given by
![]() (5.14)
(5.14)
while the metric tensor ![]() and curvature tensor
and curvature tensor ![]() are given
are given
![]() (5.15)
(5.15)
where![]() . Our aim is to give boundary conditions on
. Our aim is to give boundary conditions on![]() . Owing to (4.12) we claim
. Owing to (4.12) we claim
![]()
On other hand, we show
![]()
Indeed,
![]()
Finally we imply
![]() (5.16)
(5.16)
where ![]() is describing
is describing![]() . (5.16) will be used for solving BLE I on
. (5.16) will be used for solving BLE I on ![]() with
with![]() .
.
(2). Let assume that the flow outside of ![]() is governed by Oseen equation
is governed by Oseen equation
![]() (5.17)
(5.17)
![]() is known and
is known and ![]() is a well known vector, for example
is a well known vector, for example![]() , and
, and![]() , and
, and ![]() are solutions of 2D-3C Navier-Stokes equations on the
are solutions of 2D-3C Navier-Stokes equations on the![]() . Furthermore,
. Furthermore, ![]() is normal stress tensor to be found in the section. Let
is normal stress tensor to be found in the section. Let ![]() be a Cartesian coordinate.
be a Cartesian coordinate. ![]() are fundamental solutions of the follow- ing equations
are fundamental solutions of the follow- ing equations
![]() (5.18)
(5.18)
![]() can be expressed as
can be expressed as
![]() (5.19)
(5.19)
where ![]() is a fundamental solution of following equation
is a fundamental solution of following equation
![]() (5.20)
(5.20)
where for ![]()
![]() (5.21)
(5.21)
where ![]() is a Bessel function of second kind.
is a Bessel function of second kind.
Then integral expressions of solutions of Oseen problem (5.9) are given by
![]() (5.22)
(5.22)
where ![]() is stress tensor
is stress tensor
![]()
![]()
Here we employ Cartesian coordinate system ![]() and artificial surface
and artificial surface ![]() is a two
is a two
dimensional manifold. The integrate representation (5.17) of the solution of Oseen problem is invariant, it is valid for any curvature coordinate. Since formula for fundamental solution ![]() is represent at Cartesian coordinate. It also can be compute at any curvature coordinate according transformation rule of tensor of one order.
is represent at Cartesian coordinate. It also can be compute at any curvature coordinate according transformation rule of tensor of one order.
Vector ![]() in (5.17) is normal stress tensor at
in (5.17) is normal stress tensor at ![]()
![]() The normal stress tensor
The normal stress tensor ![]() at
at ![]() is continuous
is continuous![]() . This means that
. This means that ![]() on both sides of
on both sides of ![]() are coincidental.
are coincidental.
Normal stress tensor ![]() on the artificial boundary
on the artificial boundary ![]() satisfies following equation
satisfies following equation
![]() (5.23)
(5.23)
(5.23) can be rewrite in semi-geodesic coordinate based on![]() :
:
![]() (5.24)
(5.24)
where, ![]() is semi-geodesic coordinate. By the transformation of coordinate,
is semi-geodesic coordinate. By the transformation of coordinate, ![]() where
where ![]() are Cartesian coordinate and
are Cartesian coordinate and ![]() is the parametrization representation of the surface
is the parametrization representation of the surface![]() .
.
Lemma 5 The bilinear form ![]() defined by (5.23) is symmetric, continuous and coercive from
defined by (5.23) is symmetric, continuous and coercive from ![]() into
into ![]()
![]()
Theorem 4 Assume that ![]() are smooth and bounded in
are smooth and bounded in ![]() Then there exists a unique solution of following variational problem
Then there exists a unique solution of following variational problem
![]() (5.25)
(5.25)
Parallel algorithms. The Domain ia made partition by m interfaces surfaces and we obtain ![]() the systems of BLE I and SLE II. Solving each BLE I and SLE II independently, then applying alternatively iterative algorithm are performance at the same time. On the other hand, the parallel algorithms for BLE I and SLE II can be used. Therefore, parallel algorithms are applied in two direction at the same time.
the systems of BLE I and SLE II. Solving each BLE I and SLE II independently, then applying alternatively iterative algorithm are performance at the same time. On the other hand, the parallel algorithms for BLE I and SLE II can be used. Therefore, parallel algorithms are applied in two direction at the same time.
6. Computation of the Drag
The drag is a force exerted on a solid boundary surface, for example,![]() . There is normal stress on
. There is normal stress on ![]() which can expressed under semi-geodesic coordinate based on
which can expressed under semi-geodesic coordinate based on ![]() by
by
![]()
The drag is a projection of normal stress on the direction of infinite stream flow![]() . Hence
. Hence
![]() (6.1)
(6.1)
Since unit normal vector at ![]() is
is ![]() and by (5.1)
and by (5.1)
![]() (6.2)
(6.2)
Therefore
![]()
As well known that the stress tensor is given by
![]()
At surface ![]()
![]()
![]()
Since
![]()
because of
![]()
Hence
![]() (6.3)
(6.3)
The drag is a force exerted on a solid boundary surface, for example,![]() . There is normal stress on
. There is normal stress on ![]() which can be expressed under semi-geodesic coordinate based on
which can be expressed under semi-geodesic coordinate based on ![]() by
by![]() . The drag is a pro- jection of normal stress on the direction of infinite stream flow
. The drag is a pro- jection of normal stress on the direction of infinite stream flow![]() . Hence
. Hence
![]() (6.4)
(6.4)
where ![]() are parameter representation of
are parameter representation of![]() .
.
7. Examples
7.1. The Flow around a Sphere
Assume that ![]() and
and ![]() are Cartesian and spherical coordinates respectively
are Cartesian and spherical coordinates respectively
![]()
Simple calculations show that the metric tensor of spherical surface![]() . is given
. is given
![]() (7.1)
(7.1)
The tensor of second fundamental form, i.e. curvature tensor of spherical surface is given by
![]() (7.2)
(7.2)
the base vectors of semi-geophysical coordinate system are given
![]() (7.3)
(7.3)
We remainder have to give the covariant derivatives of the velocity field, Laplace-Betrami operator and trace-Laplace operator. To do this we have to give the first and second kind of Christoffel symbols on the spherical surface ![]() as a two dimensional manifolds
as a two dimensional manifolds
![]()
Then covariant derivatives of vector ![]() on the two dimensional manifold
on the two dimensional manifold ![]() is given by
is given by
![]()
Nonlinear terms
![]()
and
![]()
The associated Laplace-Betrami operator and divergence operator on ![]() are given by
are given by
![]() (7.4)
(7.4)
while trace-Laplace operator on ![]()
![]() (7.5)
(7.5)
(A) BLE I
Substituting previous formula into Theorem 1 we assert that
![]() (7.6)
(7.6)
In particular, if the flow is axial symmetric then
![]() (7.7)
(7.7)
where
![]()
(5.7) is a two points boundary value problem for ordinary differential equations.
![]() (7.8)
(7.8)
![]() (7.9)
(7.9)
(B) SLE II
The first, we note
![]()
So that
![]()
Taking (5.7) into account, we claim that
![]()
(7.10)
If the flow is symmetric then
![]() (7.11)
(7.11)
and
![]()
(7.12)
where
![]() (7.13)
(7.13)
The drag is given by
![]() (7.14)
(7.14)
7.2. The Flow around an Ellipsoid
Let parametric equation of the ellipsoid be given by
![]() (7.15)
(7.15)
where ![]() are Cartesian basis,
are Cartesian basis, ![]() are the parameters and
are the parameters and ![]() are called Guassian co- ordinates of ellipsoid. The base vectors on the ellipsoid
are called Guassian co- ordinates of ellipsoid. The base vectors on the ellipsoid
![]()
The metric tensor of the ellipsoid is given by
![]() (7.16)
(7.16)
Curvature tensor, mean curvature and Gaussian curvature are given by
![]() (7.17)
(7.17)
Semi-Geodesic Coordinate System Based on Ellipsoid ![]()
That is
![]()
The radial vector at any point in ![]()
![]()
![]()
Corresponding metric tensor of ![]() are given by (2.1). We remainder to give the covariant derivatives of the velocity field, Laplace-Betrami operator and trace-Laplace operator. To do this we have to give the first and second kind of Christoffel symbols on the ellipsoid
are given by (2.1). We remainder to give the covariant derivatives of the velocity field, Laplace-Betrami operator and trace-Laplace operator. To do this we have to give the first and second kind of Christoffel symbols on the ellipsoid ![]() as a two dimensional manifolds
as a two dimensional manifolds
![]()
Then covariant derivatives of vector ![]() on the two dimensional manifold
on the two dimensional manifold ![]()
![]() (7.18)
(7.18)
The associated Laplace-Betrami operator on ![]()
![]() (7.19)
(7.19)
Trace-Laplace operatoe on ![]()
![]()
![]() (7.20)
(7.20)
In addition, nonlinear terms
![]() (7.21)
(7.21)
and linear terms
![]() (7.22)
(7.22)
(i) BLE I. Taking (5.1-5.6) and above formula into account we obtain BLE I on the ellipsoid
![]() (7.23)
(7.23)
where
![]() (7.24)
(7.24)
![]() (7.25)
(7.25)
The right terms are given by
![]() (7.26)
(7.26)
(ii) SEL II. Let consider SEL II given by (5.7) and corresponding variational formulation (5.12) which are followings in semi geodesic coordinate system based on the ellipsoid
![]()
(7.27)
where
![]() (7.28)
(7.28)
![]() (7.29)
(7.29)
![]() (7.30)
(7.30)
Calculation of Drag Assume that
![]()
![]() (7.31)
(7.31)
(iii) Axial symmetry Case. If![]() , then boundary layer Equation (7.23) is axial symmetry with
, then boundary layer Equation (7.23) is axial symmetry with ![]() -axes. Indeed, in this case,
-axes. Indeed, in this case,
![]() (7.32)
(7.32)
The covariant derivatives become
![]() (7.33)
(7.33)
![]() (7.34)
(7.34)
![]() (7.35)
(7.35)
Let
![]()
Then BLE I (7.23) and SLE II (7.27) become
![]() (7.36)
(7.36)
where
![]() (7.37)
(7.37)
The drag is given by
![]() (7.38)
(7.38)
In the following we concern with the axi-symmetric flow around an ellipsoid, which depends significantly on the Reynolds number and the geometry of the ellipsoid. And the boundary layer equations are solved with spectral method. The fluid approaches the ellipsoid with a uniform free-stream velocity from inlet to outlet. In order to compare with the results in reference conveniently, the results should be dimensionless. Therefore the other parametric equation of ellipsoid is proposed
![]()
where ![]() a constant and the parameter
a constant and the parameter ![]() defines the surface of the spheroid and is related to the axis ratio by
defines the surface of the spheroid and is related to the axis ratio by![]() . A perfect sphere would be represented by
. A perfect sphere would be represented by ![]() whereas a flat circular disk would be represented by
whereas a flat circular disk would be represented by![]() .
.
The Reynolds number based on the focal length, i.e.![]() , varies from 0.1 to 1.0. In the case the
, varies from 0.1 to 1.0. In the case the
focal length ![]() is the reference length and inlet velocity
is the reference length and inlet velocity ![]() is the reference velocity. Let the total drag coefficient be,
is the reference velocity. Let the total drag coefficient be,
![]()
where ![]() is the spheroid projected area. From BLE I the total drag includes two terms and the first term is the pressure part while the second term is the viscous part, i.e.
is the spheroid projected area. From BLE I the total drag includes two terms and the first term is the pressure part while the second term is the viscous part, i.e.![]() , which are defined as,
, which are defined as,
![]()
Therefore the total drag coefficient is also decomposed into pressure and viscous part:![]() , in which,
, in which,
![]()
Firstly the numerical solution of boundary layer equations is validated quantitatively by comparison with results in references and finite element method. Table 1 presents results of pressure and total drag coefficients for various Reynolds numbers at![]() . Table 2 presents results of pressure and total drag coefficients for various values of
. Table 2 presents results of pressure and total drag coefficients for various values of ![]() at
at![]() . An excellent agreement between the present results and that of Alassar and
. An excellent agreement between the present results and that of Alassar and
Badr [13] are both achieved. And the normal stress tensor ![]() to the supper surface of boundary layer is
to the supper surface of boundary layer is
considered as the boundary condition of boundary layer equations, which is obtained from the solutions of finite element method. According to Table 1 and Table 2 the precision of drag computation with boundary layer equations is higher than the finite element method, so the boundary layer equations could be used to improve the computation precision of flow in the boundary layer with low cost.
Figure 2 presents the nearly stationary streamline patterns and pressure distributions at different Reynolds numbers 10, 30, 60 and 100 respectively for![]() . Here we note that our streamline patterns are similar to those obtained by Rimon and Cheng [14] for the sphere, since the separation angles and wake lengths are in close agreement with each other. Figure 2(b) shows a clearly visible secondary vortex at
. Here we note that our streamline patterns are similar to those obtained by Rimon and Cheng [14] for the sphere, since the separation angles and wake lengths are in close agreement with each other. Figure 2(b) shows a clearly visible secondary vortex at![]() , in this regard our result is also consistent with Rimon and Cheng’s [14] in spite of the difference in the size of the wake. Furthermore, Figure 2(d) shows a nice structure which corresponds to the a phenomenon observed for the flow around a circular cylinder. Since secondary vortices appear only at relatively high Reynolds number, we may conclude that the wake region is much more active at higher Reynolds number rather than that the wake length has to increase with the Reynolds number.
, in this regard our result is also consistent with Rimon and Cheng’s [14] in spite of the difference in the size of the wake. Furthermore, Figure 2(d) shows a nice structure which corresponds to the a phenomenon observed for the flow around a circular cylinder. Since secondary vortices appear only at relatively high Reynolds number, we may conclude that the wake region is much more active at higher Reynolds number rather than that the wake length has to increase with the Reynolds number.
Figure 3 presents the nearly stationary streamline patterns and pressure distributions at different ![]() 0.25, 0.5, 1.0 and 1.5 respectively for
0.25, 0.5, 1.0 and 1.5 respectively for![]() . As expected, no separation occurs at the low Re values.
. As expected, no separation occurs at the low Re values.
![]()
Table 1. Comparison of drag coefficients for various Reynolds numbers at![]() .
.
Then the flow details around the trailing edge of ellipsoid for![]() ,
, ![]() are given in Figure 4. It is obvious that the secondary vortex appears in the result of BLE, so more details could be computed by BLE than FEM. Although these flow details is obtained by FEM, its computational cost would be much more expensive than BLE. Let dimensionless pressure be
are given in Figure 4. It is obvious that the secondary vortex appears in the result of BLE, so more details could be computed by BLE than FEM. Although these flow details is obtained by FEM, its computational cost would be much more expensive than BLE. Let dimensionless pressure be ![]() and the definition of
and the definition of ![]() is as follows,
is as follows,
![]()
Figure 5 shows shows the surface dimensionless pressure distributions for the case ![]() when
when![]() , 30, 60 and 100. As Re increases, the difference in the pressure between the front and the rear stagnation points increases.
, 30, 60 and 100. As Re increases, the difference in the pressure between the front and the rear stagnation points increases.
Figure 6 proposes the corresponding pressure distributions in 3D.
![]() (a) (b)
(a) (b)
Figure 4. Comparison of flow details for![]() ,
,![]() : (a) FEM; (b) BLE.
: (a) FEM; (b) BLE.
![]()
Figure 5. Surface pressure distribution for![]() .
.
The effect of ![]() on the pressure distribution can be seen in Figure 7. The figure which show the results at
on the pressure distribution can be seen in Figure 7. The figure which show the results at ![]() when
when![]() , 0.5, 1.0 and 1.5 indicates that when
, 0.5, 1.0 and 1.5 indicates that when ![]() decreases, a positive pressure gradient may
decreases, a positive pressure gradient may
be expected. The surface pressure distributions are compared between FEM and BLE in Figure 8 for the case ![]() when
when![]() , 0.5, 1.0 and 1.5. The pressure distributions obtained by FEM and BLE are almost the same, however the absolute value of pressure in FEM is generally a little higher than these in BLE, which is consistent with the results in Table 2.
, 0.5, 1.0 and 1.5. The pressure distributions obtained by FEM and BLE are almost the same, however the absolute value of pressure in FEM is generally a little higher than these in BLE, which is consistent with the results in Table 2.
Figure 9 proposes the corresponding pressure distributions in 3D.
![]()
Figure 7. Surface pressure distribution for![]() .
.
![]()
Table 2. Comparison of drag coefficients for various values of ![]() at
at![]() .
.
Finally, it has to be emphasized that since flow axisymmetry is assumed in the present study, none of our results give any indication about symmetry-breaking in a real flow. The presented method are, however, not restricted to axi-symmetric flow, the BLE I aforementioned could be used to compute the non-axisymmetric flow.
Support
Supported by Major Research Plan of NSFC (91330116), National Basic Research Program No 2011CB 706505, NSFC 11371288, 11371289.