1. Introduction
The theoretic physicists consider that quantum gravity is holy land in the modern physics. In fact, the physicists always try to unify quantum gravity with General Relativity which is the most famous theorems in the twentieth century. In the hardship work, they virtually put forward the concepts from Superstring to loop quantum gravity. In the micro-scale, all quantum gravity theorems predict that approaching to the Planck scale, the classical picture of space-time break down, with space-time becoming somewhat “fuzzy” (or “foamy”) [1] -[5] . On the other hand, the problem of the flat rotation curves and the stability of cold stellar disks has been agonizing the astrophysicists for a long time. In 1982, Joe E. Tohline combines the observation data into the numerical calculation and put forward a new viewpoint. If the gravitational force would fall off as  instead of as
instead of as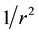 , the flat rotation curves will be solved without invoking the presence of Dark Matter [6] . But his model obviously violated the Newtonian gravity laws. In the last century, everything is confined with the observation technology. Until 2003, WMAP make fundamental measurements of cosmology―the study of the properties of our Universe as a whole.
, the flat rotation curves will be solved without invoking the presence of Dark Matter [6] . But his model obviously violated the Newtonian gravity laws. In the last century, everything is confined with the observation technology. Until 2003, WMAP make fundamental measurements of cosmology―the study of the properties of our Universe as a whole.
We realize the need of the Dark Energy and the Dark Matter in the Universe. So in the Solar system, the Dark Energy and the Dark Matter should be in existence in a mysterious mode. In fact, measurements of non-circular motions in the Milky Way have shown that there is actually very little room for an axisymmetric distribution of Dark Matter inside the Solar radius [7] [8] . But what are the nature of the Dark Energy and the Dark Matter? Nobody can answer until now.
Thus, supposing that ordinary atoms (also called baryons) are composed of Dark Matter and Dark Energy in the Universe the mass of Baryons originated from the coupling between Dark Matter and Dark Energy. Dark Matter and Dark Energy are the most elementary units in the Universe. So we can directly modify the Newtonian laws of gravity by introducing Planck scale for the model simplification. Then, the term of Newtonian gravity is separated into two parts. Considering the description of Dark Matter and Dark Energy, the positive part is corresponding with Dark Matter, and the negative part is corresponding with Dark Energy. The paper sets up a novel interaction model of Dark Matter and Dark Energy. Using the new model, the paper studies the characteristic property of the gravity in the very early Universe.
2. The Novel Model about Dark Matter and Dark Energy
Now, we introduce Planck scale into the Newton gravitational force term, and study the new characteristic property in the interaction presentation.
If 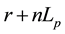 replaces
replaces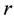 , namely:
, namely:
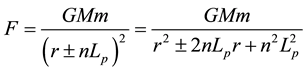 (1)
(1)
where 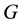 is the gravity constant,
is the gravity constant, 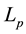 is Planck length
is Planck length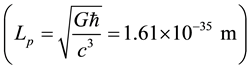 , n is an integral number
, n is an integral number
as the tuning parameter of scale,  is the distance between
is the distance between  with
with .
.
The new gravitational force equation keeps the characteristic property of long range force. And it is applicable in the Solar system. Additionally, it can match the new experimental data in the sub-micrometer range by tuning the parameter .
.
In the paper, the minimum distance is the atom scale  for the astrogeodesy. It is greatly larger than the Planck scale
for the astrogeodesy. It is greatly larger than the Planck scale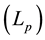 . Namely:
. Namely: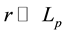 ,
,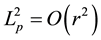 .
.
Therefore, the gravitational force equation changes into:
![]() (2)
(2)
If![]() , so Equation (2) is expressed as follows:
, so Equation (2) is expressed as follows:
![]() (3)
(3)
If![]() , so Equation (3) is expressed as follows:
, so Equation (3) is expressed as follows:
![]() (4)
(4)
In this way, the gravitational force term is separated into two parts, namely Dark Matter (DM) and Dark Energy (DE) respectively. They are expressed as follows:
![]() (5)
(5)
![]() (6)
(6)
It shows that they are inverse relation to the distance![]() . And we can solve the problem about the flat rotation curves in the galaxy scales by using Equation (5) and Equation (6).
. And we can solve the problem about the flat rotation curves in the galaxy scales by using Equation (5) and Equation (6).
From the WMAP observation, it shows that the total mass of Dark Energy is more than the total mass of Dark Matter in the Universe now. But what is the mass ratio of Dark Energy to Dark Matter in the very early Universe? From the viewpoint of S. Hawking, quantum fluctuations in the very early Universe may cause incoherence between different terms in the state vector of Universe [9] [10] . It is inevitable that the quantum fluctuations dominated the Universe in the Planck scale. It indicates that the total gravity in Universe is zero which the distance ![]() is the Planck length
is the Planck length![]() . So we used the new model to calculate the total gravity to figure out the mass ratio of Dark Energy to Dark Matter in the very early Universe (see Figure 1).
. So we used the new model to calculate the total gravity to figure out the mass ratio of Dark Energy to Dark Matter in the very early Universe (see Figure 1).
As Figure 1 shows that the total gravity of Universe is zero when the ratio of Dark Energy to Dark Matter is 3:1. And it is all known to the WMAP data in 2003 that the percent of Baryons, Dark Energy and Dark Matter in the Universe is![]() ,
, ![]() and
and ![]() respectively [11] - [17] . According to our hypothesis, the same mass of Dark Matter and Dark Energy replace the same mass of Baryons in the Universe. Then, we reallocate the cosmic component which is only Dark Energy and Dark Matter. The ratio of Dark Energy
respectively [11] - [17] . According to our hypothesis, the same mass of Dark Matter and Dark Energy replace the same mass of Baryons in the Universe. Then, we reallocate the cosmic component which is only Dark Energy and Dark Matter. The ratio of Dark Energy ![]() to Dark Matter
to Dark Matter ![]() is
is![]() . It agrees with our results that the mass of Dark Energy is as three times as Dark Matter.
. It agrees with our results that the mass of Dark Energy is as three times as Dark Matter.
So giving that the mass of Dark Matter is m, the mass of Dark Energy is 3m. Taking them into Equation (4), we can get the sum of DM’s gravity and DE’s gravity, as following:
![]()
where![]() ,
, ![]() is a integral number.
is a integral number.
So we can calculate the gravity while ![]() changes from 1 to infinite (see Figure 2).
changes from 1 to infinite (see Figure 2).
![]()
Figure 1. The total gravity of Universe correspond to the mass ratio of Dark Energy (DE) to Dark Matter (DM) when r = Lp.
![]()
Figure 2. The total gravity of the Universe generated by Dark Energy and Dark Matter.
When ![]() is bigger than one, the total gravity is negative. It shows that the total gravity of Dark Energy and Dark Matter is the repulsive force. The repulsive force impels the acceleration expansion of Universe. The repulsive force decreases gradually while
is bigger than one, the total gravity is negative. It shows that the total gravity of Dark Energy and Dark Matter is the repulsive force. The repulsive force impels the acceleration expansion of Universe. The repulsive force decreases gradually while ![]() is bigger than three. With
is bigger than three. With ![]() increase, the repulsive force is approximate to zero and not equal to zero forever. It suggests that the Universe will keep expanding with the ace- leration slowing down. On the other hand, the repulsive force is the maximum value when
increase, the repulsive force is approximate to zero and not equal to zero forever. It suggests that the Universe will keep expanding with the ace- leration slowing down. On the other hand, the repulsive force is the maximum value when ![]() is equal to three. It shows that inflationary Universe is in existence as the observation improved.
is equal to three. It shows that inflationary Universe is in existence as the observation improved.
As the total Universe keep expanding, the ratio of Dark Energy to Dark Matter in the local region must deviate from 3:1. The results of simulation show that the core of our Universe is hollow now. The latter content will discuss the local gravity in the galaxy scale.
3. The Gravity Curve in the Galaxy Scales
To the different ratio of DE/DM, we use the novel interaction model to calculate a series of the local gravity in the galaxy scale (see Figure 3).
As Figure 3 shows that the sum of DE’s and DM’s gravity is always positive when the ratio of DE/DM is smaller than or equal to 1:1. The gravity curve is one branch of hyperbola and the value of the local gravity is huge in the Planck scales. It is all known that the gravity curve correspond to the characteristic property of the Solar system when the ratio of DE/DM is 1:1. The planets are limited in the stability orbits by the gravity.
The sum of DE’s and DM’s gravity is always negative when the ratio of DE/DM is larger than 3:1. It indicates that the repulsive interaction maybe keep the margin of galaxies and accompany with the Universe expansion. It agrees with the small fluctuations in the temperature of the cosmic microwave background (CMB) radiation.
When the ratio of DE/DM is larger than 1:1 and is smaller than 3:1, the sum of gravity is positive in the Planck length. It indicates that the matter in the galaxy suppress firstly and then inflate, and eventually expands. Of course, the different ratios of DE/DM correspond to the different extent. The gravity curves can describe the evolution process of different galaxies. On the other hand, the gravity falls off as ![]() when the distance
when the distance ![]() is far more than the radius of the Solar system. It can deduce the flat rotation curves of galaxy. Simultaneously, it shows that the novel interaction model can be used in the range from the galaxy scales to the Solar system by nature.
is far more than the radius of the Solar system. It can deduce the flat rotation curves of galaxy. Simultaneously, it shows that the novel interaction model can be used in the range from the galaxy scales to the Solar system by nature.
4. Conclusions
1) The paper sets up the novel interaction model based on the Newtonian law of gravity by introducing the Planck scale. It deduces the gravity formula of Dark Matter and Dark Energy, namely, the rates of change of their momentums.
2) To the early Universe, the numerical results of the novel interaction model point toward the sharp inflationary process of Universe in the Planck scales, and then Universe starts the slow expansion process that the
![]()
Figure 3. The local gravity in the galaxy scale.
acceleration velocity is slowing down forever. There is neither the suppression nor vibration in the whole process.
Simultaneously, the Newtonian law of gravity is still applicable in the Solar system.
3) The novel interaction model shows that the evolution process of the very early galaxy is divided into the
three parts: first suppress and then inflate, eventually it expands forever. Specially, the simulation shows that the core of our Universe is hollow now. But the quantity of suppression is absolute disagreement to the different kinds of galaxies, which have the different mass ratios of DE/DM.