The Numerical Solution of the MRLW Equation Using the Multigrid Method ()
1. Introduction
The numerical solution of partial differential equations requires some discretization of the domain into a collection of points. A large system of equations comes out from discretization of the same partial differential equations and the optimal method for solving these problems is multigrid method, see [1] -[9] .
Consider the following one-dimensional modified regularized long-wave (MRLW) equation: equation:
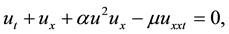(1)
where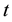 
is the time, 
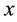is the space coordinate, 
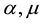are positive constants and 
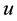is the wave amplitude with the physical boundary conditions 
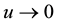as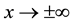
. This equation was first introduced to describe the development of an undular bore by Peregrine [10] and later by Benjamin et al. [11] . Equation (1) has various applications as in physics media since it describes the phenomena with weak nonlinearity and dispersion waves, including nonlinear transverse waves in shallow water, ion-acoustic and magneto hydrodynamic waves in plasma, and phonon packets in nonlinear crystals [11] .
Although the analytical solutions of the MRLW equation, with a limited set of boundary and initial conditions, have been existed, many authors are recently interested in the numerical solutions of this equation. Gardner et al. [12] introduced a collocation solution to the MRLW equation using quintic B-spline finite elements. Khalifa et al. [13] [14] applied the finite difference and cubic B-spline collocation finite element method to obtain the numerical solutions of the MRLW equation. Solutions based on collocation method with quadratic B-spline finite elements and the central finite difference method for time are investigated by Raslan [15] . Raslan and Hassan [16] solved the MRLW equation by a collocation finite element method using quadratic, cubic, quartic, and quintic B-spline to obtain the numerical solutions of the single solitary wave. Ali [17] has formulated a classical radial basis function collocation method for solving the MRLW equation. Haq et al. [18] have developed a numerical scheme based on quartic B-spline collocation method for the numerical solution of MRLW equation. Karakoc and Geyikli [19] solved the MRLW equation by using the Petrov-Galerkin finite element method.
An outline of this paper is as follows: we begin in Section 2 by reviewing the analytical solution of the MRLW equation. In Section 3, we derive a new numerical method based on the multigrid technique and finite difference method for obtaining the numerical solution of MRLW equation. Finally, in Section 4, we introduce the numerical results for solving the MRLW equation through some well known standard problems.
2. The Analytical Solution
The exact solution of Equation (1) can be written in the form [12] [14] :
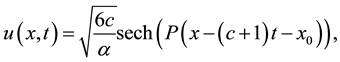(2)
which represents the motion of a single solitary wave with amplitude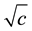
, where 
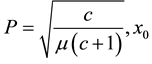and 
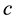
are arbitrary constants. The initial condition is given by
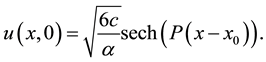(3)
The conservation properties of the MRLW equation related to mass, momentum and energy are determined by following three invariants on the region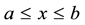
:
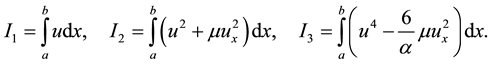(4)
3. Numerical Method
The basic idea of multigrid techniques is illustrated by Brandt [1] . In this section we apply this method for initial boundary value problem, except that, the upper boundary conditions change with time, in which the initial condition is ![]()
for![]()
. Dividing the interval of time to K parts, we obtain the solutions of the partial differential equation at time t1 and use these solutions as initial values for the next level![]()
, and for the other, we obtain the solutions at time![]()
. The numbers of points in a coarse grid for this domain are two points. We apply the full multigrid algorithm for the MRLW equation. Assuming the initial condition ![]()
and the solution![]()
, ![]()
has the usual partition with a space step size ![]()
and a time step size ![]()
![]()
. We start handling the non-linear term ![]()
by ex-
pressing in the form![]()
. The back-time and centre-space difference for Equation (1) is
![]()
(5)
where![]()
, ![]()
for a set grids ![]()
Step 1: ![]()
Step 2: Starting from ![]()
in the coarse grid, we can calculate the approximate value ![]()
at two points using Equation (5) leading to:
![]()
(6)
The right hand side for the last equation can be computed using the initial and boundary conditions.
Step 3: Interpolating the grid functions from the coarse grid to fine grid using linear interpolation![]()
, in which
![]()
(7)
that can be written explicitly as:
![]()
(8)
Step 4: Doing relaxation sweep on ![]()
using the point relaxation
![]()
(9)
Step 5: Computing the residuals ![]()
on ![]()
and inject them into ![]()
using full weighting restriction ![]()
to get ![]()
as:
![]()
(10)
![]()
(11)
Step 6: Computing an approximate solution of error![]()
.
Step 7: Interpolating the solution of error ![]()
onto![]()
, ![]()
and adding it to ![]()
which is the approximate value of ![]()
on the fine grid with![]()
.
By taking this solution on coarse grid and repeating steps 3 - 7, we obtain the approximate values of ![]()
on the grid with ![]()
and so ![]()
the final value is the solution at the time level![]()
.
Step 8:![]()
, go to step 2 (lead to the solution at higher time level as needed).
4. Numerical Results
In this section, numerical solutions of MRLW equation are obtained for standard problems as: the motion of single solitary wave, interaction of two and three solitary waves and development of Maxwellian initial condition into solitary waves. ![]()
and ![]()
error norms are used to show how good the numerical results in comparison with the exact results.
4.1. The Motion of Single Solitary Wave
Consider equation (1) with boundary conditions
![]()
(12)
and the initial condition (4).
The analytical values of the invariants of this problem can be found as [12] :
![]()
(13)
For a comparison with earlier studies [12] [13] [17] [19] we take the parameters ![]()
![]()
and ![]()
over the interval [0, 100]. To find the error norms![]()
, ![]()
and the numerical invariants ![]()
and ![]()
at various times we use the numerical solutions by applying the multigrid method up to![]()
. As reported in Table 1, the error norms![]()
, ![]()
are found to be small enough, and the computed values of invariants are in good agreement with their analytical values ![]()
![]()
Table 2 shows a comparison of the values of the invariants and error norms obtained by the present method with those obtained by other methods [12] [13] [17] [19] . It is clearly seen from Table 2 that the error norms obtained by the present method are smaller than the other methods.
4.2. Interaction of Two Solitary Waves
Consider the interaction of two separated solitary waves having different amplitudes and travelling in the same direction as a second problem. For this problem, the initial condition is given by:
![]()
(14)
where![]()
, ![]()
![]()
![]()
and ![]()
are arbitrary constants.
![]()
Table 1. Invariants and error norms for single solitary wave when![]()
.
![]()
Table 2. Comparison of errors and invariants for single solitary wave when ![]()
at![]()
.
For the computational discussion, we use parameters ![]()
![]()
and ![]()
over the rang ![]()
to coincide with those used by [19] . The experiment is run from ![]()
to ![]()
and values of the invariant quantities ![]()
and ![]()
are listed in Table 3.
Table 3 shows a comparison of the values of the invariants obtained by present method with those obtained in [19] . It is seen that the numerical values of the invariants remain almost constant during the computer run.
4.3. Interaction of Three Solitary Waves
In this section, the behavior of the interaction of three solitary waves having different amplitudes and travelling in the same direction was studied. So, we consider Equation (1) with the initial condition given by the linear sum of three well-separated solitary waves of different amplitudes:
![]()
(15)
where![]()
, ![]()
![]()
![]()
and ![]()
are arbitrary constants.
For the computational work, we used parameters ![]()
![]()
and ![]()
over the rang![]()
. The experiment is run up to time ![]()
and numerical values of the invariant quantities ![]()
and ![]()
are displayed in Table 4.
Table 4 shows a comparison of the values of the invariants obtained by the present method with those obtained in [19] . It is seen that the numerical values of the invariants remain almost constant during the computer run.
4.4. The Maxwellian Initial Condition
Finally, the development of the Maxwellian initial condition:
![]()
(16)
into a train of solitary waves is discussed. It is known that the behavior of the solution with the Maxwellian condition (16) depends on the values of![]()
. So, we study each of two cases: ![]()
and ![]()
Table 5 contains the obtained numerical values of the invariants and a comparison of the values of the invariants obtained by present method with those obtained in [19] .
![]()
Table 3. Comparison of invariants for the interaction of two solitary waves with results from [19] when ![]()
![]()
.
![]()
Table 4. Comparison of invariants for the interaction of three solitary waves with results from [19] when ![]()
![]()
.
![]()
Table 5. Invariants of MRLW equation using the Maxwellian condition.
5. Conclusion
In this work we extended the use of multigrid technique to initial boundary value problems, namely the MRLW problem. We tested our scheme through single solitary wave in which the analytic solution is known. Our scheme was extended to study the interaction of two and three solitary waves and Maxwellian initial condition where the analytic solutions are unknown during the interaction. The performance and accuracy of the method were shown by calculating the error norms![]()
, ![]()
and conservative properties of mass, momentum and energy. The computed results showed that the present scheme is a successful numerical technique for solving the MRLW problem.