Diagnosis on Surface Failure in Gear Equipment Using Time - Frequency Domain Analysis ()
1. Introduction
In order to make more progress in the gear performance, it is important to evaluate the gear dynamics more precisely, since gear is a main machine element in motion and power transmissions. For preventing the unexpected failure in mechanical systems, a large amount of work has been carried out based on a statistical model developed by Lundberg and Palmgren [1] with reliability models using the classical fatigue theory. However, most of these works did not consider the operating conditions of machine during the fatigue process.
Generally, the gear dynamic performance has been analyzed using Fast Fourier Transform (FFT) as a function of frequency. However, it is difficult to identify an instantaneous change of signals. In many health monitoring applications, it is more useful to analyze how measurement characteristics change as a function of both time and frequency. The Wavelet Transform (WT) is a method for the time-frequency analysis of signals [2,3]. The WT involves decomposing a signal into a representation comprised of local basis functions called wavelets. Each wavelet is located at a different position on the time axis and is local in the sense that it decays to zero when sufficiently far away from its center. The structure of a non-stationary signal can be analyzed in this way with local features represented by closely-packed wavelets of short length. Therefore, the WT can provide more beneficial information about the frequency compared with the FFT. By reason of the advantage on the WT, the applications of the WT to the diagnostics of the gear sets have been studied [4-7]. Their studies have focused mainly on whether some kinds of the WTs can provide the information to detect the fault of the gear system. However, it is also important to diagnose the failure of the gear sets using not only the WT but also the tooth meshing of the gear pair. Considering the tooth meshing of the gear pair would enable to construct the new diagnosis for the gear sets, which is different from the conventional diagnosis.
In order to evaluate the dynamic characteristics of gear pair, the dynamic performance of sintered and steel gears were measured using a power circulating gear testing machine. The dynamic characteristics were analyzed in a time-frequency domain by the continuous WT, and also those signals were decomposed and reconstructed by the discrete WT. The validity of the new evaluation method by the WT was discussed. Furthermore, in order to perform the health monitoring of the gear sets, a gear fatigue test was carried out and the dynamic characteristics during the fatigue test were measured and discussed by using the WT.
2. Wavelet Transform
The Wavelet Transform (WT) has been extensively developed. Applications of the WT are actively studied in a variety of fields in engineering [4-9]. The Continuous Wavelet Transform (CWT) of a function f(t) is defined as follows.
(1)
where, the bar over ψ(t) indicates the conjugate of a mother wavelet function ψ(t), a and b indicate the parameters on frequency and time. The Gabor function defined by Equation (2) is adopted as the wavelet function ψ(t).
(2)
where, ωp is a center of angular frequency, γ is a constant and was set at 
= 5.336 in this study. Figure 1 shows Gabor function based on sinusoidal waves eiωt and its Fourier spectrum.
When the coordinates (b, a) of the CWT shown in Equation (1) are discretized to the coordinates (2-j k, 2-j) using two integers j and k, the Discrete Wavelet Transform (DWT) is defined as follows.
(3)
where, 
is equal to (Wψ f)(2-jk, 2-j). j is called level. The Inverse Discrete Wavelet Transform (IDWT) is defined as
(4)
The function gj(t) on the wavelet component is given by
(5)
Suppose that fj(t) is the function at a level j, fj(t) is satisfied with the following relation.
(6)
where, 
is a sequence at a level j, and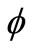 
(t) is a scaling function. The scaling function 
(t) and the mother wavelet function ψ(t) are satisfied with the two-scale relations as follows.
(7)
(8)
where, {pk} and {qk} are two-scale sequences. The functions gj(t) and fj(t) at a level j are able to be found by using Equations (5) and (6). The function fj(t) decomposed into the function gj(t) on the wavelet component is satisfied with the following relation.
(9)
In this study, the scaling and the mother wavelet functions based on the cardinal B-spline function in order of m = 4 was adopted. The cardinal B-spline function Nm(t) in order of m is defined as follows.
(10)
Figure 2 shows the scaling function 
(t) and the mother wavelet function ψ(t) based on the function N4(t). The sequences {ak}, {bk}, {pk} and {qk} are given in Reference [2].
3. Dynamic Characteristics of Gear
3.1. Test Gear and Testing Machine
Table 1 shows the specifications of gear pair employed in this dynamic performance test. The module is 5 mm and the pressure angle is 20 deg. The test gears are